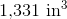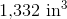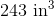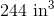Solve Problems Involving Area, Volume and Surface Area of Two- and Three-Dimensional Objects: CCSS.Math.Content.7.G.B.6
Help Questions
7th Grade Math › Solve Problems Involving Area, Volume and Surface Area of Two- and Three-Dimensional Objects: CCSS.Math.Content.7.G.B.6
The length of the side of a cube is 

Explanation
Substitute 

What is the area of the triangle pictured above?
12
24
30
40
60
Explanation
The area of a triangle is calculated using the formula 

Calculate the volume of the provided figure.

Explanation
In order to solve this problem, we need to recall the volume formula for a cube:
Now that we have the correct formula, we can substitute in our known values and solve:
The length of the side of a cube is 

Explanation
Substitute 
If a cube has one side measuring 
Explanation
To find the surface area of a cube, use the formula 




Calculate the area of the provided figure.

Explanation
In order to solve this problem, we need to recall the area formula for a circle:
Now that we have the correct formula, we can substitute in our known values and solve:
Calculate the area of the provided figure.

Explanation
In order to solve this problem, we need to recall the area formula for a circle:
Now that we have the correct formula, we can substitute in our known values and solve:
If a cube has one side measuring 
Explanation
To find the surface area of a cube, use the formula 




Calculate the volume of the provided figure.

Explanation
In order to solve this problem, we need to recall the volume formula for a rectangular prism:
Now that we have the correct formula, we can substitute in our known values and solve:

What is the area of the triangle pictured above?
12
24
30
40
60
Explanation
The area of a triangle is calculated using the formula