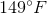Solve Word Problems Leading to Equations: CCSS.Math.Content.7.EE.B.4a
Help Questions
7th Grade Math › Solve Word Problems Leading to Equations: CCSS.Math.Content.7.EE.B.4a
If a rectangle possesses a width of 

Explanation
In order to solve this problem, we need to recall the formula for perimeter of a rectangle:
We can substitute in our known values and solve for our unknown variable (i.e. length):
We want to isolate the 

Next, we can divide each side by
The length of the rectangle is
If a rectangle possesses a width of 

Explanation
In order to solve this problem, we need to recall the formula for perimeter of a rectangle:
We can substitute in our known values and solve for our unknown variable (i.e. length):
We want to isolate the 

Next, we can divide each side by
The length of the rectangle is
If a rectangle possesses a width of 

Explanation
In order to solve this problem, we need to recall the formula for perimeter of a rectangle:
We can substitute in our known values and solve for our unknown variable (i.e. length):
We want to isolate the 

Next, we can divide each side by
The length of the rectangle is
Gary is twice as old as his niece Candy. How old will Candy will be in five years when Gary is 
Not enough information is given to determine the answer.
Explanation
Since Gary will be 37 in five years, he is 


If a rectangle possesses a width of 

Explanation
In order to solve this problem, we need to recall the formula for perimeter of a rectangle:
We can substitute in our known values and solve for our unknown variable (i.e. length):
We want to isolate the 

Next, we can divide each side by
The length of the rectangle is
If a rectangle possesses a width of 

Explanation
In order to solve this problem, we need to recall the formula for perimeter of a rectangle:
We can substitute in our known values and solve for our unknown variable (i.e. length):
We want to isolate the 

Next, we can divide each side by
The length of the rectangle is
Let 

What is 
Explanation
Let 

What is 
Explanation

Write as an equation:
Twice the sum of a number and ten is equal to the difference of the number and one half.
Explanation
Let 
"The sum of a number and ten" is the expression 

"The difference of the number and one half" is a subtraction of the two, or
Set these equal, and the desired equation is
Write as an equation:
Five-sevenths of the difference of a number and nine is equal to forty.
Explanation
"The difference of a number and nine" is the result of a subtraction of the two, so we write this as
"Five-sevenths of" this difference is the product of 
This is equal to forty, so write the equation as








![\frac{\begin{array}[b]{r}18=2l+4\ -4\ \ \ \ \ \ -4\end{array}}{\\14=2l}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/924412/gif.latex)

![\frac{\begin{array}[b]{r}\frac{14}{2}=\frac{2l}{2}\\end{array}}{7=l}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/924413/gif.latex)








![\frac{\begin{array}[b]{r}36=2l+16\ -16\ \ \ \ \ \ -16\end{array}}{\\20=2l}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/924152/gif.latex)
![\frac{\begin{array}[b]{r}\frac{20}{2}=\frac{2l}{2}\\end{array}}{10=l}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/924154/gif.latex)








![\frac{\begin{array}[b]{r}50=2l+22\ -22\ \ \ \ \ \ -22\end{array}}{\\28=2l}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/924303/gif.latex)
![\frac{\begin{array}[b]{r}\frac{28}{2}=\frac{2l}{2}\\end{array}}{14=l}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/924304/gif.latex)












![\frac{\begin{array}[b]{r}36=2l+24\ -24\ \ \ \ \ \ -24\end{array}}{\\12=2l}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/924287/gif.latex)
![\frac{\begin{array}[b]{r}\frac{12}{2}=\frac{2l}{2}\\end{array}}{6=l}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/924288/gif.latex)








![\frac{\begin{array}[b]{r}48=2l+18\ -18\ \ \ \ \ \ -18\end{array}}{\\30=2l}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/924311/gif.latex)
![\frac{\begin{array}[b]{r}\frac{30}{2}=\frac{2l}{2}\\end{array}}{15=l}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/924312/gif.latex)