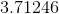An irrational number is any number that cannot be written as a fraction of whole numbers. The number pi and square roots of non-perfect squares are examples of irrational numbers.

can be written as the fraction . The term is a whole number. The square root of is , also a rational number. , however, is not a perfect square, and its square root, therefore, is irrational.

Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers.

Rational numbers are numbers that we use most often, and can be written as a simple fraction.

Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end.

In this case, is our only irrational number because it cannot be written as a simple fraction.

An irrational number is any number that can not be expressed as a ratio of integers, i.e. a fraction. Therefore, the only irrational number listed is .

The definition of an irrational number is a number which cannot be expressed in a simple fraction, or a number that is not rational.

Using the above definition, we see that is already expressed as a simple fraction.

any number and

. All of these options can be expressed as simple fractions, making them all rational numbers, and the incorrect answers.

cannot be expressed as a simple fraction and is equal to a non-terminating, non-repeating (ever-changing) decimal, begining with

This is an irrational number and our correct answer.

An irrational number cannot be represented as the quotient of two integers.

Irrational numbers do not terminate and are not repeat numbers.

Looking at the possible answers,

can be reduced to , therefore it is an integer.

by definition is a quotient of two integers and thus it is not an irrational number.

can be rewritten as and by definition is a quotient of two integers and thus it is not an irrational number.

is a terminated decimal and therefore can be written as a fraction. Thus it is not an irrational number.

is the number for and does not terminate, therefore it is irrational.

Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers.

Rational numbers are numbers that we use most often, and can be written as a simple fraction.

Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end.

In this case, is our only irrational number because it cannot be written as a simple fraction.

Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers.

Rational numbers are numbers that we use most often, and can be written as a simple fraction.

Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end.

In this case, is our only irrational number because it cannot be written as a simple fraction.

Rational numbers are those which can be written as a ratio of two integers, or simply, as a fraction.

The solution of is , which can be written as . Each of the other answers would have a solution with an infinite number of decimal points, and therefore cannot be written as a simple ratio. They are irrational numbers.

Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers.

Rational numbers are numbers that we use most often, and can be written as a simple fraction.

Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end.

In this case, is our only rational number because it is written as a simple fraction:

A rational number is any number that can be expressed as a fraction/ratio, with both the numerator and denominator being integers. The one limitation to this definition is that the denominator cannot be equal to .

Using the above definition, we see , and (which is ) cannot be expressed as fractions. These are non-terminating numbers that are not repeating, meaning the decimal has no pattern and constantly changes. When a decimal is non-terminating and constantly changes, it cannot be expressed as a fraction.

is the correct answer because , which can be expressed as , fullfilling our above defintion of a rational number.