Fractions - ACT Math
Card 0 of 2070
What common number can you add to the numerator and denominator of  to get
to get  ?
?
What common number can you add to the numerator and denominator of 

Set up an equation where you add the same unknown number (x) to both the numerator and the denominator of the original fraction, and set the equation equal to  .
.

Cross-multiply the fractions to simplify.


Now, solve for x.




Set up an equation where you add the same unknown number (x) to both the numerator and the denominator of the original fraction, and set the equation equal to 
Cross-multiply the fractions to simplify.
Now, solve for x.
Compare your answer with the correct one above
Solve for x where

Solve for x where
To solve this, subtract 1 1/2 from both sides. Convert to common denominators.
4 1/3 – 1 1/2 = 4 2/6 – 1 3/6.
In order to subtract, you'll want to "borrow" from the 4 2/6. Rewrite 4 2/6 as 3 8/6 and then subtract 1 3/6 from this. Your solution is 2 5/6. Most calculators will also do these calculations for you.
To solve this, subtract 1 1/2 from both sides. Convert to common denominators.
4 1/3 – 1 1/2 = 4 2/6 – 1 3/6.
In order to subtract, you'll want to "borrow" from the 4 2/6. Rewrite 4 2/6 as 3 8/6 and then subtract 1 3/6 from this. Your solution is 2 5/6. Most calculators will also do these calculations for you.
Compare your answer with the correct one above
Choose the answer which best solves the equation below:

Choose the answer which best solves the equation below:
To solve this equation, you must first make sure that both fractions have a common denominator.
In this case the common denominator will be 12:

Then you perform your operation:



To solve this equation, you must first make sure that both fractions have a common denominator.
In this case the common denominator will be 12:
Then you perform your operation:
Compare your answer with the correct one above
If John has  slices of an
slices of an  slice pizza left over, and he eats
slice pizza left over, and he eats  of them, what fraction of the pizza does he have left over?
of them, what fraction of the pizza does he have left over?
If John has 


To find this answer, first you need to set up your equation:

And you need to get rid of the decimal in the numerator. We can do this by multiplying each fraction by 2/2.


Then solve for your answer:

To find this answer, first you need to set up your equation:
And you need to get rid of the decimal in the numerator. We can do this by multiplying each fraction by 2/2.
Then solve for your answer:
Compare your answer with the correct one above
Solve for  :
:

Solve for 

Begin by isolating your variable:

Next, you need to find the common denominator. For the left side of your equation, it is  . For the right, it is
. For the right, it is  . This means that you need to rewrite as follows:
. This means that you need to rewrite as follows:

Now, simplify and combine terms:


You can further simplify the left side:

Next, multiply both sides by  . This gives you:
. This gives you:

Begin by isolating your variable:
Next, you need to find the common denominator. For the left side of your equation, it is 

Now, simplify and combine terms:
You can further simplify the left side:
Next, multiply both sides by 
Compare your answer with the correct one above
Simplify:

Simplify:
First, you must convert your fractions to the common denominator of  :
:

Next, do your subtraction:

Next, you must be very careful. Notice how you must handle your subtractions in order to maintain the correct distribution of signs:

Now, carefully distribute for each group:

Next, simplify:

Factor out the common  in the numerator:
in the numerator:

There is still a common  , but that does not help you get your fraction into the form found in the answers.
, but that does not help you get your fraction into the form found in the answers.
First, you must convert your fractions to the common denominator of 
Next, do your subtraction:
Next, you must be very careful. Notice how you must handle your subtractions in order to maintain the correct distribution of signs:
Now, carefully distribute for each group:
Next, simplify:
Factor out the common 
There is still a common 
Compare your answer with the correct one above
Convert the following to a percentage.

Convert the following to a percentage.
To convert a fraction into a percentage, simply simplify the fraction into a decimal and multiply by 100.
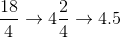

To convert a fraction into a percentage, simply simplify the fraction into a decimal and multiply by 100.
Compare your answer with the correct one above
The girl's tennis team decided to do multiple fundraisers to raise enough to buy new equipment for next season. The following is a table of 4 of the fundraisers they did and the fraction of the total funds each raised.

The last fundraiser they did earned them the final  they needed. What percent of the total funds raised did the last fundraiser raise?
they needed. What percent of the total funds raised did the last fundraiser raise?
The girl's tennis team decided to do multiple fundraisers to raise enough to buy new equipment for next season. The following is a table of 4 of the fundraisers they did and the fraction of the total funds each raised.
The last fundraiser they did earned them the final 
The question asks to find what percent the last fundraiser makes up of the total funds raised. The information that's given is how much that last fundraiser made and what fraction the other fundraisers made.
This problem may be solved without the amount of money the last fundraiser raised. The reason is that we know that only 5 fundraisers were done. We're given what the fraction of the other fundraisers were.
If we were to add all the fractions together, including the last fundraiser, the sum of all would equal 1.

Fractions are another version of decimals but also another version of percentages. Percentages are essentially a prettier way of showing parts (or fractions) of a whole, which would be 100%. In the case of fractions, this is the same logic, which is why when all the fractions are summed, they equal 1. This 1 represents 100%.
Upon using lowest common denominators, adding the fractions together, and solving for x, x is calculated to be 
We've almost obtained the final answer. Now it's just a matter of converting this fraction into a percent. As mentioned previously, fractions are another version of decimals. Think of decimals as being the middle conversion between fractions and percents. All that needs to be done to a decimal to turn it in to a percent is to multiply it by 100. For instance, .50 becomes 50%. Conversely, .50 is the same as  in fraction form. Therefore, one half is 50%.
in fraction form. Therefore, one half is 50%.
In order to solve for x in percent, the same conversion must be done.


The question asks to find what percent the last fundraiser makes up of the total funds raised. The information that's given is how much that last fundraiser made and what fraction the other fundraisers made.
This problem may be solved without the amount of money the last fundraiser raised. The reason is that we know that only 5 fundraisers were done. We're given what the fraction of the other fundraisers were.
If we were to add all the fractions together, including the last fundraiser, the sum of all would equal 1.
Fractions are another version of decimals but also another version of percentages. Percentages are essentially a prettier way of showing parts (or fractions) of a whole, which would be 100%. In the case of fractions, this is the same logic, which is why when all the fractions are summed, they equal 1. This 1 represents 100%.
Upon using lowest common denominators, adding the fractions together, and solving for x, x is calculated to be
We've almost obtained the final answer. Now it's just a matter of converting this fraction into a percent. As mentioned previously, fractions are another version of decimals. Think of decimals as being the middle conversion between fractions and percents. All that needs to be done to a decimal to turn it in to a percent is to multiply it by 100. For instance, .50 becomes 50%. Conversely, .50 is the same as 
In order to solve for x in percent, the same conversion must be done.
Compare your answer with the correct one above
If a dress in a store originally costs  , what does it cost (in dollars) after a
, what does it cost (in dollars) after a  discount is applied?
discount is applied?
If a dress in a store originally costs 

To find  of 80,
of 80,  . Next, subtract
. Next, subtract  , for
, for  as the final answer.
as the final answer.
To find 



Compare your answer with the correct one above
A wedding planner knows she must deliver 85 small fruits and 40 large fruits to the wedding event. She knows that one basket can hold either 5 small fruits or 3 large fruits. What is the minimum number of baskets she must bring to the event to fulfill their demand?
A wedding planner knows she must deliver 85 small fruits and 40 large fruits to the wedding event. She knows that one basket can hold either 5 small fruits or 3 large fruits. What is the minimum number of baskets she must bring to the event to fulfill their demand?
To know the minumum number of baskets required for each size, simply divide the number of fruits required by the basket capacity for each fruit:

 (we must round up to nearest whole number for practical purposes)
(we must round up to nearest whole number for practical purposes)
Since we need to bring both the large and small fruits to the event, we need to add these two values:  baskets total.
baskets total.
To know the minumum number of baskets required for each size, simply divide the number of fruits required by the basket capacity for each fruit:

Since we need to bring both the large and small fruits to the event, we need to add these two values: 
Compare your answer with the correct one above
After saving her money for six weeks, Felicia has saved up  . If she saves three-fifths of her pay each week, how much does she make in a week?
. If she saves three-fifths of her pay each week, how much does she make in a week?
After saving her money for six weeks, Felicia has saved up 
When working with fractions or percents, it is often really helpful to write out an equation showing what you need to find. In this case, we know that three-fifths of Felicia's weekly pay (our variable—let's call it  ) over six weeks results in
) over six weeks results in  , so our equation looks like this:
, so our equation looks like this:

So, we want to simplify and rearrange this equation. Start by multiplying the  with the
with the  :
:

Then, multiply both sides by  , the reciprocal of
, the reciprocal of  :
:

So,  , and we now know Felicia's weekly pay!
, and we now know Felicia's weekly pay!
When working with fractions or percents, it is often really helpful to write out an equation showing what you need to find. In this case, we know that three-fifths of Felicia's weekly pay (our variable—let's call it 

So, we want to simplify and rearrange this equation. Start by multiplying the 

Then, multiply both sides by 

So, 
Compare your answer with the correct one above
A company needs 45 pounds of apples to make 30 containers of apple juice. How many pounds of apples would the company need to make 20 containers of apple juice?
A company needs 45 pounds of apples to make 30 containers of apple juice. How many pounds of apples would the company need to make 20 containers of apple juice?
To answer this question, we need to set up a proportion for how many pounds of apples it takes to make a certain number of containers, knowing that 45 pounds of apples makes 30 containers of apple juice. We want to figure out how many pounds of apples it would take to make 20 containers of apple juice.
To set up a proportion, we must put the amounts that correspond to each other in the same fraction and equate it to a similar fraction. In this case, we will set up fractions that show containers of apple juice over pounds of apples. So for this data:

Note that we put both of the values for containers of apple juice in the numerator of the fractions and pounds of apples in the denominator. Here,  is the value we are looking for.
is the value we are looking for.
We then cross-multiply by taking the denominator of each fraction and multiplying each side of the equation by it so that we can create an equation that is solved easier.




Therefore, it takes  pounds of apples to make
pounds of apples to make  containers of apple juice.
containers of apple juice.
To answer this question, we need to set up a proportion for how many pounds of apples it takes to make a certain number of containers, knowing that 45 pounds of apples makes 30 containers of apple juice. We want to figure out how many pounds of apples it would take to make 20 containers of apple juice.
To set up a proportion, we must put the amounts that correspond to each other in the same fraction and equate it to a similar fraction. In this case, we will set up fractions that show containers of apple juice over pounds of apples. So for this data:
Note that we put both of the values for containers of apple juice in the numerator of the fractions and pounds of apples in the denominator. Here, 
We then cross-multiply by taking the denominator of each fraction and multiplying each side of the equation by it so that we can create an equation that is solved easier.
Therefore, it takes 

Compare your answer with the correct one above
If  ,
, 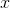 can equal which of the following?
can equal which of the following?
If 
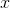
Convert all of the fractions to decimals. Thus, x is contained within the range of 0.33 < x < 0.76. The answers choices become 1/4 = 0.25, 4/12 = 0.33, 2/5 = 0.4, and 5/16 = 0.3125, respectively. Therefore, the only answer which is within the desired range is 2/5.
Convert all of the fractions to decimals. Thus, x is contained within the range of 0.33 < x < 0.76. The answers choices become 1/4 = 0.25, 4/12 = 0.33, 2/5 = 0.4, and 5/16 = 0.3125, respectively. Therefore, the only answer which is within the desired range is 2/5.
Compare your answer with the correct one above
Find the sum of the following:

Find the sum of the following:
To get the decimal from a fraction, divide the numerator by the denominator





To get the decimal from a fraction, divide the numerator by the denominator
Compare your answer with the correct one above
When 5/11 is written as a decimal, what is the 100th digit to the right of the decimal point?
When 5/11 is written as a decimal, what is the 100th digit to the right of the decimal point?
When 5 is divided by 11, the decimal is 0.45 repeating, with a 5 in the hundreths place. The key here is to recognize that 100 is an even number, and the 5 in 0.45 is two places to the right of the decimal point (2 also being an even number).
When 5 is divided by 11, the decimal is 0.45 repeating, with a 5 in the hundreths place. The key here is to recognize that 100 is an even number, and the 5 in 0.45 is two places to the right of the decimal point (2 also being an even number).
Compare your answer with the correct one above
Find the sum to the nearest hundredth:

Find the sum to the nearest hundredth:
1. Convert the fractions to decimals by division:


2. Add the corresponding whole numbers to the decimals:


3. Add the two decimals:

1. Convert the fractions to decimals by division:
2. Add the corresponding whole numbers to the decimals:
3. Add the two decimals:
Compare your answer with the correct one above
A pie is made up of  crust,
crust,  apples, and
apples, and  sugar, and the rest is jelly. What is the ratio of crust to jelly?
sugar, and the rest is jelly. What is the ratio of crust to jelly?
A pie is made up of 


A pie is made up of  crust,
crust,  apples,
apples,  sugar, and the rest is jelly. What is the ratio of crust to jelly?
sugar, and the rest is jelly. What is the ratio of crust to jelly?
To compute this ratio, you must first ascertain how much of the pie is jelly. This is:

Begin by using the common denominator  :
:


So, the ratio of crust to jelly is:

This can be written as the fraction:
 , or
, or 
A pie is made up of 


To compute this ratio, you must first ascertain how much of the pie is jelly. This is:
Begin by using the common denominator 
So, the ratio of crust to jelly is:
This can be written as the fraction:

Compare your answer with the correct one above
In a solution,  of the fluid is water,
of the fluid is water,  is wine, and
is wine, and  is lemon juice. What is the ratio of lemon juice to water?
is lemon juice. What is the ratio of lemon juice to water?
In a solution, 


This problem is really an easy fraction division. You should first divide the lemon juice amount by the water amount:

Remember, to divide fractions, you multiply by the reciprocal:

This is the same as saying:

This problem is really an easy fraction division. You should first divide the lemon juice amount by the water amount:
Remember, to divide fractions, you multiply by the reciprocal:
This is the same as saying:
Compare your answer with the correct one above
If  and
and  , what is the ratio of
, what is the ratio of  to
to  ?
?
If 



To find a ratio like this, you simply need to make the fraction that represents the division of the two values by each other. Therefore, we have:

Recall that division of fractions requires you to multiply by the reciprocal:
 ,
,
which is the same as:

This is the same as the ratio:

To find a ratio like this, you simply need to make the fraction that represents the division of the two values by each other. Therefore, we have:
Recall that division of fractions requires you to multiply by the reciprocal:

which is the same as:
This is the same as the ratio:
Compare your answer with the correct one above
What is the average of  and
and  ?
?
What is the average of 

To average, we have to add the values and divide by two. To do this we need to find a common denomenator of 6. We then add and divide by 2, yielding 4.5/6. This reduces to 3/4.
To average, we have to add the values and divide by two. To do this we need to find a common denomenator of 6. We then add and divide by 2, yielding 4.5/6. This reduces to 3/4.
Compare your answer with the correct one above






