Complex Fractions - ACT Math
Card 0 of 225
Simplify 
Simplify
Simplify the complex fraction by multiplying by the complex denominator:
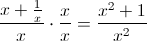
Simplify the complex fraction by multiplying by the complex denominator:
Compare your answer with the correct one above
Steven purchased 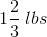 of vegetables on Monday and
of vegetables on Monday and  of vegetables on Tuesday. What was the total weight, in pounds, of vegetables purchased by Steven?
of vegetables on Tuesday. What was the total weight, in pounds, of vegetables purchased by Steven?
Steven purchased 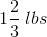

To solve this answer, we have to first make the mixed numbers improper fractions so that we can then find a common denominator. To make a mixed number into an improper fraction, you multiply the denominator by the whole number and add the result to the numerator. So, for the presented data:

and

Now, to find out how many total pounds of vegetables Steven purchased, we need to add these two improper fractions together:
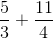
To add these fractions, they need to have a common denominator. We can adjust each fraction to have a common denominator of  by multiplying
by multiplying  by
by  and
and  by
by  :
:

To multiply fractions, just multiply across:

We can now add the numerators together; the denominator will stay the same:

Since all of the answer choices are mixed numbers, we now need to change our improper fraction answer into a mixed number answer. We can do this by dividing the numerator by the denominator and leaving the remainder as the numerator:


This means that our final answer is 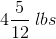 .
.
To solve this answer, we have to first make the mixed numbers improper fractions so that we can then find a common denominator. To make a mixed number into an improper fraction, you multiply the denominator by the whole number and add the result to the numerator. So, for the presented data:
and
Now, to find out how many total pounds of vegetables Steven purchased, we need to add these two improper fractions together:
To add these fractions, they need to have a common denominator. We can adjust each fraction to have a common denominator of 




To multiply fractions, just multiply across:
We can now add the numerators together; the denominator will stay the same:
Since all of the answer choices are mixed numbers, we now need to change our improper fraction answer into a mixed number answer. We can do this by dividing the numerator by the denominator and leaving the remainder as the numerator:
This means that our final answer is 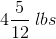
Compare your answer with the correct one above
Simplify 
Simplify
Simplify the complex fraction by multiplying by the complex denominator:
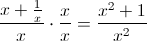
Simplify the complex fraction by multiplying by the complex denominator:
Compare your answer with the correct one above
Steven purchased 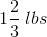 of vegetables on Monday and
of vegetables on Monday and  of vegetables on Tuesday. What was the total weight, in pounds, of vegetables purchased by Steven?
of vegetables on Tuesday. What was the total weight, in pounds, of vegetables purchased by Steven?
Steven purchased 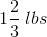

To solve this answer, we have to first make the mixed numbers improper fractions so that we can then find a common denominator. To make a mixed number into an improper fraction, you multiply the denominator by the whole number and add the result to the numerator. So, for the presented data:

and

Now, to find out how many total pounds of vegetables Steven purchased, we need to add these two improper fractions together:
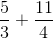
To add these fractions, they need to have a common denominator. We can adjust each fraction to have a common denominator of  by multiplying
by multiplying  by
by  and
and  by
by  :
:

To multiply fractions, just multiply across:

We can now add the numerators together; the denominator will stay the same:

Since all of the answer choices are mixed numbers, we now need to change our improper fraction answer into a mixed number answer. We can do this by dividing the numerator by the denominator and leaving the remainder as the numerator:


This means that our final answer is 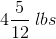 .
.
To solve this answer, we have to first make the mixed numbers improper fractions so that we can then find a common denominator. To make a mixed number into an improper fraction, you multiply the denominator by the whole number and add the result to the numerator. So, for the presented data:
and
Now, to find out how many total pounds of vegetables Steven purchased, we need to add these two improper fractions together:
To add these fractions, they need to have a common denominator. We can adjust each fraction to have a common denominator of 




To multiply fractions, just multiply across:
We can now add the numerators together; the denominator will stay the same:
Since all of the answer choices are mixed numbers, we now need to change our improper fraction answer into a mixed number answer. We can do this by dividing the numerator by the denominator and leaving the remainder as the numerator:
This means that our final answer is 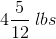
Compare your answer with the correct one above
Which of the following is equal to  ?
?
Which of the following is equal to 
First we must take the numerator of our whole problem. There is a fraction in the numerator with  as the denominator. Therefore, we multiply the numerator of our whole problem by
as the denominator. Therefore, we multiply the numerator of our whole problem by  , giving us
, giving us  .
.
Now we look at the denominator of the whole problem, and we see that there is another fraction present with  as a denominator. So now, we multiply the denominator by
as a denominator. So now, we multiply the denominator by  , giving us
, giving us  .
.
Our fraction should now read  . Now, we can factor our denominator, making the fraction
. Now, we can factor our denominator, making the fraction  .
.
Finally, we cancel out  from the top and the bottom, giving us
from the top and the bottom, giving us  .
.
First we must take the numerator of our whole problem. There is a fraction in the numerator with 


Now we look at the denominator of the whole problem, and we see that there is another fraction present with 


Our fraction should now read 

Finally, we cancel out 

Compare your answer with the correct one above
Simplify: 
Simplify:
Rewrite  into the following form:
into the following form:

Change the division sign to a multiplication sign by flipping the 2nd term and simplify.

Rewrite 
Change the division sign to a multiplication sign by flipping the 2nd term and simplify.
Compare your answer with the correct one above
Evaluate: 
Evaluate:
The expression  can be rewritten as:
can be rewritten as:

Change the division sign to a multiplication sign and take the reciprocal of the second term. Evaluate.

The expression 
Change the division sign to a multiplication sign and take the reciprocal of the second term. Evaluate.
Compare your answer with the correct one above
Simplify: 
Simplify:
The expression  can be simplified as follows:
can be simplified as follows:
We can simplify each fraction by multiplying the numerator by the reciprocal of the denominator.


From here we add our two new fractions together and simplify.

The expression 
We can simplify each fraction by multiplying the numerator by the reciprocal of the denominator.
From here we add our two new fractions together and simplify.
Compare your answer with the correct one above
Simplify the following:

Simplify the following:
Begin by simplifying your numerator. Thus, find the common denominator:

Next, combine the fractions in the numerator:

Next, remember that to divide fractions, you multiply the numerator by the reciprocal of the denominator:

Since nothing needs to be simplified, this is just:

Begin by simplifying your numerator. Thus, find the common denominator:
Next, combine the fractions in the numerator:
Next, remember that to divide fractions, you multiply the numerator by the reciprocal of the denominator:
Since nothing needs to be simplified, this is just:
Compare your answer with the correct one above
Simplify,

Simplify,
Convert the numerators and denominators into single fractions, then simplify.
Start by finding the lowest common denominator in both the numerator and denominator of the complex fraction.



Add fractions with like denominators.

Simplify. Divide complex fractions by multiplying the numerator by the reciprocal of the denominator.

Solve.

Convert the numerators and denominators into single fractions, then simplify.
Start by finding the lowest common denominator in both the numerator and denominator of the complex fraction.
Add fractions with like denominators.
Simplify. Divide complex fractions by multiplying the numerator by the reciprocal of the denominator.
Solve.
Compare your answer with the correct one above
Subtract: 
Subtract:
The least common multiple can be found by multiplying the denominators: 2, 3, and 5. The common denominator of these numbers is 30. Multiply the numerator with what was multiplied to the denominator of each term, and then solve.



The least common multiple can be found by multiplying the denominators: 2, 3, and 5. The common denominator of these numbers is 30. Multiply the numerator with what was multiplied to the denominator of each term, and then solve.
Compare your answer with the correct one above
What is  ?
?
What is 
First, simplify both sides.  becomes
becomes  and
and  becomes
becomes  . The LCF between
. The LCF between  and
and  is 36. Thus,
is 36. Thus,  This simplifies to
This simplifies to  .
.
First, simplify both sides. 







Compare your answer with the correct one above
Simplify:

Simplify:
Begin by simplifying the denominator of the first fraction:

Now, remember that division of fractions is done by multiplying the numerator by the reciprocal of the denominator. Thus:

Simplify a bit:

Begin by simplifying the denominator of the first fraction:
Now, remember that division of fractions is done by multiplying the numerator by the reciprocal of the denominator. Thus:
Simplify a bit:
Compare your answer with the correct one above
Calculate

Calculate
To add complex fractions, convert the numerators and denominators into single fractions, then simplify.
Start by finding the lowest common denominator in both the numerator and denominator of the complex fraction.



Add fractions with like denominators.

Simplify. Divide complex fractions by multiplying the numerator by the reciprocal of the denominator.

Solve.

To add complex fractions, convert the numerators and denominators into single fractions, then simplify.
Start by finding the lowest common denominator in both the numerator and denominator of the complex fraction.
Add fractions with like denominators.
Simplify. Divide complex fractions by multiplying the numerator by the reciprocal of the denominator.
Solve.
Compare your answer with the correct one above
Calculate

Calculate
To add complex fractions, convert the numerators and denominators into single fractions, then simplify.
Start by finding the lowest common denominator in both the numerator and denominator of the complex fraction.



Add fractions with like denominators.

Simplify. Divide complex fractions by multiplying the numerator by the reciprocal of the denominator.

Solve.

To add complex fractions, convert the numerators and denominators into single fractions, then simplify.
Start by finding the lowest common denominator in both the numerator and denominator of the complex fraction.
Add fractions with like denominators.
Simplify. Divide complex fractions by multiplying the numerator by the reciprocal of the denominator.
Solve.
Compare your answer with the correct one above
Calculate

Calculate
To add complex fractions, convert the numerators and denominators into single fractions, then simplify.
Start by finding the lowest common denominator in both the numerator and denominator of the complex fraction.



Add fractions with like denominators.

Simplify. Divide complex fractions by multiplying the numerator by the reciprocal of the denominator.

Solve.

To add complex fractions, convert the numerators and denominators into single fractions, then simplify.
Start by finding the lowest common denominator in both the numerator and denominator of the complex fraction.
Add fractions with like denominators.
Simplify. Divide complex fractions by multiplying the numerator by the reciprocal of the denominator.
Solve.
Compare your answer with the correct one above
Calculate

Calculate
To add complex fractions, convert the numerators and denominators into single fractions, then simplify.
Start by finding the lowest common denominator in both the numerator and denominator of the complex fraction.



Add fractions with like denominators.

Simplify. Divide complex fractions by multiplying the numerator by the reciprocal of the denominator.

Solve.

To add complex fractions, convert the numerators and denominators into single fractions, then simplify.
Start by finding the lowest common denominator in both the numerator and denominator of the complex fraction.
Add fractions with like denominators.
Simplify. Divide complex fractions by multiplying the numerator by the reciprocal of the denominator.
Solve.
Compare your answer with the correct one above
Calculate

Calculate
To add complex fractions, convert the numerators and denominators into single fractions, then simplify.
Start by finding the lowest common denominator in both the numerator and denominator of the complex fraction.



Add fractions with like denominators.

Simplify. Divide complex fractions by multiplying the numerator by the reciprocal of the denominator.

Solve.

To add complex fractions, convert the numerators and denominators into single fractions, then simplify.
Start by finding the lowest common denominator in both the numerator and denominator of the complex fraction.
Add fractions with like denominators.
Simplify. Divide complex fractions by multiplying the numerator by the reciprocal of the denominator.
Solve.
Compare your answer with the correct one above
Calculate

Calculate
To add complex fractions, convert the numerators and denominators into single fractions, then simplify.
Start by finding the lowest common denominator in both the numerator and denominator of the complex fraction.



Add fractions with like denominators.

Simplify. Divide complex fractions by multiplying the numerator by the reciprocal of the denominator.

Solve.

To add complex fractions, convert the numerators and denominators into single fractions, then simplify.
Start by finding the lowest common denominator in both the numerator and denominator of the complex fraction.
Add fractions with like denominators.
Simplify. Divide complex fractions by multiplying the numerator by the reciprocal of the denominator.
Solve.
Compare your answer with the correct one above
Simplify,

Simplify,
To add complex fractions, convert the numerators and denominators into single fractions, then simplify.
Start by finding the lowest common denominator in both the numerator and denominator of the complex fraction.



Add fractions with like denominators.

Simplify. Divide complex fractions by multiplying the numerator by the reciprocal of the denominator.

Solve.

To add complex fractions, convert the numerators and denominators into single fractions, then simplify.
Start by finding the lowest common denominator in both the numerator and denominator of the complex fraction.
Add fractions with like denominators.
Simplify. Divide complex fractions by multiplying the numerator by the reciprocal of the denominator.
Solve.
Compare your answer with the correct one above


