Tangent - ACT Math
Card 0 of 360
For the right triangle shown below, what is the value of
 ?
?

For the right triangle shown below, what is the value of


To solve this question, you must know SOHCAHTOA. This acronym can be broken into three parts to solve for the sine, cosine, and tangent.



We can use this information to solve our identity.

Dividing by a fraction is the same as multiplying by its reciprocal.


The sine divided by cosine is the tangent of the angle.

To solve this question, you must know SOHCAHTOA. This acronym can be broken into three parts to solve for the sine, cosine, and tangent.
We can use this information to solve our identity.
Dividing by a fraction is the same as multiplying by its reciprocal.
The sine divided by cosine is the tangent of the angle.
Compare your answer with the correct one above
What is the perimeter of the following figure?

What is the perimeter of the following figure?
The question asks for you to find the perimeter of the given figure. The figure has twelve sides total, of two varying lengths. One length is given to you, 4. The other length must be solved for using either the sine or tangent functions. However, one can arrive to answer more quickly by recognizing that the drawn triangle is actually a 3-4-5 triangle, where 3, 4, and 5 corresponds to each of the sides of the triangle. This is a pythagorean triple and this ratio should be easily remembered.
Thus if 3 is the missing side, and there are eight sides of length 3 and four sides of length 4, one can arrive to the answer:

The question asks for you to find the perimeter of the given figure. The figure has twelve sides total, of two varying lengths. One length is given to you, 4. The other length must be solved for using either the sine or tangent functions. However, one can arrive to answer more quickly by recognizing that the drawn triangle is actually a 3-4-5 triangle, where 3, 4, and 5 corresponds to each of the sides of the triangle. This is a pythagorean triple and this ratio should be easily remembered.
Thus if 3 is the missing side, and there are eight sides of length 3 and four sides of length 4, one can arrive to the answer:
Compare your answer with the correct one above
A man is setting up a laser on the ground, angling it toward the very top of a flag pole. If the flag pole is  high and the laser is placed
high and the laser is placed  away from its base, what should be the angle of the laser with the ground? (Answer in degrees, rounding to the nearest hundredth.)
away from its base, what should be the angle of the laser with the ground? (Answer in degrees, rounding to the nearest hundredth.)
A man is setting up a laser on the ground, angling it toward the very top of a flag pole. If the flag pole is 

You can draw out your scenario like a triangle:

Now, you know that this means:

Using your calculator, you can utilize the inverse  function to calculate the degree measure of the angle:
function to calculate the degree measure of the angle:

This rounds to 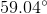 degrees.
degrees.
You can draw out your scenario like a triangle:

Now, you know that this means:
Using your calculator, you can utilize the inverse 
This rounds to 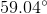
Compare your answer with the correct one above

What is the tangent of C in the given right triangle??

What is the tangent of C in the given right triangle??
Tangent = Opposite / Adjacent
Tangent = Opposite / Adjacent
Compare your answer with the correct one above
Consider a right triangle with an inner angle 
 .
.
If

and

what is  ?
?
Consider a right triangle with an inner angle 
If
and
what is 
The tangent of an angle x is defined as

Substituting the given values for cos x and sin x, we get

The tangent of an angle x is defined as

Substituting the given values for cos x and sin x, we get

Compare your answer with the correct one above

Triangle ABC shown is a right triangle. If the tangent of angle C is  , what is the length of segment BC?
, what is the length of segment BC?

Triangle ABC shown is a right triangle. If the tangent of angle C is 
Use the definition of the tangent and plug in the values given:
tangent C = Opposite / Adjacent = AB / BC = 3 / 7
Therefore, BC = 7.
Use the definition of the tangent and plug in the values given:
tangent C = Opposite / Adjacent = AB / BC = 3 / 7
Therefore, BC = 7.
Compare your answer with the correct one above
If the sine of an angle equals  , and the cosine of the same angle equals
, and the cosine of the same angle equals  , what is the tangent of the angle?
, what is the tangent of the angle?
If the sine of an angle equals 


The cosine of the angle is  and since that is a reduced fraction, we know the hypotenuse is
and since that is a reduced fraction, we know the hypotenuse is  and the adjacent side equals
and the adjacent side equals  .
.
The sine of the angle equals  , and since the hyptenuse is already
, and since the hyptenuse is already  we know that we must multiply the numerator and denominator by
we know that we must multiply the numerator and denominator by  to get the common denominator of
to get the common denominator of  . Therefore, the opposite side equals
. Therefore, the opposite side equals  .
.
Since  , the answer is
, the answer is  .
.
The cosine of the angle is 


The sine of the angle equals 




Since 

Compare your answer with the correct one above
Find the range of: 
Find the range of:
The function  is related to
is related to  . The range of the tangent function is
. The range of the tangent function is  .
.
The range of  is unaffected by the amplitude and the y-intercept. Therefore, the answer is
is unaffected by the amplitude and the y-intercept. Therefore, the answer is  .
.
The function 


The range of 

Compare your answer with the correct one above
What is the range of the trigonometric fuction defined by:
 ?
?
What is the range of the trigonometric fuction defined by:

For tangent and cotangent functions, the range is always all real numbers.
For tangent and cotangent functions, the range is always all real numbers.
Compare your answer with the correct one above
What is the range of the given trigonometric function:

What is the range of the given trigonometric function:
The range of a function is every value that the funciton's results take. For tangent and cotangent, the function spans from  and so the range is:
and so the range is:

The range of a function is every value that the funciton's results take. For tangent and cotangent, the function spans from 
Compare your answer with the correct one above
What is the tangent of the angle formed between the origin and the point  if that angle is formed with one side of the angle beginning on the
if that angle is formed with one side of the angle beginning on the  -axis and then rotating counter-clockwise to
-axis and then rotating counter-clockwise to  ? Round to the nearest hundredth.
? Round to the nearest hundredth.
What is the tangent of the angle formed between the origin and the point 


Recall that when you calculate a trigonometric function for an obtuse angle like this, you always use the  -axis as your reference point for your angle. (Hence, it is called the "reference angle.")
-axis as your reference point for your angle. (Hence, it is called the "reference angle.")
Now, it is easiest to think of this like you are drawing a little triangle in the fourth quadrant of the Cartesian plane. It would look like:

So, the tangent of an angle is:
 or, for your data,
or, for your data,  or
or  . However, since
. However, since  is in the fourth quadrant, your value must be negative. (The tangent function is negative in that quadrant.) This makes the correct answer
is in the fourth quadrant, your value must be negative. (The tangent function is negative in that quadrant.) This makes the correct answer  .
.
Recall that when you calculate a trigonometric function for an obtuse angle like this, you always use the 
Now, it is easiest to think of this like you are drawing a little triangle in the fourth quadrant of the Cartesian plane. It would look like:

So, the tangent of an angle is:





Compare your answer with the correct one above
What is the tangent of the angle formed between the origin and the point  if that angle is formed with one side of the angle beginning on the
if that angle is formed with one side of the angle beginning on the  -axis and then rotating counter-clockwise to
-axis and then rotating counter-clockwise to  ? Round to the nearest hundredth.
? Round to the nearest hundredth.
What is the tangent of the angle formed between the origin and the point 


Recall that when you calculate a trigonometric function for an obtuse angle like this, you always use the  -axis as your reference point for your angle. (Hence, it is called the "reference angle.")
-axis as your reference point for your angle. (Hence, it is called the "reference angle.")
Now, it is easiest to think of this like you are drawing a little triangle in the second quadrant of the Cartesian plane. It would look like:

So, the tangent of an angle is:
 or, for your data,
or, for your data,  .
.
This is  . Rounding, this is
. Rounding, this is  . However, since
. However, since  is in the second quadrant, your value must be negative. (The tangent function is negative in that quadrant.) Therefore, the answer is
is in the second quadrant, your value must be negative. (The tangent function is negative in that quadrant.) Therefore, the answer is  .
.
Recall that when you calculate a trigonometric function for an obtuse angle like this, you always use the 
Now, it is easiest to think of this like you are drawing a little triangle in the second quadrant of the Cartesian plane. It would look like:

So, the tangent of an angle is:


This is 



Compare your answer with the correct one above
What is the tangent of the angle formed between the origin and the point  if that angle is formed with one side of the angle beginning on the
if that angle is formed with one side of the angle beginning on the  -axis and then rotating counter-clockwise to
-axis and then rotating counter-clockwise to  ?
?
What is the tangent of the angle formed between the origin and the point 


You can begin by imagining a little triangle in the second quadrant to find your reference angle. It would look like this:

The tangent of an angle is:

For our data, this is:

Now, since this is in the second quadrant, the value is negative, given the periodic nature of the tangent function.
You can begin by imagining a little triangle in the second quadrant to find your reference angle. It would look like this:

The tangent of an angle is:
For our data, this is:
Now, since this is in the second quadrant, the value is negative, given the periodic nature of the tangent function.
Compare your answer with the correct one above
What is the tangent of the angle formed between the origin and the point  if that angle is formed with one side of the angle beginning on the
if that angle is formed with one side of the angle beginning on the  -axis and then rotating counter-clockwise to
-axis and then rotating counter-clockwise to  ? Round to the nearest hundredth.
? Round to the nearest hundredth.
What is the tangent of the angle formed between the origin and the point 


Recall that when you calculate a trigonometric function for an obtuse angle like this, you always use the  -axis as your reference point for your angle. (Hence, it is called the "reference angle.")
-axis as your reference point for your angle. (Hence, it is called the "reference angle.")
Now, it is easiest to think of this like you are drawing a little triangle in the fourth quadrant of the Cartesian plane. It would look like:

So, the tangent of an angle is:
 or, for your data,
or, for your data,  or
or  . However, since
. However, since  is in the fourth quadrant, your value must be negative. (The tangent function is negative in that quadrant.) This makes the correct answer
is in the fourth quadrant, your value must be negative. (The tangent function is negative in that quadrant.) This makes the correct answer  .
.
Recall that when you calculate a trigonometric function for an obtuse angle like this, you always use the 
Now, it is easiest to think of this like you are drawing a little triangle in the fourth quadrant of the Cartesian plane. It would look like:

So, the tangent of an angle is:





Compare your answer with the correct one above
What is the tangent of the angle formed between the origin and the point  if that angle is formed with one side of the angle beginning on the
if that angle is formed with one side of the angle beginning on the  -axis and then rotating counter-clockwise to
-axis and then rotating counter-clockwise to  ? Round to the nearest hundredth.
? Round to the nearest hundredth.
What is the tangent of the angle formed between the origin and the point 


Recall that when you calculate a trigonometric function for an obtuse angle like this, you always use the  -axis as your reference point for your angle. (Hence, it is called the "reference angle.")
-axis as your reference point for your angle. (Hence, it is called the "reference angle.")
Now, it is easiest to think of this like you are drawing a little triangle in the second quadrant of the Cartesian plane. It would look like:

So, the tangent of an angle is:
 or, for your data,
or, for your data,  .
.
This is  . Rounding, this is
. Rounding, this is  . However, since
. However, since  is in the second quadrant, your value must be negative. (The tangent function is negative in that quadrant.) Therefore, the answer is
is in the second quadrant, your value must be negative. (The tangent function is negative in that quadrant.) Therefore, the answer is  .
.
Recall that when you calculate a trigonometric function for an obtuse angle like this, you always use the 
Now, it is easiest to think of this like you are drawing a little triangle in the second quadrant of the Cartesian plane. It would look like:

So, the tangent of an angle is:


This is 



Compare your answer with the correct one above
What is the tangent of the angle formed between the origin and the point  if that angle is formed with one side of the angle beginning on the
if that angle is formed with one side of the angle beginning on the  -axis and then rotating counter-clockwise to
-axis and then rotating counter-clockwise to  ?
?
What is the tangent of the angle formed between the origin and the point 


You can begin by imagining a little triangle in the second quadrant to find your reference angle. It would look like this:

The tangent of an angle is:

For our data, this is:

Now, since this is in the second quadrant, the value is negative, given the periodic nature of the tangent function.
You can begin by imagining a little triangle in the second quadrant to find your reference angle. It would look like this:

The tangent of an angle is:
For our data, this is:
Now, since this is in the second quadrant, the value is negative, given the periodic nature of the tangent function.
Compare your answer with the correct one above

In the above triangle,  and
and  . Find
. Find  .
.

In the above triangle, 


With right triangles, we can use SOH CAH TOA to solve for unknown side lengths and angles. For this problem, we are given the opposite and adjacent sides of the triangle with relation to the angle. With this information, we can use the tangent function to find the angle.




With right triangles, we can use SOH CAH TOA to solve for unknown side lengths and angles. For this problem, we are given the opposite and adjacent sides of the triangle with relation to the angle. With this information, we can use the tangent function to find the angle.
Compare your answer with the correct one above

For the above triangle,  and
and  . Find
. Find  .
.

For the above triangle, 


With right triangles, we can use SOH CAH TOA to solve for unknown side lengths and angles. For this problem, we are given the opposite and adjacent sides of the triangle with relation to the angle. With this information, we can use the tangent function to find the angle.




With right triangles, we can use SOH CAH TOA to solve for unknown side lengths and angles. For this problem, we are given the opposite and adjacent sides of the triangle with relation to the angle. With this information, we can use the tangent function to find the angle.
Compare your answer with the correct one above

For the above triangle,  and
and  . Find
. Find  .
.

For the above triangle, 


With right triangles, we can use SOH CAH TOA to solve for unknown side lengths and angles. For this problem, we are given the opposite and adjacent sides of the triangle with relation to the angle. With this information, we can use the tangent function to find the angle.




With right triangles, we can use SOH CAH TOA to solve for unknown side lengths and angles. For this problem, we are given the opposite and adjacent sides of the triangle with relation to the angle. With this information, we can use the tangent function to find the angle.
Compare your answer with the correct one above
A laser is placed at a distance of  from the base of a building that is
from the base of a building that is  tall. What is the angle of the laser (presuming that it is at ground level) in order that it point at the top of the building?
tall. What is the angle of the laser (presuming that it is at ground level) in order that it point at the top of the building?
A laser is placed at a distance of 

You can draw your scenario using the following right triangle:

Recall that the tangent of an angle is equal to the ratio of the opposite side to the adjacent side of the triangle. You can solve for the angle by using an inverse tangent function:
 or
or  .
.
You can draw your scenario using the following right triangle:

Recall that the tangent of an angle is equal to the ratio of the opposite side to the adjacent side of the triangle. You can solve for the angle by using an inverse tangent function:


Compare your answer with the correct one above






