Function Notation - Algebra 2
Card 0 of 196
Solve for 
when 
.
Solve for
Tap to see back →
Plug 3 in for x:
Simplify:
= 
= 5
Plug 3 in for x:
Simplify:
=
= 5
What is
?
What is
Tap to see back →
To find the composition of two functions, substitute the second equation in to the first function.
Therefore,
and
Thus,
.
To find the composition of two functions, substitute the second equation in to the first function.
Therefore,
and
Thus,
Solve the function for 
. When 
What does 
equal when, 
Solve the function for
What does
Tap to see back →
Plug 16 in for 
. 
Add 9 to both sides. 
Take the square root of both sides. 
=
Final answer is 
Plug 16 in for
Add 9 to both sides.
Take the square root of both sides.
Final answer is
What is 
of the following equation?
What is
Tap to see back →
To complete an equation with a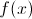 
function, plug the number inside the parentheses into the equation for 
and solve algebraically.
In this case the 
Square the 7 and multiply to get 
Add the numbers to get the answer 
.
To complete an equation with a
In this case the
Square the 7 and multiply to get
Add the numbers to get the answer
Given 
, find 
.
Given
Tap to see back →
Plug in a for x:
Next plug in (a + h) for x:
Therefore f(a+h) - f(a) = 
.
Plug in a for x:
Next plug in (a + h) for x:
Therefore f(a+h) - f(a) =
Tap to see back →
Tap to see back →
Use the function rule to find the 
for the following function:
Use the function rule to find the
Tap to see back →
Given 
, 
, plug the value for x into the given equation and evaluate:
Given
Evaluate 
if 
and 
.
Evaluate
Tap to see back →
This expression is the same as saying "take the answer of 
and plug it into 
."
First, we need to find 
. We do this by plugging 
in for 
in 
.
Now we take this answer and plug it into 
.
We can find the value of 
by replacing 
with 
.
This is our final answer.
This expression is the same as saying "take the answer of
First, we need to find
Now we take this answer and plug it into
We can find the value of
This is our final answer.
Let 
and 
. What is 
?
Let
Tap to see back →
THe notation 
is a composite function, which means we put the inside function g(x) into the outside function f(x). Essentially, we look at the original expression for f(x) and replace each x with the value of g(x).
The original expression for f(x) is 
. We will take each x and substitute in the value of g(x), which is 2x-1.
We will now distribute the -2 to the 2x - 1.
We must FOIL the 
term, because 
.
Now we collect like terms. Combine the terms with just an x.
Combine constants.
The answer is 
.
THe notation
The original expression for f(x) is
We will now distribute the -2 to the 2x - 1.
We must FOIL the
Now we collect like terms. Combine the terms with just an x.
Combine constants.
The answer is
Orange Taxi company charges passengers a $4.50 base fase, plus $0.10 per mile driven. Write a function to represent the cost of a cab ride, in terms of number of miles driven, 
.
Orange Taxi company charges passengers a $4.50 base fase, plus $0.10 per mile driven. Write a function to represent the cost of a cab ride, in terms of number of miles driven,
Tap to see back →
Total cost of the cab ride is going to equal the base fare ($4.50) plus an additional 10 cents per mile. This means the ride will always start off at $4.50. As the cab drives, the cost will increase by $0.10 each mile. This is represented as $0.10 times the number of miles. Therefore the total cost is:
Total cost of the cab ride is going to equal the base fare ($4.50) plus an additional 10 cents per mile. This means the ride will always start off at $4.50. As the cab drives, the cost will increase by $0.10 each mile. This is represented as $0.10 times the number of miles. Therefore the total cost is:
A small office building is to be built with 
long walls 
feet long and 
short walls 
feet long each. The total length of the walls is to be 
feet.
Write an equation for 
in terms of 
.
A small office building is to be built with
Write an equation for
Tap to see back →
The pre-question text provides us with all of the information required to complete this problem.
We know that the total length of the walls is to be 
ft.
We also know that we have a total of 
walls and 
walls.
With this, we can set up an equation and solve for 
.
Our equation will be with sum of all the walls set equal to the total length of the wall...
Remeber, we want 
in terms of 
, which means our equation should look like
something
Subtract 
on both sides
Divide by 
on both sides
Simplify
Answer!!!
The pre-question text provides us with all of the information required to complete this problem.
We know that the total length of the walls is to be
We also know that we have a total of
With this, we can set up an equation and solve for
Our equation will be with sum of all the walls set equal to the total length of the wall...
Remeber, we want
A cable company charges a flat $29.99 activation fee, and an additional $12.99 per month for service. How would a function of the cost be represented in terms of months of service, 
?
A cable company charges a flat $29.99 activation fee, and an additional $12.99 per month for service. How would a function of the cost be represented in terms of months of service,
Tap to see back →
The flat rate of 29.99 does not change depending on months of service. It is $29.99 no matter how long services are in use. The monthy fee is directly related to the number of months the services are in use.
The flat rate of 29.99 does not change depending on months of service. It is $29.99 no matter how long services are in use. The monthy fee is directly related to the number of months the services are in use.
What is the slope of the function 
?
What is the slope of the function
Tap to see back →
The function is written in slope-intercept form, which means:
where:
= slope
= x value
= y-intercept
Therefore, the slope is 
The function is written in slope-intercept form, which means:
where:
Therefore, the slope is
If 
, and 
, for which of the following 
value(s) will 
be an odd number?
If
Tap to see back →
First, x needs to be plugged into g(x).
Then, the resulting solution needs to be substituted into f(x).
For example,
.
Since 45 is an odd number, 7 is an x value that gives this result. Because both equations subtract an odd number to get the final result, only an odd number will result in an odd result therefore, none of the other options will give an odd result.
First, x needs to be plugged into g(x).
Then, the resulting solution needs to be substituted into f(x).
For example,
Since 45 is an odd number, 7 is an x value that gives this result. Because both equations subtract an odd number to get the final result, only an odd number will result in an odd result therefore, none of the other options will give an odd result.
Find 
for the following function:
Find
Tap to see back →
To evaluate 
, we just plug in a 
wherever we see an 
in the function, so our equation becomes
which is equal to
To evaluate
which is equal to
Find 
for the following function:
Find
Tap to see back →
To find , all we do is plug in 
wherever we see an 
in the function. We have to be sure we keep the parentheses. In this case, when we plug in 
, we get
Then, when we expand our binomial squared and distribute the 
, we get
To find
Then, when we expand our binomial squared and distribute the
Evaluate the function for 
.
Evaluate the function for
Tap to see back →
To solve for the value of the function at 
, simply plug in the value 
in place of every 
. By doing this, you will be left with the equation:
.
Another way to go about the problem is first simplifying the expression so that like terms are collected, so 
. Then to find 
, simply plug in the value 
in place of every 
. By doing this, you will be left with the equation:
.
To solve for the value of the function at
Another way to go about the problem is first simplifying the expression so that like terms are collected, so
If 
, find 
.
If
Tap to see back →
If 
then 
can be rewritten as 
. Therefore, 
. Subtracting 
from both sides of the eqauation gives 
.
If
Given 
and 
, find 
.
Given
Tap to see back →
Given f(x) and g(x), find f(g(5))
This type of problem can look intimidating depending on how it is set up. What it is asking is for us to plug g(x) into f(x) everywhere we see an x, and then to plug in 5 everywhere we still have an x. It gets a little cumbersome if approached all at once:
This looks a bit unwieldy, but this problem can be approached easily by looking at it in layers.
First, find g(5)
.
Next, plug that 15 into f(x).
So our answer is:
Given f(x) and g(x), find f(g(5))
This type of problem can look intimidating depending on how it is set up. What it is asking is for us to plug g(x) into f(x) everywhere we see an x, and then to plug in 5 everywhere we still have an x. It gets a little cumbersome if approached all at once:
This looks a bit unwieldy, but this problem can be approached easily by looking at it in layers.
First, find g(5)
Next, plug that 15 into f(x).
So our answer is: