Absolute Value - Algebra 2
Card 0 of 328
An individual's heart rate during exercise is between 
and 
of the individual's maximum heart rate. The maximum heart rate of a 
year old is 
beats per minute. Express a 
year old's target heart rate in an absolute value equation. Note: round the 
and 
endpoints to the nearest whole number.
An individual's heart rate during exercise is between
Tap to see back →
We start by finding the midpoint of the interval, which is enclosed by 60% of 204 and 80% of 204.
We find the midpoint, or average, of these endpoints by adding them and dividing by two:
142.5 is exactly 20.5 units away from both endpoints, 122 and 163. Since we are looking for the range of numbers between 122 and 163, all possible values have to be within 20.5 units of 142.5. If a number is greater than 20.5 units away from 142.5, either in the positive or negative direction, it will be outside of the \[122, 163\] interval. We can express this using absolute value in the following way:
We start by finding the midpoint of the interval, which is enclosed by 60% of 204 and 80% of 204.
We find the midpoint, or average, of these endpoints by adding them and dividing by two:
142.5 is exactly 20.5 units away from both endpoints, 122 and 163. Since we are looking for the range of numbers between 122 and 163, all possible values have to be within 20.5 units of 142.5. If a number is greater than 20.5 units away from 142.5, either in the positive or negative direction, it will be outside of the \[122, 163\] interval. We can express this using absolute value in the following way:
What is the equation of the above function?
What is the equation of the above function?
Tap to see back →
The formula of an absolute value function is 
where m is the slope, a is the horizontal shift and b is the vertical shift. The slope can be found with any two adjacent integer points, e.g. 
and 
, and plugging them into the slope formula, 
, yielding 
. The vertical and horizontal shifts are determined by where the crux of the absolute value function is. In this case, at 
, and those are your a and b, respectively.
The formula of an absolute value function is
Refer to the above figure.
Which of the following functions is graphed?
Refer to the above figure.
Which of the following functions is graphed?
Tap to see back →
Below is the graph of 
:
The given graph is the graph of 
translated by moving the graph 7 units left (that is, 
unit right) and 2 units down (that is, 
units up)
The function graphed is therefore
where 
. That is,
Below is the graph of
The given graph is the graph of
The function graphed is therefore
Refer to the above figure.
Which of the following functions is graphed?
Refer to the above figure.
Which of the following functions is graphed?
Tap to see back →
Below is the graph of :
The given graph is the graph of 
reflected in the 
-axis, then translated left 2 units (or, equivalently, right 
units. This graph is
, where 
.
The function graphed is therefore
Below is the graph of
The given graph is the graph of
The function graphed is therefore
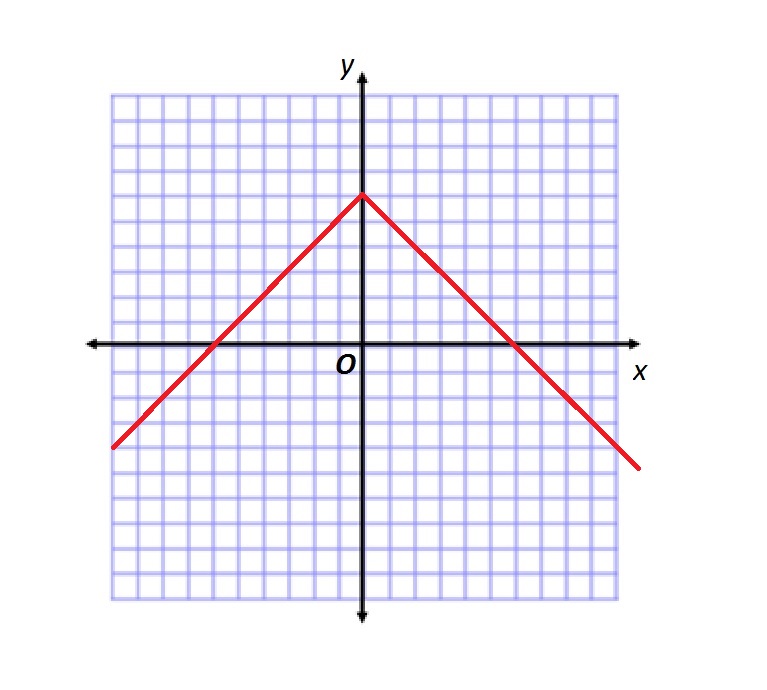
Refer to the above figure.
Which of the following functions is graphed?
Refer to the above figure.
Which of the following functions is graphed?
Tap to see back →
Below is the graph of :
The given graph is the graph of reflected in the -axis, then translated up 6 units. This graph is
, where 
.
The function graphed is therefore
Below is the graph of
The given graph is the graph of
The function graphed is therefore
Which of the following absolute value functions is represented by the following graph?
Which of the following absolute value functions is represented by the following graph?
Tap to see back →
The equation can be determined from the graph by following the rules of transformations; the base equation is:
The graph of this base equation is:
When we compare our graph to the base equation graph, we see that it has been shifted right 3 units, up 1 unit, and our graph has been stretched vertically by a factor of 2. Following the rules of transformations, the equation for our graph is written as:
The equation can be determined from the graph by following the rules of transformations; the base equation is:
The graph of this base equation is:
When we compare our graph to the base equation graph, we see that it has been shifted right 3 units, up 1 unit, and our graph has been stretched vertically by a factor of 2. Following the rules of transformations, the equation for our graph is written as:
Give the vertex of the graph of the function 
.
Give the vertex of the graph of the function
Tap to see back →
Let 
The graph of this basic absolute value function is a "V"-shaped graph with a vertex at the origin, or the point with coordinates 
. In terms of 
,
The graph of this function can be formed by shifting the graph of 
left 6 units (
) and down 7 units (
). The vertex is therefore located at 
.
Let
The graph of this basic absolute value function is a "V"-shaped graph with a vertex at the origin, or the point with coordinates
The graph of this function can be formed by shifting the graph of
Give the vertex of the graph of the function 
.
Give the vertex of the graph of the function
Tap to see back →
Let 
The graph of this basic absolute value function is a "V"-shaped graph with a vertex at the origin, or the point with coordinates 
. In terms of 
,
,
or, alternatively written,
The graph of 
is the same as that of 
, after it shifts 10 units left ( 
), it flips vertically (negative symbol), and it shifts up 10 units (the second 
). The flip does not affect the position of the vertex, but the shifts do; the vertex of the graph of 
is at 
.
Let
The graph of this basic absolute value function is a "V"-shaped graph with a vertex at the origin, or the point with coordinates
or, alternatively written,
The graph of
Solve the inequality:
Solve the inequality:
Tap to see back →
The inequality compares an absolute value function with a negative integer. Since the absolute value of any real number is greater than or equal to 0, it can never be less than a negative number. Therefore, 
can never happen. There is no solution.
The inequality compares an absolute value function with a negative integer. Since the absolute value of any real number is greater than or equal to 0, it can never be less than a negative number. Therefore,
Solve for 
:
Solve for
Tap to see back →
Solve for positive values by ignoring the absolute value. Solve for negative values by switching the inequality and adding a negative sign to 7.
Solve for positive values by ignoring the absolute value. Solve for negative values by switching the inequality and adding a negative sign to 7.
Give the solution set for the following equation:
Give the solution set for the following equation:
Tap to see back →
First, subtract 5 from both sides to get the absolute value expression alone.
Split this into two linear equations:
or
The solution set is 
First, subtract 5 from both sides to get the absolute value expression alone.
Split this into two linear equations:
or
The solution set is
In order to ride a certain roller coaster at an amusement park an individual needs to be between 
and 
pounds. Express this rule using an absolute value.
In order to ride a certain roller coaster at an amusement park an individual needs to be between
Tap to see back →
We start by finding the midpoint of the interval, which is enclosed by 90 and 210. We find the midpoint, or average, of these two endpoints by adding them and dividing by two:
150 is exactly 60 units away from both endpoints, 90 and 210. Since we are looking for the range of numbers that fall in between 90 and 210, this means that any possible value can't be more than 60 units away from 150. If a number is more than 60 units away from 150, in either the increasing or decreasing direction, it will be outside of the \[90, 210\] interval. We can express this using absolute value in the following way:
We start by finding the midpoint of the interval, which is enclosed by 90 and 210. We find the midpoint, or average, of these two endpoints by adding them and dividing by two:
150 is exactly 60 units away from both endpoints, 90 and 210. Since we are looking for the range of numbers that fall in between 90 and 210, this means that any possible value can't be more than 60 units away from 150. If a number is more than 60 units away from 150, in either the increasing or decreasing direction, it will be outside of the \[90, 210\] interval. We can express this using absolute value in the following way:
Solve for 
.
Solve for
Tap to see back →
Divide both sides by 3.
Consider both the negative and positive values for the absolute value term.
Subtract 2 from both sides to solve both scenarios for 
.
Divide both sides by 3.
Consider both the negative and positive values for the absolute value term.
Subtract 2 from both sides to solve both scenarios for
Solve for 
in the inequality below.
Solve for
Tap to see back →
The absolute value gives two problems to solve. Remember to switch the "less than" to "greater than" when comparing the negative term.
or 
Solve each inequality separately by adding 
to all sides.
or 
This can be simplified to the format 
.
The absolute value gives two problems to solve. Remember to switch the "less than" to "greater than" when comparing the negative term.
Solve each inequality separately by adding
This can be simplified to the format
Tap to see back →
Solve the inequality.
Solve the inequality.
Tap to see back →
Remove the absolute value by setting the term equal to either 
or 
. Remember to flip the inequality for the negative term!
Solve each scenario independently by subtracting 
from both sides.
Remove the absolute value by setting the term equal to either
Solve each scenario independently by subtracting
Solve for 
:
Solve for
Tap to see back →
To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.
and
This gives us:
and 
However, this question has an 
outside of the absolute value expression, in this case 
. Thus, any negative value of 
will make the right side of the equation equal to a negative number, which cannot be true for an absolute value expression. Thus, 
is an extraneous solution, as 
cannot equal a negative number.
Our final solution is then
To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.
and
This gives us:
However, this question has an
Our final solution is then
Solve for 
:
Solve for
Tap to see back →
The absolute value of any number is nonnegative, so 
must always be greater than 
. Therefore, any value of 
makes this a true statement.
The absolute value of any number is nonnegative, so
Solve the following absolute value inequality:
Solve the following absolute value inequality:
Tap to see back →
To solve this inequality, it is best to break it up into two separate inequalities to eliminate the absolute value function:
or 
.
Then, solve each one separately:
Combining these solutions gives: 
To solve this inequality, it is best to break it up into two separate inequalities to eliminate the absolute value function:
Then, solve each one separately:
Combining these solutions gives:
Which values of 
provide the full solution set for the inequality:
Which values of 
Tap to see back →
