Parabolic Functions - Algebra 2
Card 0 of 200
What is the vertex of the function  ? Is it a maximum or minimum?
? Is it a maximum or minimum?
What is the vertex of the function 
Tap to see back →
The equation of a parabola can be written in vertex form:  .
.
The point  in this format is the vertex. If
in this format is the vertex. If  is a postive number the vertex is a minimum, and if
is a postive number the vertex is a minimum, and if  is a negative number the vertex is a maximum.
is a negative number the vertex is a maximum.

In this example,  . The positive value means the vertex is a minimum.
. The positive value means the vertex is a minimum.


The equation of a parabola can be written in vertex form: 
The point 


In this example, 
What is the equation of a parabola with vertex  and
and  -intercept
-intercept  ?
?
What is the equation of a parabola with vertex 


Tap to see back →
From the vertex, we know that the equation of the parabola will take the form  for some
for some  .
.
To calculate that  , we plug in the values from the other point we are given,
, we plug in the values from the other point we are given,  , and solve for
, and solve for  :
:






Now the equation is  . This is not an answer choice, so we need to rewrite it in some way.
. This is not an answer choice, so we need to rewrite it in some way.
Expand the squared term:

Distribute the fraction through the parentheses:

Combine like terms:

From the vertex, we know that the equation of the parabola will take the form 

To calculate that 


Now the equation is 
Expand the squared term:
Distribute the fraction through the parentheses:
Combine like terms:
Find the location of the vertex for the parabola. Is it a max or min?

Find the location of the vertex for the parabola. Is it a max or min?
Tap to see back →
The polynomial is written in the form of: 
This is the standard form for a parabola.
Write the vertex formula, and substitute the known values:

The vertex is at: 
Since the coefficient of  is negative, the curve will open downward, and will have a maximum.
is negative, the curve will open downward, and will have a maximum.
The answer is: 
The polynomial is written in the form of:
This is the standard form for a parabola.
Write the vertex formula, and substitute the known values:
The vertex is at:
Since the coefficient of 
The answer is:
Which of the following graphs matches the function  ?
?
Which of the following graphs matches the function 
Tap to see back →
Start by visualizing the graph associated with the function  :
:

Terms within the parentheses associated with the squared x-variable will shift the parabola horizontally, while terms outside of the parentheses will shift the parabola vertically. In the provided equation, 2 is located outside of the parentheses and is subtracted from the terms located within the parentheses; therefore, the parabola in the graph will shift down by 2 units. A simplified graph of  looks like this:
looks like this:

Remember that there is also a term within the parentheses. Within the parentheses, 1 is subtracted from the x-variable; thus, the parabola in the graph will shift to the right by 1 unit. As a result, the following graph matches the given function  :
:
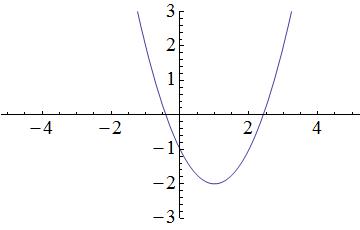
Start by visualizing the graph associated with the function 

Terms within the parentheses associated with the squared x-variable will shift the parabola horizontally, while terms outside of the parentheses will shift the parabola vertically. In the provided equation, 2 is located outside of the parentheses and is subtracted from the terms located within the parentheses; therefore, the parabola in the graph will shift down by 2 units. A simplified graph of 

Remember that there is also a term within the parentheses. Within the parentheses, 1 is subtracted from the x-variable; thus, the parabola in the graph will shift to the right by 1 unit. As a result, the following graph matches the given function 

Find the vertex form of the following quadratic equation:

Find the vertex form of the following quadratic equation:
Tap to see back →
Factor 2 as GCF from the first two terms giving us:

Now we complete the square by adding 4 to the expression inside the parenthesis and subtracting 8 ( because  ) resulting in the following equation:
) resulting in the following equation:

which is equal to

Hence the vertex is located at

Factor 2 as GCF from the first two terms giving us:
Now we complete the square by adding 4 to the expression inside the parenthesis and subtracting 8 ( because 
which is equal to
Hence the vertex is located at
A parabola is one example of a quadratic function, regardless of whether it points upwards or downwards.
The red line represents a quadratic function and will have a formula similar to  .
.
The blue line represents a linear function and will have a formula similar to  .
.
The green line represents an exponential function and will have a formula similar to  .
.
The purple line represents an absolute value function and will have a formula similar to  .
.
A parabola is one example of a quadratic function, regardless of whether it points upwards or downwards.
The red line represents a quadratic function and will have a formula similar to 
The blue line represents a linear function and will have a formula similar to 
The green line represents an exponential function and will have a formula similar to 
The purple line represents an absolute value function and will have a formula similar to 
All of the following are equations of down-facing parabolas EXCEPT:
All of the following are equations of down-facing parabolas EXCEPT:
Tap to see back →
A parabola that opens downward has the general formula
 ,
,
as the negative sign in front of the  term makes flips the parabola about the horizontal axis.
term makes flips the parabola about the horizontal axis.
By contrast, a parabola of the form  rotates about the vertical axis, not the horizontal axis.
rotates about the vertical axis, not the horizontal axis.
Therefore,  is not the equation for a parabola that opens downward.
is not the equation for a parabola that opens downward.
A parabola that opens downward has the general formula

as the negative sign in front of the 
By contrast, a parabola of the form 
Therefore, 
Consider the equation:

The vertex of this parabolic function would be located at:
Consider the equation:
The vertex of this parabolic function would be located at:
Tap to see back →
For any parabola, the general equation is
 , and the x-coordinate of its vertex is given by
, and the x-coordinate of its vertex is given by
 .
.
For the given problem, the x-coordinate is
 .
.
To find the y-coordinate, plug  into the original equation:
into the original equation:

Therefore the vertex is at  .
.
For any parabola, the general equation is


For the given problem, the x-coordinate is

To find the y-coordinate, plug 
Therefore the vertex is at 

In which direction does graph of the parabola described by the above equation open?
In which direction does graph of the parabola described by the above equation open?
Tap to see back →
Parabolas can either be in the form

for vertical parabolas or in the form

for horizontal parabolas. Since the equation that the problem gives us has a y-squared term, but not an x-squared term, we know this is a horizontal parabola. The rules for a horizontal parabola are as follows:
- If
 , then the horizontal parabola opens to the right.
, then the horizontal parabola opens to the right.
- If
 , then the horizontal parabola opens to the left.
, then the horizontal parabola opens to the left.
In this case, the coefficient in front of the y-squared term is going to be positive, once we isolate x. That makes this a horizontal parabola that opens to the right.
Parabolas can either be in the form
for vertical parabolas or in the form
for horizontal parabolas. Since the equation that the problem gives us has a y-squared term, but not an x-squared term, we know this is a horizontal parabola. The rules for a horizontal parabola are as follows:
- If
, then the horizontal parabola opens to the right.
- If
, then the horizontal parabola opens to the left.
In this case, the coefficient in front of the y-squared term is going to be positive, once we isolate x. That makes this a horizontal parabola that opens to the right.
Which of the following parabolas is downward facing?
Which of the following parabolas is downward facing?
Tap to see back →
We can determine if a parabola is upward or downward facing by looking at the coefficient of the  term. It will be downward facing if and only if this coefficient is negative. Be careful about the answer choice
term. It will be downward facing if and only if this coefficient is negative. Be careful about the answer choice  . Recall that this means that the entire value inside the parentheses will be squared. And, a negative times a negative yields a positive. Thus, this is equivalent to
. Recall that this means that the entire value inside the parentheses will be squared. And, a negative times a negative yields a positive. Thus, this is equivalent to  . Therefore, our answer has to be
. Therefore, our answer has to be  .
.
We can determine if a parabola is upward or downward facing by looking at the coefficient of the 



How many  -intercepts does the graph of the function
-intercepts does the graph of the function

have?
How many 
have?
Tap to see back →
The graph of a quadratic function  has an
has an  -intercept at any point
-intercept at any point  at which
at which  , so, first, set the quadratic expression equal to 0:
, so, first, set the quadratic expression equal to 0:

The number of  -intercepts of the graph is equal to the number of real zeroes of the above equation, which can be determined by evaluating the discriminant of the equation,
-intercepts of the graph is equal to the number of real zeroes of the above equation, which can be determined by evaluating the discriminant of the equation,  . Set
. Set  , and evaluate:
, and evaluate:

The discriminant is negative, so the equation has two solutions, neither of which are real. Consequently, the graph of the function  has no
has no  -intercepts.
-intercepts.
The graph of a quadratic function 



The number of 


The discriminant is negative, so the equation has two solutions, neither of which are real. Consequently, the graph of the function 

Write a quadratic equation having  as the vertex (vertex form of a quadratic equation).
as the vertex (vertex form of a quadratic equation).
Write a quadratic equation having 
Tap to see back →
The vertex form of a quadratic equation is given by

Where the vertex is located at 
giving us  .
.
The vertex form of a quadratic equation is given by
Where the vertex is located at
giving us 
What is the minimum possible value of the expression below?

What is the minimum possible value of the expression below?
Tap to see back →
We can determine the lowest possible value of the expression by finding the  -coordinate of the vertex of the parabola graphed from the equation
-coordinate of the vertex of the parabola graphed from the equation  . This is done by rewriting the equation in vertex form.
. This is done by rewriting the equation in vertex form.




The vertex of the parabola  is the point
is the point  .
.
The parabola is concave upward (its quadratic coefficient is positive), so  represents the minimum value of
represents the minimum value of  . This is our answer.
. This is our answer.
We can determine the lowest possible value of the expression by finding the 

The vertex of the parabola 

The parabola is concave upward (its quadratic coefficient is positive), so 

Which of the following functions represents a parabola?
Which of the following functions represents a parabola?
Tap to see back →
A parabola is a curve that can be represented by a quadratic equation. The only quadratic here is represented by the function  , while the others represent straight lines, circles, and other curves.
, while the others represent straight lines, circles, and other curves.
A parabola is a curve that can be represented by a quadratic equation. The only quadratic here is represented by the function 
Give the minimum value of the function  .
.
Give the minimum value of the function 
Tap to see back →
This is a quadratic function. The  -coordinate of the vertex of the parabola can be determined using the formula
-coordinate of the vertex of the parabola can be determined using the formula  , setting
, setting  :
:

Now evaluate the function at  :
:





This is a quadratic function. The 


Now evaluate the function at 
What are the  -intercepts of the equation?
-intercepts of the equation?

What are the 
Tap to see back →
To find the x-intercepts of the equation, we set the numerator equal to zero.




To find the x-intercepts of the equation, we set the numerator equal to zero.
Find the coordinates of the vertex of this quadratic function:

Find the coordinates of the vertex of this quadratic function:
Tap to see back →
Vertex of quadratic equation  is given by
is given by  .
.

For  ,
,

 ,
,
so the coordinate of vertex is  .
.
Vertex of quadratic equation 

For 

so the coordinate of vertex is 
What are the x-intercepts of the graph of  ?
?
What are the x-intercepts of the graph of 
Tap to see back →
Assume y=0,


 ,
, 
Assume y=0,

Find the vertex of the parabola given by the following equation:

Find the vertex of the parabola given by the following equation:
Tap to see back →
In order to find the vertex of a parabola, our first step is to find the x-coordinate of its center. If the equation of a parabola has the following form:

Then the x-coordinate of its center is given by the following formula:

For the parabola described in the problem, a=-2 and b=-12, so our center is at:

Now that we know the x-coordinate of the parabola's center, we can simply plug this value into the function to find the y-coordinate of the vertex:

So the vertex of the parabola given in the problem is at the point 
In order to find the vertex of a parabola, our first step is to find the x-coordinate of its center. If the equation of a parabola has the following form:
Then the x-coordinate of its center is given by the following formula:
For the parabola described in the problem, a=-2 and b=-12, so our center is at:
Now that we know the x-coordinate of the parabola's center, we can simply plug this value into the function to find the y-coordinate of the vertex:
So the vertex of the parabola given in the problem is at the point
Determine the maximum or minimum of  .
.
Determine the maximum or minimum of 
Tap to see back →
To find the max or min of  , use the vertex formula and substitute the appropriate coefficients.
, use the vertex formula and substitute the appropriate coefficients.

Since the leading coefficient of  is negative, the parabola opens down, which indicates that there will be a maximum.
is negative, the parabola opens down, which indicates that there will be a maximum.
The answer is: 
To find the max or min of 
Since the leading coefficient of 
The answer is:
