How to find f(x) - Algebra

Card 0 of 837

Question

There exists a function f(x) = 3_x_ + 2 for x = 2, 3, 4, 5, and 6. What is the average value of the function?

Answer

First we need to find the values of the function: f(2) = 3 * 2 + 2 = 8, f(3) = 11, f(4) = 14, f(5) = 17, and f(6) = 20. Then we can take the average of the five numbers:

average = (8 + 11 + 14 + 17 + 20) / 5 = 14

Compare your answer with the correct one above

Question

Solve the function for . When

What does equal when,

$f(x)=x^{2}-9$

Answer

Plug 16 in for .

Add 9 to both sides.

Take the square root of both sides. $\sqrt{25}$ = $\sqrt{x^{2}}$

Final answer is $\pm5$

Compare your answer with the correct one above

Question

Solve for . When .

Answer

Given the equation,

and

Plug in for to the equation,

Solve and simplify.

Compare your answer with the correct one above

Question

$f(x)=\frac{4x-2}{x+3}, x\neq-3$

Solve for , when .

Answer

$f(x)=\frac{4x-2}{x+3}, x\neq-3$

Plug in the value for .

$f(0)=\frac{4(0)-2}{(0)+3}$

Simplify

$f(0)=\frac{0-2}{3}$

Subtract

$f(0)=\frac{-2}{3}$

Compare your answer with the correct one above

Question

For the following equation, if x = 2, what is y?

Answer

On the equation, replace x with 2 and then simplify.

Compare your answer with the correct one above

Question

Find the inverse of this function.

$y=\frac{x}{x-3}$

Answer

The inverse of an equation is given by solving for the x value in terms of y. To find the inverse, take the original equation, $y=\frac{x}{x-3}$ , and solve for x.

First multiply both sides by (x – 3).

Distribute y into the parenthesis.

Subtract xy to both sides.

Factor the x.

Divide both sides by (1 – y).

$x=\frac{-3y}{1-y}$

Once you have solved for x, switch the x and y terms.

$y=\frac{-3x}{1-x}$

Though an inverse function is found by solving for x, it still must follow the "y=" convention.

Compare your answer with the correct one above

Question

Solve for when $f(x)= \frac{x^{2}+12x}{3x}$ .

Answer

Plug 3 in for x:

$f(3)=\frac{(3^{2})+123}{33}$

Simplify:

= $\frac{9+36}{9}$

= 5

Compare your answer with the correct one above

Question

What is of the following equation?

$f(x)=x^{2}+15x+35$

Answer

To complete an equation with a 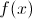function, plug the number inside the parentheses into the equation for and solve algebraically.

In this case the $f(7)=7^{2}+(15*7)+35$

Square the 7 and multiply to get

Add the numbers to get the answer .

Compare your answer with the correct one above

Question

Answer

$2\times ×36+6+2$

Compare your answer with the correct one above

Question

Answer

Compare your answer with the correct one above

Question

A function is given by $f(x)=3x^{2}+3x-4$ . Find .

Answer

Plugging in 2 wherever is present in the formula yields an answer of 14.

Compare your answer with the correct one above

Question

$\textup{If }f(p)= p^{3}-3p,;\textup{what is the value of }f(5)\textup{?}$

Answer

$\textup{Just plug in 5 every time you see }p\textup{ in the equation and solve:}$

$\left ( 5\right )^{3}-3\left ( 5\right )=125-15=110$

Compare your answer with the correct one above

Question

If $f(x) = 0.3x^{2}-9x$ , evaluate .

Answer

To solve this function, we simply need to understand that finding means that in this specific case. So, we can just substitute 10 in for .

$0.3(10)^{2}=0.3\cdot 100=30$

is equal to , so our final answer is

or .

Compare your answer with the correct one above

Question

$\textup{If }f\left(x\right )=\frac{3x^{2}-2x}{x}\textup{ , what is the value of}f\left ( 4\right )\textup{?}$

Answer

$\textup{Plug in 4 every time you see an }x\textup{ in the given equation and solve:}$

$f\left ( 4\right )=\frac{3\left ( 4\right )^{2}-2\left ( 4\right )}{4};;=\frac{48-8}{4}=10$

Compare your answer with the correct one above

Question

Each of the four tables below defines a relationship between (domain) and (range).

One of these tables does not define a function. Identified the table.

Answer

In table 3 we see an value of 3 gets tranformed into 5, 7, 9 ,and 11 which is not possible for a function. Hence the relationship between and in Table 3 does not define a function.

Compare your answer with the correct one above

Question

Each of the following 4 sets defines a relationship between and . Which of these four sets defines a one-to-one function:

A = $\left { \left ( 1,2 \right )\left ( 2,3 \right )\left ( 3,4 \right )\left ( 4,5 \right ) \right }$

B= $\left { \left ( 1,3 \right )\left ( 2,3 \right )\left ( 3,5 \right )\left ( 4,5 \right ) \right }$

C = $\left { \left ( 1,2 \right )\left ( 2,3 \right )\left ( 2,4 \right )\left ( 2,5 \right )\left ( 6,7\right )\left\right }$

D = $\left { \left ( 1,7 \right )\left ( 2,7 \right )\left ( 3,7 \right )\left ( 4,7 \right ) \right }$

Answer

Only in set A one can see that there is an unique value of for each value of and similarly each of the values maps into one and only one value. Hence set A must define a one-to-one function.

Compare your answer with the correct one above

Question

Which of the following equations does not represent a function?

$C) y = -x^{2} + 3$

$D) y^{2} = x^{2}-5$

$E) y = 2^{x}$

Answer

The correct answer is equation D. If we solve for we get

$y = \pm \sqrt{x^{2}-5}$

The fact that each value of gives us two values of $\left ( \pm )$ disqualifies it as a function.

Compare your answer with the correct one above

Question

Which of the following equations represents a one-to-one function:

$C) y = 3x^{2}-5$

$D) y^{2}= x^{2} - 5$

Answer

Only equation B maps each value of into a unique value of and in a similar way each and every value of maps into one and only one value of .

Compare your answer with the correct one above

Question

Test whether the given function is symmetric with respect to the -axis, -axis, origin.

$y = x^{3}-x^{2}$

Answer

Since $y = \left ( -x \right )^{3} -\left ( -x \right )^{2} = -x^{3}-x^{2} \neq y$

It is not symmetric with respect the -axis

$-f\left ( x \right ) = -y = -\left ( x^{3}-x^{2} \right ) = -x^{3}+x^{2}\neq f\left ( x \right )$

It is not symmetric with respect to the -axis

$-y = \left ( -x)^{3}-\left ( -x \right )^{2} = -x^{3}-x^{2}=-\left ( x^{3} \right +x^{2})$

Hence multiplying by both sides we get

$y = x^{3}+x^{2}$

Hence it is not symmetric with respect to the origin.

Compare your answer with the correct one above

Question

If , then which of the following is equivalent to ?

Answer

Plug in for .

FOIL the squared term and distribute -4:

Distribute the 2:

Combine like terms:

Compare your answer with the correct one above

Tap the card to reveal the answer