Functions, Graphs, and Limits - AP Calculus BC
Card 0 of 750

Given the above graph of  , what is
, what is  ?
?

Given the above graph of 

Tap to see back →
Examining the graph, we can observe that ") does not exist, as  is not continuous at
is not continuous at 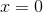 . We can see this by checking the three conditions for which a function
. We can see this by checking the three conditions for which a function  is continuous at a point
is continuous at a point 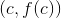 :
:
- A value
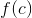 exists in the domain of
exists in the domain of 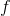
- The limit of
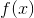 exists as
exists as 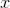 approaches
approaches 
- The limit of
 at
at  is equal to
is equal to 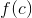
Given  , we can see that condition #1 is not satisfied because the graph has a vertical asymptote instead of only one value for
, we can see that condition #1 is not satisfied because the graph has a vertical asymptote instead of only one value for 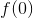 and is therefore an infinite discontinuity at
and is therefore an infinite discontinuity at 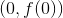 .
.
We can also see that condition #2 is not satisfied because ") approaches two different limits: from the left and
from the left and  from the right.
from the right.
Based on the above, condition #3 is also not satisfied because ") is not equal to the multiple values of 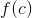 .
.
Thus, ") does not exist.
Examining the graph, we can observe that ") does not exist, as is not continuous at
. We can see this by checking the three conditions for which a function
is continuous at a point
:
- A value
exists in the domain of
- The limit of
exists as
approaches
- The limit of
at
is equal to
Given , we can see that condition #1 is not satisfied because the graph has a vertical asymptote instead of only one value for
and is therefore an infinite discontinuity at
.
We can also see that condition #2 is not satisfied because ") approaches two different limits: from the left and
from the right.
Based on the above, condition #3 is also not satisfied because ") is not equal to the multiple values of .
Thus, ") does not exist.

Given the graph of  above, what is
above, what is  ?
?

Given the graph of 

Tap to see back →
Examining the graph of the function above, we need to look at three things:
-
What is the limit of the function as it approaches zero from the left?
-
What is the limit of the function as it approaches zero from the right?
-
What is the function value at zero and is it equal to the first two statements?
If we look at the graph we see that as  approaches zero from the left the
approaches zero from the left the  values approach zero as well. This is also true if we look the values as
values approach zero as well. This is also true if we look the values as  approaches zero from the right. Lastly we look at the function value at zero which in this case is also zero.
approaches zero from the right. Lastly we look at the function value at zero which in this case is also zero.
Therefore, we can observe that  as
as  approaches
approaches  .
.
Examining the graph of the function above, we need to look at three things:
-
What is the limit of the function as it approaches zero from the left?
-
What is the limit of the function as it approaches zero from the right?
-
What is the function value at zero and is it equal to the first two statements?
If we look at the graph we see that as 


Therefore, we can observe that 



Given the graph of  above, what is
above, what is  ?
?

Given the graph of 

Tap to see back →
Examining the graph above, we need to look at three things:
-
What is the limit of the function as  approaches zero from the left?
approaches zero from the left?
-
What is the limit of the function as  approaches zero from the right?
approaches zero from the right?
-
What is the function value as  and is it the same as the result from statement one and two?
and is it the same as the result from statement one and two?
Therefore, we can determine that  does not exist, since
does not exist, since  approaches two different limits from either side :
approaches two different limits from either side :  from the left and
from the left and  from the right.
from the right.
Examining the graph above, we need to look at three things:
-
What is the limit of the function as
approaches zero from the left?
-
What is the limit of the function as
approaches zero from the right?
-
What is the function value as
and is it the same as the result from statement one and two?
Therefore, we can determine that 




Given the above graph of  , what is
, what is  ?
?
Given the above graph of 

Tap to see back →
Examining the graph, we want to find where the graph tends to as it approaches zero from the right hand side. We can see that there appears to be a vertical asymptote at zero. As the x values approach zero from the right the function values of the graph tend towards positive infinity.
Therefore, we can observe that  as
as  approaches
approaches  from the right.
from the right.
Examining the graph, we want to find where the graph tends to as it approaches zero from the right hand side. We can see that there appears to be a vertical asymptote at zero. As the x values approach zero from the right the function values of the graph tend towards positive infinity.
Therefore, we can observe that 



Tap to see back →

Tap to see back →

Tap to see back →

Tap to see back →

Tap to see back →

Tap to see back →

Tap to see back →

Tap to see back →

Tap to see back →

Tap to see back →

Tap to see back →

Tap to see back →
A cylinder of height  and radius
and radius  is expanding. The radius increases at a rate of
is expanding. The radius increases at a rate of  and its height increases at a rate of
and its height increases at a rate of  . What is the rate of growth of its surface area?
. What is the rate of growth of its surface area?
A cylinder of height 



Tap to see back →
The surface area of a cylinder is given by the formula:

To find the rate of growth over time, take the derivative of each side with respect to time:

Therefore, the rate of growth of surface area is:


The surface area of a cylinder is given by the formula:
To find the rate of growth over time, take the derivative of each side with respect to time:
Therefore, the rate of growth of surface area is:
The rate of growth of the population of Reindeer in Norway is proportional to the population. The population increased from 9876 to 10381 between 2013 and 2015. What is the expected population in 2030?
The rate of growth of the population of Reindeer in Norway is proportional to the population. The population increased from 9876 to 10381 between 2013 and 2015. What is the expected population in 2030?
Tap to see back →
We're told that the rate of growth of the population is proportional to the population itself, meaning that this problem deals with exponential growth/decay. The population can be modeled thusly:

Where  is an initial population value, and
is an initial population value, and  is the constant of proportionality.
is the constant of proportionality.
Since the population increased from 9876 to 10381 between 2013 and 2015, we can solve for this constant of proportionality:




Using this, we can calculate the expected value from 2015 to 2030:

We're told that the rate of growth of the population is proportional to the population itself, meaning that this problem deals with exponential growth/decay. The population can be modeled thusly:
Where 

Since the population increased from 9876 to 10381 between 2013 and 2015, we can solve for this constant of proportionality:
Using this, we can calculate the expected value from 2015 to 2030:
The rate of decrease due to poaching of the elephants in unprotected Sahara is proportional to the population. The population in one region decreased from 1038 to 817 between 2010 and 2015. What is the expected population in 2017?
The rate of decrease due to poaching of the elephants in unprotected Sahara is proportional to the population. The population in one region decreased from 1038 to 817 between 2010 and 2015. What is the expected population in 2017?
Tap to see back →
We're told that the rate of growth of the population is proportional to the population itself, meaning that this problem deals with exponential growth/decay. The population can be modeled thusly:

Where  is an initial population value, and
is an initial population value, and  is the constant of proportionality.
is the constant of proportionality.
Since the population decreased from 1038 to 817 between 2010 and 2015, we can solve for this constant of proportionality:




Using this, we can calculate the expected value from 2015 to 2017:

We're told that the rate of growth of the population is proportional to the population itself, meaning that this problem deals with exponential growth/decay. The population can be modeled thusly:
Where 

Since the population decreased from 1038 to 817 between 2010 and 2015, we can solve for this constant of proportionality:
Using this, we can calculate the expected value from 2015 to 2017:

Tap to see back →

























