Multiple Integration - AP Calculus BC
Card 0 of 3445
Evaluate  , where
, where  is the trapezoidal region with vertices given by
is the trapezoidal region with vertices given by  ,
,  ,
, 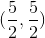 , and
, and  ,
,
using the transformation  , and
, and 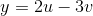 .
.
Evaluate 



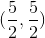

using the transformation 
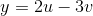
The first thing we have to do is figure out the general equations for the lines that create the trapezoid.




Now we have the general equations for out trapezoid, now we need to plug in our transformations into these equations.












So our region is a rectangle given by  ,
, 
Next we need to calculate the Jacobian.

Now we can put the integral together.

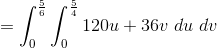

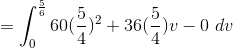



The first thing we have to do is figure out the general equations for the lines that create the trapezoid.
Now we have the general equations for out trapezoid, now we need to plug in our transformations into these equations.
So our region is a rectangle given by 
Next we need to calculate the Jacobian.
Now we can put the integral together.
Compare your answer with the correct one above
Evaluate the following integral by converting into Polar Coordinates.
 , where
, where  is the portion between the circles of radius
is the portion between the circles of radius  and
and  and lies in first quadrant.
and lies in first quadrant.
Evaluate the following integral by converting into Polar Coordinates.




We have to remember how to convert cartesian coordinates into polar coordinates.


Lets write the ranges of our variables  and
and  .
.


Now lets setup our double integral, don't forgot the extra  .
.










We have to remember how to convert cartesian coordinates into polar coordinates.
Lets write the ranges of our variables 

Now lets setup our double integral, don't forgot the extra 
Compare your answer with the correct one above
Evaluate the integral

where D is the region above the x-axis and within a circle centered at the origin of radius 2.
Evaluate the integral
where D is the region above the x-axis and within a circle centered at the origin of radius 2.
The conversions for Cartesian into polar coordinates is:

The condition that the region is above the x-axis says:

And the condition that the region is within a circle of radius two says:

With these conditions and conversions, the integral becomes:


The conversions for Cartesian into polar coordinates is:
The condition that the region is above the x-axis says:
And the condition that the region is within a circle of radius two says:
With these conditions and conversions, the integral becomes:
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above


![\begin{align*}&\theta_1=arctan(\frac{0.998}{0.063})=0.48\pi;\theta_2=arctan(\frac{-0.685}{-0.729})=1.24\pi\&\text{Now, utilizing integral rules:}\&\int[sin(ax)]=-\frac{cos(ax)}{a}\&\int_{0.48\pi}^{1.24\pi}\int_{0}^{1.49}10\cdot rcos(r^{2}))drd\theta=(5sin(r^{2}))d\theta|_{0}^{1.49}\&\int_{0.48\pi}^{1.24\pi}(3.983)d\theta=(3.983\cdot \theta)|_{0.48\pi}^{1.24\pi}=9.51\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/729257/gif.latex)


![\begin{align*}&\theta_1=arctan(\frac{0.279}{0.960})=0.09\pi;\theta_2=arctan(\frac{-0.976}{-0.218})=1.43\pi\&\text{Now, utilizing integral rules:}\&\int[re^{ar^2}]=\frac{e^{ar^2}}{2a}\&\int_{0.09\pi}^{1.43\pi}\int_{0}^{1.77}-\frac{(25\cdot re^{(-\frac{(3\cdot r^{2})}{2})})}{2})drd\theta=(\frac{(25e^{(-\frac{(3\cdot r^{2})}{2})})}{6})d\theta|_{0}^{1.77}\&\int_{0.09\pi}^{1.43\pi}(-4.129)d\theta=(-4.129\cdot \theta)|_{0.09\pi}^{1.43\pi}=-17.38\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/729655/gif.latex)


![\begin{align*}&\theta_1=arctan(\frac{0.918}{0.397})=0.37\pi;\theta_2=arctan(\frac{-0.309}{-0.951})=1.1\pi\&\text{Now, utilizing integral rules:}\&\int[rsin(ar^2)]=-\frac{cos(ar^2)}{2a}\&\int_{0.37\pi}^{1.1\pi}\int_{0}^{1.94}43\cdot rcos(\frac{r^{2}}{2}))drd\theta=(43sin(\frac{r^{2}}{2}))d\theta|_{0}^{1.94}\&\int_{0.37\pi}^{1.1\pi}(40.94)d\theta=(40.94\cdot \theta)|_{0.37\pi}^{1.1\pi}=93.88\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/729661/gif.latex)


![\begin{align*}&\theta_1=arctan(\frac{0.876}{0.482})=0.34\pi;\theta_2=arctan(\frac{-0.844}{-0.536})=1.32\pi\&\text{Now, utilizing integral rules:}\&\int[rb^{ar^2}]=\frac{e^{ar^2}}{2aln(b)}\&\int_{0.34\pi}^{1.32\pi}\int_{0}^{1.73}-41\cdot (\frac{3}{2})^{(\frac{(2\cdot r^{2})}{3})}\cdot r)drd\theta=(-\frac{(123\cdot 3^{(\frac{(2\cdot r^{2})}{3})})}{(4\cdot 2^{(\frac{(2\cdot r^{2})}{3})}ln(\frac{3}{2}))})d\theta|_{0}^{1.73}\&\int_{0.34\pi}^{1.32\pi}(-94.47)d\theta=(-94.47\cdot \theta)|_{0.34\pi}^{1.32\pi}=-290.85\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/729654/gif.latex)


![\begin{align*}&\theta_1=arctan(\frac{0.661}{0.750})=0.23\pi;\theta_2=arctan(\frac{-0.827}{-0.562})=1.31\pi\&\text{Now, utilizing integral rules:}\&\int[re^{ar^2}]=\frac{e^{ar^2}}{2a}\&\int_{0.23\pi}^{1.31\pi}\int_{0}^{1.31}(-50\cdot re^{(\frac{(2\cdot r^{2})}{3})})drd\theta=(-\frac{(75e^{(\frac{(2\cdot r^{2})}{3})})}{2})d\theta|_{0}^{1.31}\&\int_{0.23\pi}^{1.31\pi}(-80.23)d\theta=(-80.23\cdot \theta)|_{0.23\pi}^{1.31\pi}=-272.22\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/729745/gif.latex)


![\begin{align*}&\theta_1=arctan(\frac{0.482}{-0.876})=0.84\pi;\theta_2=arctan(\frac{-0.988}{-0.156})=1.45\pi\&\text{Now, utilizing integral rules:}\&\int[rsin(ar^2)]=-\frac{cos(ar^2)}{2a}\&\int_{0.84\pi}^{1.45\pi}\int_{0.5}^{1.35}(20\cdot rcos(\frac{(2\cdot r^{2})}{3}))drd\theta=(15sin(\frac{(2\cdot r^{2})}{3}))d\theta|_{0.5}^{1.35}\&\int_{0.84\pi}^{1.45\pi}(11.57)d\theta=(11.57\cdot \theta)|_{0.84\pi}^{1.45\pi}=22.18\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/729727/gif.latex)


![\begin{align*}&\theta_1=arctan(\frac{0.187}{-0.982})=0.94\pi;\theta_2=arctan(\frac{-0.397}{0.918})=1.87\pi\&\text{Now, utilizing integral rules:}\&\int[rcos(ar^2)]=\frac{sin(ar^2)}{2a}\&\int_{0.94\pi}^{1.87\pi}\int_{0.33}^{1.76}(16\cdot rsin(r^{2}))drd\theta=(-8cos(r^{2}))d\theta|_{0.33}^{1.76}\&\int_{0.94\pi}^{1.87\pi}(15.94)d\theta=(15.94\cdot \theta)|_{0.94\pi}^{1.87\pi}=46.59\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/729765/gif.latex)


![\begin{align*}&\theta_1=arctan(\frac{0.876}{0.482})=0.34\pi;\theta_2=arctan(\frac{-0.661}{0.750})=1.77\pi\&\text{Now, utilizing integral rules:}\&\int[rb^{ar^2}]=\frac{b^{ar^2}}{2aln(b)}\&\int_{0.34\pi}^{1.77\pi}\int_{0.16}^{0.97}(\frac{(49\cdot r)}{(\frac{2}{3})^{(r^{2})}})drd\theta=(-\frac{(49\cdot (\frac{3}{2})^{(r^{2})})}{(2ln(\frac{2}{3}))})d\theta|_{0.16}^{0.97}\&\int_{0.34\pi}^{1.77\pi}(27.44)d\theta=(27.44\cdot \theta)|_{0.34\pi}^{1.77\pi}=123.25\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/729736/gif.latex)


![\begin{align*}&\theta_1=arctan(\frac{0.339}{-0.941})=0.89\pi;\theta_2=arctan(\frac{-1.000}{0.031})=1.51\pi\&\text{Now, utilizing integral rules:}\&\int[re^{ar^2}]=\frac{e^{ar^2}}{2a}\&\int_{0.89\pi}^{1.51\pi}\int_{0}^{1.99}(-46\cdot re^{(2\cdot r^{2})})drd\theta=(-\frac{(23e^{(2\cdot r^{2})})}{2})d\theta|_{0}^{1.99}\&\int_{0.89\pi}^{1.51\pi}(-31644.0)d\theta=(-31644\cdot \theta)|_{0.89\pi}^{1.51\pi}=-61628.4\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/729742/gif.latex)


![\begin{align*}&\theta_1=arctan(\frac{0.094}{-0.996})=0.97\pi;\theta_2=arctan(\frac{-0.685}{0.729})=1.76\pi\&\text{Now, utilizing integral rules:}\&\int[re^{ar^2}]=\frac{e^{ar^2}}{2a}\&\int_{0.97\pi}^{1.76\pi}\int_{0}^{1.55}(45\cdot re^{(\frac{r^{2}}{2})})drd\theta=(45e^{(\frac{r^{2}}{2})})d\theta|_{0}^{1.55}\&\int_{0.97\pi}^{1.76\pi}(104.6)d\theta=(104.6\cdot \theta)|_{0.97\pi}^{1.76\pi}=259.58\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/729733/gif.latex)


![\begin{align*}&\theta_1=arctan(\frac{0.685}{-0.729})=0.76\pi;\theta_2=arctan(\frac{-0.790}{0.613})=1.71\pi\&\text{Now, utilizing integral rules:}\&\int[\frac{a}{r}]=aln(r)=ln(r^a)\&\int_{0.76\pi}^{1.71\pi}\int_{0.14}^{1.98}(\frac{24}{r^{2}}r)drd\theta=(24ln(r))d\theta|_{0.14}^{1.98}\&\int_{0.76\pi}^{1.71\pi}(63.58)d\theta=(63.58\cdot \theta)|_{0.76\pi}^{1.71\pi}=189.76\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/729730/gif.latex)


![\begin{align*}&\theta_1=arctan(\frac{0.992}{0.125})=0.46\pi;\theta_2=arctan(\frac{-0.976}{-0.218})=1.43\pi\&\text{Now, utilizing integral rules:}\&\int[\frac{a}{r}]=aln(r)=ln(r^a)\&\int_{0.46\pi}^{1.43\pi}\int_{0.43}^{1.68}(-\frac{11}{r^{2}}r)drd\theta=(-11ln(r))d\theta|_{0.43}^{1.68}\&\int_{0.46\pi}^{1.43\pi}(-14.99)d\theta=(-14.99\cdot \theta)|_{0.46\pi}^{1.43\pi}=-45.68\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/729739/gif.latex)


![\begin{align*}&\theta_1=arctan(\frac{0.707}{-0.707})=0.75\pi;\theta_2=arctan(\frac{-0.998}{0.063})=1.52\pi\&\text{Now, utilizing integral rules:}\&\int[rb^{ar^2}]=\frac{b^{ar^2}}{2aln(b)}\&\int_{0.75\pi}^{1.52\pi}\int_{0.1}^{1.76}(-\frac{(33\cdot r)}{3^{(\frac{r^{2}}{2})}})drd\theta=(\frac{33}{(3^{(\frac{r^{2}}{2})}ln(3))})d\theta|_{0.1}^{1.76}\&\int_{0.75\pi}^{1.52\pi}(-24.39)d\theta=(-24.39\cdot \theta)|_{0.75\pi}^{1.52\pi}=-59.01\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/730972/gif.latex)


![\begin{align*}&\theta_1=arctan(\frac{0.397}{-0.918})=0.87\pi;\theta_2=arctan(\frac{-0.951}{-0.309})=1.4\pi\&\text{Now, utilizing integral rules:}\&\int[rsin(ar^2)]=-\frac{cos(ar^2)}{2a}=-\frac{cos^2(\frac{a}{2}r^2)}{a}\&\int_{0.87\pi}^{1.4\pi}\int_{0.31}^{1.64}(-6\cdot rsin(2\cdot r^{2}))drd\theta=(3cos(r^{2})^{2})d\theta|_{0.31}^{1.64}\&\int_{0.87\pi}^{1.4\pi}(-0.5447)d\theta=(-0.5447\cdot \theta)|_{0.87\pi}^{1.4\pi}=-0.91\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/731004/gif.latex)


![\begin{align*}&\theta_1=arctan(\frac{0.771}{0.637})=0.28\pi;\theta_2=arctan(\frac{-0.918}{0.397})=1.63\pi\&\text{Now, utilizing integral rules:}\&\int[re^{ar^2}]=\frac{e^{ar^2}}{2a}\&\int_{0.28\pi}^{1.63\pi}\int_{0.28}^{1.32}(\frac{(3\cdot re^{(-2\cdot r^{2})})}{17})drd\theta=(-\frac{(3e^{(-2\cdot r^{2})})}{68})d\theta|_{0.28}^{1.32}\&\int_{0.28\pi}^{1.63\pi}(0.03636)d\theta=(0.03636\cdot \theta)|_{0.28\pi}^{1.63\pi}=0.15\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/731053/gif.latex)


![\begin{align*}&\theta_1=arctan(\frac{0.960}{-0.279})=0.59\pi;\theta_2=arctan(\frac{-0.454}{-0.891})=1.15\pi\&\text{Now, utilizing integral rules:}\&\int[re^{ar^2}]=\frac{e^{ar^2}}{2a}\&\int_{0.59\pi}^{1.15\pi}\int_{0.39}^{1.92}(-\frac{(45\cdot re^{(-\frac{r^{2}}{2})})}{4})drd\theta=(\frac{(45e^{(-\frac{r^{2}}{2})})}{4})d\theta|_{0.39}^{1.92}\&\int_{0.59\pi}^{1.15\pi}(-8.645)d\theta=(-8.645\cdot \theta)|_{0.59\pi}^{1.15\pi}=-15.21\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/731092/gif.latex)


![\begin{align*}&\theta_1=arctan(\frac{0.249}{-0.969})=0.92\pi;\theta_2=arctan(\frac{-1.000}{-0.031})=1.49\pi\&\text{Now, utilizing integral rules:}\&\int[re^{ar^2}]=\frac{e^{ar^2}}{2a}\&\int_{0.92\pi}^{1.49\pi}\int_{0}^{1.85}(-6\cdot re^{(-2\cdot r^{2})})drd\theta=(\frac{(3e^{(-2\cdot r^{2})})}{2})d\theta|_{0}^{1.85}\&\int_{0.92\pi}^{1.49\pi}(-1.498)d\theta=(-1.498\cdot \theta)|_{0.92\pi}^{1.49\pi}=-2.68\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/731123/gif.latex)