Polar Form - AP Calculus BC

Card 0 of 210

Rewrite in polar form:

Tap to see back →

$\left (r \cos \theta \right ) ^{2} = 3\left (r \cos \theta \right )\left (r \sin \theta \right ) + 1$

$r ^{2} \cos ^{2} \theta = 3 $r^{2}$ \cos \theta; \sin \theta \right ) + 1$

$r ^{2} \cos ^{2} \theta - 3 $r^{2}$ \cos \theta; \sin \theta \right ) = 1$

$r ^{2} \left ( \ \cos ^{2} \theta - 3 \cos \theta; \sin \theta \right ) = 1$

$r ^{2} = $\frac{1}{\cos ^{2}$ \theta - 3 \cos \theta; \sin \theta }$

$r =$\sqrt{ \frac{1}{\cos ^{2}$ \theta - 3 \cos \theta; \sin \theta }}$

Graph the equation $r=cos(\theta )$ where $0\leq \theta \leq2\pi$ .

Tap to see back →

At angle the graph as a radius of . As it approaches $\frac{\pi }{2}$ , the radius approaches .

As the graph approaches $\pi$ , the radius approaches .

Because this is a negative radius, the curve is drawn in the opposite quadrant between $\frac{3\pi }{2}$ and $2\pi$ .

Between $\pi$ and $\frac{3\pi }{2}$ , the radius approaches from and redraws the curve in the first quadrant.

Between $\frac{3\pi }{2}$ and $2\pi$ , the graph redraws the curve in the fourth quadrant as the radius approaches from .

Draw the graph of $r=cos(2\theta )$ from $0\leq \theta \leq2\pi$ .

Tap to see back →

Because this function has a period of $\pi$ , the x-intercepts of the graph happen at a reference angle of $\frac{\pi }{4}$ (angles halfway between the angles of the axes).

Between and $\frac{\pi }{4}$ the radius approaches from .

Between $\frac{\pi }{4}$ and $\frac{\pi }{2}$ , the radius approaches from and is drawn in the opposite quadrant, the third quadrant because it has a negative radius.

From $\frac{\pi }{2}$ to $\frac{3\pi }{4}$ the radius approaches from , and is drawn in the fourth quadrant, the opposite quadrant.

Between $\frac{3\pi }{4}$ and $\pi$ , the radius approaches from .

From $\pi$ and $\frac{5\pi }{4}$ , the radius approaches from .

Between $\frac{5\pi }{4}$ and $\frac{3\pi }{2}$ , the radius approaches from . Because it is a negative radius, it is drawn in the opposite quadrant, the first quadrant.

Then between $\frac{3\pi }{2}$ and $\frac{7\pi }{4}$ the radius approaches from and is draw in the second quadrant.

Finally between $\frac{7\pi }{4}$ and $2\pi$ , the radius approaches from .

What is the following coordinate in polar form?

Provide the angle in degrees.

Tap to see back →

To calculate the polar coordinate, use

$r=$\sqrt{29}$$

However, keep track of the angle here. 68 degree is the mathematical equivalent of the expression, but we know the point (-2,-5) is in the 3rd quadrant, so we have to add 180 to it to get 248.

Some calculators might already have provided you with the correct answer.

$\theta=248$ .

What is the equation in polar form?

Tap to see back →

We can convert from rectangular form to polar form by using the following identities: $y=r\sin \theta$ and $x=r\cos \theta$ . Given , then $r\sin \theta=2(r\cos \theta $)^{2}$$=2r^{2}$$\cos^{2}$ \theta$ .

$r\sin \theta=2(r\cos \theta $)^{2}$$=2r^{2}$$\cos^{2}$ \theta$ . Dividing both sides by $r\cos \theta$ ,

$\tan \theta=2r\cos \theta$

$$\frac{\tan \theta}{\cos \theta}$=2r$

$\tan \theta}{\sec \theta=2r$

$$\frac{1}{2}$\tan \theta}{\sec \theta=r$

What is the equation $y=\frac{6}{x}$$ in polar form?

Tap to see back →

We can convert from rectangular form to polar form by using the following identities: $y=r\sin \theta$ and $x=r\cos \theta$ . Given $y=\frac{6}{x}$$ , then $r\sin \theta=\frac{6}{r\cos \theta}$$ . Multiplying both sides by $r\cos \theta$ ,

$r=\sqrt$\frac{6}{\sin \theta cos \theta}$$

Convert the following function into polar form:

Tap to see back →

The following formulas were used to convert the function from polar to Cartestian coordinates:

$x=r\cos(\theta), y=r\sin(\theta), $x^2$$+y^2$$=r^2$$

Note that the last formula is a manipulation of a trignometric identity.

Simply replace these with x and y in the original function.

What is the equation in polar form?

Tap to see back →

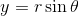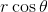We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given , then:

$r\sin\theta=-$\frac{1}{2}$(r\cos $\theta)^{2}$$

Dividing both sides by $r\cos\theta$ , we get:

$\tan \theta=-$\frac{1}{2}$r\cos\theta$

$$\frac{\tan \theta}{\cos\theta}$=-$\frac{1}{2}$r$

$\tan \theta\sec\theta=-$\frac{1}{2}$r$

$r=-2\tan \theta\sec\theta$

What is the polar form of ?

Tap to see back →

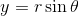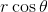We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given , then:

Dividing both sides by $r\cos\theta$ , we get:

$\tan\theta=-7r\cos\theta$

$$\frac{\tan\theta}{\cos\theta}$=-7r$

$\tan\theta\sec\theta=-7r$

$r=-$\frac{1}{7}$\tan\theta\sec\theta$

What is the polar form of ?

Tap to see back →

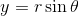We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given , then:

Dividing both sides by $r\cos\theta$ , we get:

$\tan\theta=-r\cos\theta$

$$\frac{\tan\theta}{\cos\theta}$=-r$

$\tan\theta\sec\theta=-r$

$r=-\tan\theta\sec\theta$

What is the polar form of ?

Tap to see back →

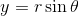We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given , then:

$r\sin\theta=-10(r\cos\theta)+5$

$r\sin\theta+10(r\cos\theta)=5$

$r(\sin\theta+10\cos\theta)=5$

$r=\frac{5}{\sin\theta+10\cos\theta}$$

What is the polar form of $y=\frac{2}{3}$x+9$ ?

Tap to see back →

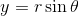We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given $y=\frac{2}{3}$x+9$ , then:

$r\sin\theta= $\frac{2}{3}$(r\cos\theta)+9$

$r\sin\theta-$\frac{2}{3}$(r\cos\theta)=9$

$r(\sin\theta-$\frac{2}{3}$\cos\theta)=9$

$r=\frac{9}{\sin\theta-\frac{2}${3}\cos\theta}$

What is the polar form of ?

Tap to see back →

We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given , then:

$r\sin\theta=3-4(r\cos\theta)$

$r\sin\theta+4(r\cos\theta)=3$

$r(\sin\theta+4\cos\theta)=3$

$r=\frac{3}{\sin\theta+4\cos\theta}$$

Find the derivative of the following function:

$r=3\theta+e^\theta$

Tap to see back →

The derivative of a polar function is given by the following:

$$\frac{dy}{dx}$=\frac{\frac{dr}{d\theta}$\sin(\theta)+r\cos(\theta)}{$\frac{dr}{d\theta}$\cos(\theta)-r\sin(\theta)}$

First, we must find $$\frac{dr}{d\theta}$=3+e^\theta$

We found the derivative using the following rules:

$$\frac{\mathrm{d}$ }{\mathrm{d} $x}e^u$$=e^u$$\frac{\mathrm{du}$ }{\mathrm{d} x}$ , $\frac{\mathrm{d}$ }{\mathrm{d} $x}x^n$$=nx^{n-1}$

Finally, we plug in the above derivative and the original function into the above formula:

$\frac{(3+e^\theta)\sin(\theta)+(3\theta+e^\theta)\cos(\theta)}{(3+e^\theta)\cos(\theta)-(3\theta+e^\theta)\sin(\theta)}$

What is the polar form of ?

Tap to see back →

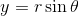We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given , then:

$r\sin\theta=2(r\cos \theta)-7$

$r\sin\theta-2(r\cos \theta)=-7$

$r(\sin\theta-2\cos \theta)=-7$

$r=-$\frac{7}{\sin\theta-2\cos \theta}$$

What is the derivative of $r=4sin\theta+2$ ?

Tap to see back →

In order to find the derivative $\frac{dy}{dx}$ of a polar equation $r=4sin\theta+2$ , we must first find the derivative of with respect to $\theta$ as follows:

$$\frac{dr}{d\theta}$=4cos\theta$

We can then swap the given values of $\frac{dr}{d\theta}$ and into the equation of the derivative of an expression into polar form:

$$\frac{dy}{dx}$=\frac{\frac{dr}{d\theta}$sin\theta+rcos\theta}{$\frac{dr}{d\theta}$cos\theta-rsin\theta}$

$\frac{dy}{dx}$=\frac{4cos\theta\sin\theta+(4sin\theta+2)cos\theta}{4cos\theta\cos\theta-(4sin\theta+2)sin\theta}$

$\frac{dy}{dx}$=\frac{4cos\theta\sin\theta+4sin\theta\cos\theta+2\cos\theta}{4cos\theta\cos\theta-4sin\theta\sin\theta-2sin\theta}$

Using the trigonometric identity , we can deduce that . Swapping this into the denominator, we get:

What is the polar form of ?

Tap to see back →

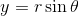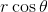We can convert from rectangular to polar form by using the following trigonometric identities: $y=r\sin\theta$ and $x=r\cos\theta$ . Given , then:

$r\sin\theta=\frac{3}$9{}(r\cos $\theta)^{2}$$

Dividing both sides by $r\cos\theta$ , we get:

$\tan \theta=\frac{3}$9{}r\cos\theta$

$$\frac{\tan \theta}{\cos\theta}$=\frac{3}{9}$r$

$\tan \theta\sec\theta=\frac{3}{9}$r$

$r=\frac{9}{3}$\tan \theta\sec\theta$

$r=3\tan \theta\sec\theta$

Convert the following cartesian coordinates into polar form:

Tap to see back →

Cartesian coordinates have x and y, represented as (x,y). Polar coordinates have $(r,\theta)$

is the hypotenuse, and $\theta$ is the angle.

$r = $$\sqrt{x^2$$+y^2$}$$

$\theta = \arctan($\frac{y}{x}$)$

Solution:

$r = $$\sqrt{x^2$$+y^2$}$$

$r = $$\sqrt{(-3)^2$$+11^2$ }$= $\sqrt{(9+121)}$$

$r = $\sqrt{130}$$

$\theta = \arctan($\frac{y}{x}$)$

$\theta = \arctan(-$\frac{11}{3}$) = -74.74$

$($\sqrt{130}$,-74.74)$

Convert the following cartesian coordinates into polar form:

Tap to see back →

Cartesian coordinates have x and y, represented as (x,y). Polar coordinates have $(r,\theta)$

is the hypotenuse, and $\theta$ is the angle.

$r = $$\sqrt{x^2$$+y^2$}$$

$\theta = \arctan($\frac{y}{x}$)$

Solution:

$r = $$\sqrt{x^2$$+y^2$}$$

$r=$\sqrt{36+196}$$

$r=$\sqrt{232}$$

$\theta=\arctan($\frac{y}{x}$)$

$\theta=\arctan($\frac{-14}{6}$)$

$\theta=-66.8$

$($\sqrt{232}$,-66.8)$

What is the derivative of $r=2+5\sin\theta$ ?

Tap to see back →

In order to find the derivative $\frac{dy}{dx}$ of a polar equation $r=2+5\sin\theta$ , we must first find the derivative of with respect to $\theta$ as follows:

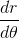$$\frac{dr}{d\theta}$=5\cos\theta$

We can then swap the given values of $\frac{dr}{d\theta}$ and into the equation of the derivative of an expression into polar form:

$$\frac{dy}{dx}$=\frac{\frac{dr}{d\theta}$\sin\theta+r\cos\theta}{$\frac{dr}{d\theta}$\cos\theta-r\sin\theta}$

$\frac{dy}{dx}$=\frac{(5\cos\theta)\sin\theta+(2+5\sin\theta)\cos\theta}{(5\cos\theta)\cos\theta-(2+5\sin\theta)\sin\theta}$

Using the trigonometric identity ![](https://lh3.googleusercontent.com/qHOZI-TYSmoUZca25iocJvaJo5lo7UOFpnRKgdd4_WnZLmZgdbZfX8GMlmTqeHc3sAuGGsKJG4zLkG9FEOQznFyOiJmHWuGk1bH-r50gZ1Gncp1EMUqk8hEF0-KplM6ZthvspP8 $"\sin^{2}$$\theta+\cos^{2}$\theta=1"), we can deduce that ![](https://lh6.googleusercontent.com/eok_ML9MG_sStGtoqEiLkZXNCirlZQ41YV4Jeclx1-Gy_BjdWZv2UfKut5ckGIphhajpaQnh4QN4Rs3SV47sUwK_3QN3O8SqSQuut3dIYiDamaNP5isQ_CBy_aLnDzOgnt8sLeQ $"\cos^{2}$$\theta=1-\sin^{2}$\theta"). Swapping this into the denominator, we get: