Substitution of Variables (by parts and simple partial fractions) - AP Calculus BC
Card 0 of 20
Tap to see back →
In order to evaluate this integral, we will need to use partial fraction decomposition.

Multiply both sides of the equation by the common denominator, which is 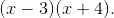


This means that  must equal 1, and
must equal 1, and 



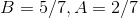
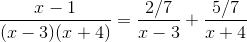
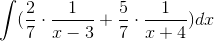



The answer is  .
.
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 
Integrate:

Integrate:
Tap to see back →
To integrate, we must first make the following substitution:

Rewriting the integral in terms of u and integrating, we get
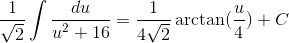
The following rule was used to integrate:

Finally, we replace u with our original x term:

To integrate, we must first make the following substitution:
Rewriting the integral in terms of u and integrating, we get
The following rule was used to integrate:
Finally, we replace u with our original x term:
Tap to see back →
In order to evaluate this integral, we will need to use partial fraction decomposition.

Multiply both sides of the equation by the common denominator, which is 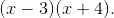


This means that  must equal 1, and
must equal 1, and 



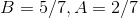
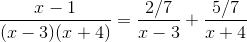
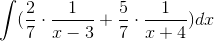



The answer is  .
.
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 
Integrate:

Integrate:
Tap to see back →
To integrate, we must first make the following substitution:

Rewriting the integral in terms of u and integrating, we get
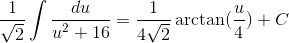
The following rule was used to integrate:

Finally, we replace u with our original x term:

To integrate, we must first make the following substitution:
Rewriting the integral in terms of u and integrating, we get
The following rule was used to integrate:
Finally, we replace u with our original x term:
Tap to see back →
In order to evaluate this integral, we will need to use partial fraction decomposition.

Multiply both sides of the equation by the common denominator, which is 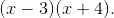


This means that  must equal 1, and
must equal 1, and 



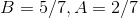
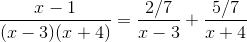
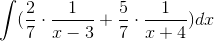



The answer is  .
.
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 
Integrate:

Integrate:
Tap to see back →
To integrate, we must first make the following substitution:

Rewriting the integral in terms of u and integrating, we get
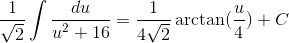
The following rule was used to integrate:

Finally, we replace u with our original x term:

To integrate, we must first make the following substitution:
Rewriting the integral in terms of u and integrating, we get
The following rule was used to integrate:
Finally, we replace u with our original x term:
Tap to see back →
In order to evaluate this integral, we will need to use partial fraction decomposition.

Multiply both sides of the equation by the common denominator, which is 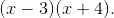


This means that  must equal 1, and
must equal 1, and 



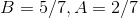
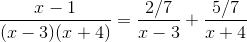
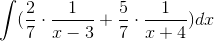



The answer is  .
.
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 
Integrate:

Integrate:
Tap to see back →
To integrate, we must first make the following substitution:

Rewriting the integral in terms of u and integrating, we get
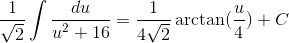
The following rule was used to integrate:

Finally, we replace u with our original x term:

To integrate, we must first make the following substitution:
Rewriting the integral in terms of u and integrating, we get
The following rule was used to integrate:
Finally, we replace u with our original x term:
Tap to see back →
In order to evaluate this integral, we will need to use partial fraction decomposition.

Multiply both sides of the equation by the common denominator, which is 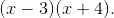


This means that  must equal 1, and
must equal 1, and 



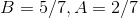
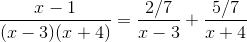
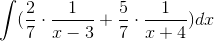



The answer is  .
.
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 
Integrate:

Integrate:
Tap to see back →
To integrate, we must first make the following substitution:

Rewriting the integral in terms of u and integrating, we get
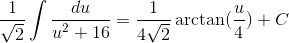
The following rule was used to integrate:

Finally, we replace u with our original x term:

To integrate, we must first make the following substitution:
Rewriting the integral in terms of u and integrating, we get
The following rule was used to integrate:
Finally, we replace u with our original x term:
Tap to see back →
In order to evaluate this integral, we will need to use partial fraction decomposition.

Multiply both sides of the equation by the common denominator, which is 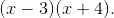


This means that  must equal 1, and
must equal 1, and 



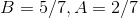
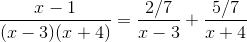



The answer is  .
.
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 
Integrate:

Integrate:
Tap to see back →
To integrate, we must first make the following substitution:

Rewriting the integral in terms of u and integrating, we get
The following rule was used to integrate:

Finally, we replace u with our original x term:

To integrate, we must first make the following substitution:
Rewriting the integral in terms of u and integrating, we get
The following rule was used to integrate:
Finally, we replace u with our original x term:
Tap to see back →
In order to evaluate this integral, we will need to use partial fraction decomposition.

Multiply both sides of the equation by the common denominator, which is 


This means that  must equal 1, and
must equal 1, and 



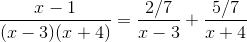
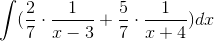



The answer is  .
.
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 
Integrate:

Integrate:
Tap to see back →
To integrate, we must first make the following substitution:

Rewriting the integral in terms of u and integrating, we get
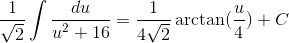
The following rule was used to integrate:

Finally, we replace u with our original x term:

To integrate, we must first make the following substitution:
Rewriting the integral in terms of u and integrating, we get
The following rule was used to integrate:
Finally, we replace u with our original x term:
Tap to see back →
In order to evaluate this integral, we will need to use partial fraction decomposition.

Multiply both sides of the equation by the common denominator, which is 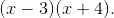


This means that  must equal 1, and
must equal 1, and 



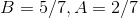
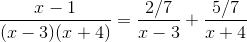
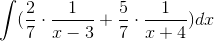



The answer is  .
.
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 
Integrate:

Integrate:
Tap to see back →
To integrate, we must first make the following substitution:

Rewriting the integral in terms of u and integrating, we get
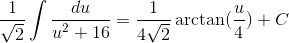
The following rule was used to integrate:

Finally, we replace u with our original x term:

To integrate, we must first make the following substitution:
Rewriting the integral in terms of u and integrating, we get
The following rule was used to integrate:
Finally, we replace u with our original x term:
Tap to see back →
In order to evaluate this integral, we will need to use partial fraction decomposition.

Multiply both sides of the equation by the common denominator, which is 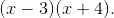


This means that  must equal 1, and
must equal 1, and 



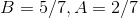
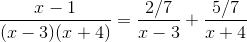
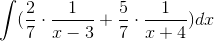



The answer is  .
.
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 
Integrate:

Integrate:
Tap to see back →
To integrate, we must first make the following substitution:

Rewriting the integral in terms of u and integrating, we get
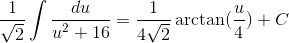
The following rule was used to integrate:

Finally, we replace u with our original x term:

To integrate, we must first make the following substitution:
Rewriting the integral in terms of u and integrating, we get
The following rule was used to integrate:
Finally, we replace u with our original x term:
Tap to see back →
In order to evaluate this integral, we will need to use partial fraction decomposition.

Multiply both sides of the equation by the common denominator, which is 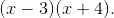


This means that  must equal 1, and
must equal 1, and 



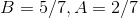
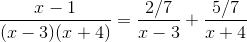
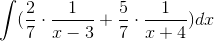



The answer is  .
.
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 
Integrate:

Integrate:
Tap to see back →
To integrate, we must first make the following substitution:

Rewriting the integral in terms of u and integrating, we get
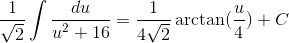
The following rule was used to integrate:

Finally, we replace u with our original x term:

To integrate, we must first make the following substitution:
Rewriting the integral in terms of u and integrating, we get
The following rule was used to integrate:
Finally, we replace u with our original x term:
