Gravity - AP Physics C: Electricity and Magnetism

Card 0 of 187

Question

A block with a mass of is traveling at $50\frac{m}{s}$ when it impacts the ground. From how many meters off the ground was the block dropped?

Round to the nearest whole number.

Answer

Set the gravitational potential energy and kinetic energy equal to each other and solve for the height.

$mgh = \frac{1}{2}mv^2$

Mass cancels.

$gh = \frac{1}{2}v^2$

Isolate the height and plug in our values.

$h = \frac{v^2}{2g} = \frac{(50\frac{m}{s})^2}{2*9.8\frac{m}{s^2}} = \frac{2500}{19.6} = 127.551m$

Rounding this gives .

Compare your answer with the correct one above

Question

A spherical asteroid has a hole drilled through the center as diagrammed below:

Refer to the diagram above. An object that is much smaller than the asteroid is released from rest at the surface of the asteroid, at point a. How do the velocity and acceleration of the object compare at point b at the surface, and point a, located at the center of the asteroid?

Answer

Because the gravitational force depends only on the mass beneath the object (which is the gravitational version of Gauss's Law for charge), the acceleration steadily decreases as the object falls, and drops to zero at the center. Nevertheless, the velocity keeps increasing as the object falls, it just does so more slowly.

Compare your answer with the correct one above

Question

An object of mass $\small m$ is dropped from a tower. The object's drag force is given by $\small F_{d}=-bv^{2}$ where $\small b$ is a positive constant. What will the objects terminal velocity be?

Answer

To find terminal velocity, set the magnitude of the drag force equal to the magnitude of the force of gravity since when these forces are equal and opposite, the object will stop accelerating:

$\small F_{d}=mg$

$\small bv^{2}=mg$

Solve for

$v=\sqrt{\frac{mg}{b}}$

Compare your answer with the correct one above

Question

A ship of mass $\small m$ and an initial velocity of $\small v_0$ is coasting to a stop. The water exerts a drag force on the ship. The drag force is proportional to the velocity:

where the negative sign indicates that the drag force acts in a direction opposite the motion. After the ship has coasted for a time equal to $\frac{2}{k}$ , how fast (in terms of $\small v_0$ ) will the ship be moving?

Answer

The ship's equation of velocity (found by solving the first-order differential equation) is $\small v=v_0e^{-kt}$

Substitute $t=\frac{2}{k}$ and solve.

Compare your answer with the correct one above

Question

A satellite is in an elliptical orbit about the Earth. If the satellite needs to enter a circular orbit at the apogee of the ellipse, in what direction will it need to accelerate?

Answer

Since the speed of the satellite at apogee is too low for a circular orbit at that orbital radius, the satellite needs to speed up to circularize the orbit.

Compare your answer with the correct one above

Question

If $v_{escape}$ is the escape velocity from the surface of a planet of mass and radius . What is the velocity necessary for an object launched from the surface of a planet of the same mass, but with a radius that is , to escape the gravitational pull of this smaller, denser planet?

Answer

Escape velocity is the velocity at which the kinetic energy of an object in motion is equal in magnitude to the gravitational potential energy. This allows us to set two equations equal to each other: the equation for kinetic energy of an object in motion and the equation for gravitational potential energy. Therefore:

$\frac{1}{2}mv^{2}=\frac{GMm}{r}$

$mv^{2}=\frac{2GMm}{r}$

$v^{2}=\frac{2GM}{r}$

$v=\sqrt{\frac{2GM}{r}}$

In this case, $v=v_{escape}$ . Substitute.

$v_{escape}=\sqrt{\frac{2GM}{r}}$

Since the radius of the new planet is or $\frac{1}{4}$ the radius of the original planet, and they have the same masses, we can equate:

$v^{}=\sqrt{\frac{2GM}{\frac{R}{4}}}=\sqrt{4}\sqrt{\frac{2GM}{R}}=2\sqrt{\frac{2GM}{R}}=2v_{escape}$

Where $v_{escape}$ is the escape velocity of the larger planet and $v^{}$ is the escape velocity of the smaller planet.

Compare your answer with the correct one above

Question

A comet is in an elliptical orbit about the Sun, as diagrammed below:

The mass of the comet is very small compared to the mass of the Sun.

In the diagram above, how does the net torque on the comet due to the Sun's gravitational force compare at the two marked points?

Answer

Since the direction of the gravitational force is directly towards the center of the Sun, it lies in the plane of the comet's orbit. Since torque is $\small r\cdot F = Fr\sin \theta$ , the torque is always zero. That is why the comet's angular momentum is conserved in orbit.

Compare your answer with the correct one above

Question

A satellite of mass is in an elliptical orbit about the Earth. It's velocity at perigee is $\small v_{p}$ and its orbital radius at perigee is $\small r_{p}$ . If the radius at apogee is $\small 2r_{p}$ , what is its velocity at apogee?

Answer

Since the gravitational force cannot exert torque on the satellite about the Earth's center, angular momentum is conserved in this orbit:

$\small L_p=L_a$

$\small mv_pr_p=mv_ar_a$

$\small v_pr_p=v_a(2r_p)$

Compare your answer with the correct one above

Question

If $v_{escape}$ is the escape velocity from the surface of a planet of mass and radius . What is the velocity necessary for an object launched from the surface of a planet of the same mass, but with a radius that is , to escape the gravitational pull of this smaller, denser planet?

Answer

Escape velocity is the velocity at which the kinetic energy of an object in motion is equal in magnitude to the gravitational potential energy. This allows us to set two equations equal to each other: the equation for kinetic energy of an object in motion and the equation for gravitational potential energy. Therefore:

$\frac{1}{2}mv^{2}=\frac{GMm}{r}$

$mv^{2}=\frac{2GMm}{r}$

$v^{2}=\frac{2GM}{r}$

$v=\sqrt{\frac{2GM}{r}}$

In this case, $v=v_{escape}$ . Substitute.

$v_{escape}=\sqrt{\frac{2GM}{r}}$

Since the radius of the new planet is or $\frac{1}{4}$ the radius of the original planet, and they have the same masses, we can equate:

$v^{}=\sqrt{\frac{2GM}{\frac{R}{4}}}=\sqrt{4}\sqrt{\frac{2GM}{R}}=2\sqrt{\frac{2GM}{R}}=2v_{escape}$

Where $v_{escape}$ is the escape velocity of the larger planet and $v^{}$ is the escape velocity of the smaller planet.

Compare your answer with the correct one above

Question

A comet is in an elliptical orbit about the Sun, as diagrammed below:

The mass of the comet is very small compared to the mass of the Sun.

In the diagram above, how does the net torque on the comet due to the Sun's gravitational force compare at the two marked points?

Answer

Since the direction of the gravitational force is directly towards the center of the Sun, it lies in the plane of the comet's orbit. Since torque is $\small r\cdot F = Fr\sin \theta$ , the torque is always zero. That is why the comet's angular momentum is conserved in orbit.

Compare your answer with the correct one above

Question

A satellite of mass is in an elliptical orbit about the Earth. It's velocity at perigee is $\small v_{p}$ and its orbital radius at perigee is $\small r_{p}$ . If the radius at apogee is $\small 2r_{p}$ , what is its velocity at apogee?

Answer

Since the gravitational force cannot exert torque on the satellite about the Earth's center, angular momentum is conserved in this orbit:

$\small L_p=L_a$

$\small mv_pr_p=mv_ar_a$

$\small v_pr_p=v_a(2r_p)$

Compare your answer with the correct one above

Question

A satellite is in an elliptical orbit about the Earth. If the satellite needs to enter a circular orbit at the apogee of the ellipse, in what direction will it need to accelerate?

Answer

Since the speed of the satellite at apogee is too low for a circular orbit at that orbital radius, the satellite needs to speed up to circularize the orbit.

Compare your answer with the correct one above

Question

The force on an object due to gravity on the moon is one-sixth of that found on Earth. What is the acceleration due to gravity on the moon?

Answer

We can use Newton's second law:

Set up equations for the force on the moon and the force on Earth:

$F_m=ma_m,\ F_E=ma_E$

Now we can use substitution:

$F_m=\frac{1}{6}F_E$

$\frac{1}{6}F_E=ma_m\rightarrow F_E=m(6a_m)$

From this, we can see that . Using the acceleration due to gravity on Earth, we can find the acceleration due to gravity on the moon.

$9.8\frac{m}{s^2}=6a_m$

$a_m=1.63\frac{m}{s^2}$

Compare your answer with the correct one above

Question

A large planet exerts a gravitational force five times stronger than that experienced on the surface of Earth. What is the weight of a 50kg object on this planet?

Answer

The weight of the object on Earth's surface is:

$F_E=ma=(50kg)(9.8\frac{m}{s^2})=490N$

The force on the new planet is five times that on Earth, so we can simply multiply:

Compare your answer with the correct one above

Question

A space woman finds herself in an unkown planet with gravity $5\frac{m}{s^2}$ . If her weight on Earth is 500N, what is her weight on the unkown planet?

$g_{Earth}=10\frac{m}{s^2}$

Answer

We know that the weight of an object is given by:

is the mass of the object and is the gravitational acceleration of whatever planet the object happens to be on.

We know the gravity on the unkown planet, so the weight of the woman is given by:

$w_{u}=mg_{u}$

We need only to find the mass of the woman to solve the problem. Since the mass of the woman is constant, we can use the information about her weight on Earth to figure out her mass.

$m=\frac{w_{e}}{g_{e}}=\frac{500N}{10\frac{m}s^2{}}=50kg$

Use this mass to solve for her weight on the new planet.

$w_{u}=mg_{u}=(50kg)(5\frac{m}{s^2})=250N$

Compare your answer with the correct one above

Question

A block with a mass of is traveling at $50\frac{m}{s}$ when it impacts the ground. From how many meters off the ground was the block dropped?

Round to the nearest whole number.

Answer

Set the gravitational potential energy and kinetic energy equal to each other and solve for the height.

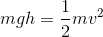
$mgh = \frac{1}{2}mv^2$

Mass cancels.

$gh = \frac{1}{2}v^2$

Isolate the height and plug in our values.

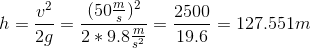
$h = \frac{v^2}{2g} = \frac{(50\frac{m}{s})^2}{2*9.8\frac{m}{s^2}} = \frac{2500}{19.6} = 127.551m$

Rounding this gives .

Compare your answer with the correct one above

Question

A spherical asteroid has a hole drilled through the center as diagrammed below:

Refer to the diagram above. An object that is much smaller than the asteroid is released from rest at the surface of the asteroid, at point a. How do the velocity and acceleration of the object compare at point b at the surface, and point a, located at the center of the asteroid?

Answer

Because the gravitational force depends only on the mass beneath the object (which is the gravitational version of Gauss's Law for charge), the acceleration steadily decreases as the object falls, and drops to zero at the center. Nevertheless, the velocity keeps increasing as the object falls, it just does so more slowly.

Compare your answer with the correct one above

Question

An object of mass $\small m$ is dropped from a tower. The object's drag force is given by $\small F_{d}=-bv^{2}$ where $\small b$ is a positive constant. What will the objects terminal velocity be?

Answer

To find terminal velocity, set the magnitude of the drag force equal to the magnitude of the force of gravity since when these forces are equal and opposite, the object will stop accelerating:

$\small F_{d}=mg$

$\small bv^{2}=mg$

Solve for

$v=\sqrt{\frac{mg}{b}}$

Compare your answer with the correct one above

Question

A ship of mass $\small m$ and an initial velocity of $\small v_0$ is coasting to a stop. The water exerts a drag force on the ship. The drag force is proportional to the velocity:

where the negative sign indicates that the drag force acts in a direction opposite the motion. After the ship has coasted for a time equal to $\frac{2}{k}$ , how fast (in terms of $\small v_0$ ) will the ship be moving?

Answer

The ship's equation of velocity (found by solving the first-order differential equation) is $\small v=v_0e^{-kt}$

Substitute $t=\frac{2}{k}$ and solve.

Compare your answer with the correct one above

Question

With what minimum velocity must a rocket be launched from the surface of the moon in order to not fall back down due to the moon's gravity?

The mass of the moon is $7.210^{22}kg$ and its radius is .

$\small G=6.6710^{-11}\frac{m^2N}{kg^2}$

Answer

Relevant equations:

$E_{total}=K+U_g$

$K = \frac{1}{2}mv^2$

$U_g=\frac{-GMm}{r}$

For the rocket to escape the moon's gravity, its minimum total energy is zero. If the total energy is zero, the rocket will have zero final velocity when it is infinitely far from the moon. If total energy is less than zero, the rocket will fall back to the moon's surface. If total energy is greater than zero, the rocket will have some final velocity when it is infinitely far away.

For the minimum energy case as the rocket leaves the surface:

$0 = K + U_g = \frac{1}{2}mv_{esc}^2 - \frac{GMm}{r}$

Rearrange energy equation to isolate the velocity term.

$v_{esc}^2 = \frac{GMm}{\frac{1}{2}mr}$

$v_{esc}=\sqrt{\frac{2GM}{r}}$

Substitute in the given values to solve for the velocity.

$v_{esc}=\sqrt{\frac{2(6.6710^{-11}\frac{m^2N}{kg^2})(7.210^{22}kg)}{(1.8*10^6m)}}=2310\frac{m}{s}\approx 2.3\frac{km}{s}$

Compare your answer with the correct one above

Tap the card to reveal the answer