Understanding Magnetic Fields and Wires - AP Physics C: Electricity and Magnetism
Card 0 of 55
Two infinitely long wires having currents  and
and  are separated by a distance
are separated by a distance  .
.

The current  is 6A into the page. The current
is 6A into the page. The current  is 9A into the page. The distance of separation is 1.5mm. The point
is 9A into the page. The distance of separation is 1.5mm. The point  lies 1.5mm away from
lies 1.5mm away from  on a line connecting the centers of the two wires.
on a line connecting the centers of the two wires.
What is the magnitude and direction of the net magnetic field at the point  ?
?

Two infinitely long wires having currents 



The current 



What is the magnitude and direction of the net magnetic field at the point 
Tap to see back →
At point  , the magnetic field due to
, the magnetic field due to  points right (via the right hand rule) with a magnitude given by:
points right (via the right hand rule) with a magnitude given by:


At point  , the magnetic field due to
, the magnetic field due to  points right (via the right hand rule) with a magnitude given by:
points right (via the right hand rule) with a magnitude given by:


The addition of these two vectors, both pointing in the same direction, results in a net magnetic field vector of magnitude  to the right.
to the right.

At point 

At point 

The addition of these two vectors, both pointing in the same direction, results in a net magnetic field vector of magnitude 

Consider a current-carrying loop with current  , radius
, radius 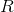 , and center
, and center  .
.
What is the direction of the magnetic field produced?

Consider a current-carrying loop with current 
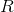

What is the direction of the magnetic field produced?
Tap to see back →
The correct answer is into the page. As the current is moving clockwise, we can use our right hand rule for magnetic fields produced by a current-carrying loop. Curl the fingers of your right hand in the direction of the current. This should result in your thumb pointing toward the screen, indicating the direction of the magnetic field.
The correct answer is into the page. As the current is moving clockwise, we can use our right hand rule for magnetic fields produced by a current-carrying loop. Curl the fingers of your right hand in the direction of the current. This should result in your thumb pointing toward the screen, indicating the direction of the magnetic field.

Consider a current-carrying loop with current  , radius
, radius  , and center
, and center  .
.
What is the magnitude of the magnetic field at point  ?
?

Consider a current-carrying loop with current 


What is the magnitude of the magnetic field at point 
Tap to see back →
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:

The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:

Consider a current-carrying loop with current  , radius
, radius  , and center
, and center  .
.
What would happen to the magnetic field at point  if the radius was halved and current was multiplied by four?
if the radius was halved and current was multiplied by four?

Consider a current-carrying loop with current 


What would happen to the magnetic field at point 
Tap to see back →
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:

Using out altered values, we can derive a ratio to determine the change in magnetic field.

The resulting field will be eight times stronger than the original.
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:
Using out altered values, we can derive a ratio to determine the change in magnetic field.
The resulting field will be eight times stronger than the original.
Consider two long, straight, current-carrying wires at distance  from each other, each with a current of magnitude
from each other, each with a current of magnitude  going in opposite directions.
going in opposite directions.
What is the magnitude of the magnetic field at a point equidistant from both wires?
Consider two long, straight, current-carrying wires at distance 

What is the magnitude of the magnetic field at a point equidistant from both wires?
Tap to see back →
Using our right hand rule for magnetic fields produced by current-carrying wires, we know that the magnetic field produced by each wire is in the same direction within the distance between the wires. Therefore, we know that the total magnetic field is simply the magnetic field of one of the wires multiplied by two.
Use the equation for magnetic field:

Multiply by two, since the magnetic field will be equal for each wire, and substitute the given variables:

Using our right hand rule for magnetic fields produced by current-carrying wires, we know that the magnetic field produced by each wire is in the same direction within the distance between the wires. Therefore, we know that the total magnetic field is simply the magnetic field of one of the wires multiplied by two.
Use the equation for magnetic field:
Multiply by two, since the magnetic field will be equal for each wire, and substitute the given variables:
Two infinitely long wires having currents  and
and  are separated by a distance
are separated by a distance  .
.

The current  is 6A into the page. The current
is 6A into the page. The current  is 9A into the page. The distance of separation is 1.5mm. The point
is 9A into the page. The distance of separation is 1.5mm. The point  lies 1.5mm away from
lies 1.5mm away from  on a line connecting the centers of the two wires.
on a line connecting the centers of the two wires.
What is the magnitude and direction of the net magnetic field at the point  ?
?

Two infinitely long wires having currents 



The current 



What is the magnitude and direction of the net magnetic field at the point 
Tap to see back →
At point  , the magnetic field due to
, the magnetic field due to  points right (via the right hand rule) with a magnitude given by:
points right (via the right hand rule) with a magnitude given by:


At point  , the magnetic field due to
, the magnetic field due to  points right (via the right hand rule) with a magnitude given by:
points right (via the right hand rule) with a magnitude given by:


The addition of these two vectors, both pointing in the same direction, results in a net magnetic field vector of magnitude  to the right.
to the right.

At point 

At point 

The addition of these two vectors, both pointing in the same direction, results in a net magnetic field vector of magnitude 

Consider a current-carrying loop with current  , radius
, radius 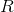 , and center
, and center  .
.
What is the direction of the magnetic field produced?

Consider a current-carrying loop with current 
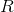

What is the direction of the magnetic field produced?
Tap to see back →
The correct answer is into the page. As the current is moving clockwise, we can use our right hand rule for magnetic fields produced by a current-carrying loop. Curl the fingers of your right hand in the direction of the current. This should result in your thumb pointing toward the screen, indicating the direction of the magnetic field.
The correct answer is into the page. As the current is moving clockwise, we can use our right hand rule for magnetic fields produced by a current-carrying loop. Curl the fingers of your right hand in the direction of the current. This should result in your thumb pointing toward the screen, indicating the direction of the magnetic field.

Consider a current-carrying loop with current  , radius
, radius  , and center
, and center  .
.
What is the magnitude of the magnetic field at point  ?
?

Consider a current-carrying loop with current 


What is the magnitude of the magnetic field at point 
Tap to see back →
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:

The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:

Consider a current-carrying loop with current  , radius
, radius  , and center
, and center  .
.
What would happen to the magnetic field at point  if the radius was halved and current was multiplied by four?
if the radius was halved and current was multiplied by four?

Consider a current-carrying loop with current 


What would happen to the magnetic field at point 
Tap to see back →
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:

Using out altered values, we can derive a ratio to determine the change in magnetic field.

The resulting field will be eight times stronger than the original.
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:
Using out altered values, we can derive a ratio to determine the change in magnetic field.
The resulting field will be eight times stronger than the original.
Consider two long, straight, current-carrying wires at distance  from each other, each with a current of magnitude
from each other, each with a current of magnitude  going in opposite directions.
going in opposite directions.
What is the magnitude of the magnetic field at a point equidistant from both wires?
Consider two long, straight, current-carrying wires at distance 

What is the magnitude of the magnetic field at a point equidistant from both wires?
Tap to see back →
Using our right hand rule for magnetic fields produced by current-carrying wires, we know that the magnetic field produced by each wire is in the same direction within the distance between the wires. Therefore, we know that the total magnetic field is simply the magnetic field of one of the wires multiplied by two.
Use the equation for magnetic field:

Multiply by two, since the magnetic field will be equal for each wire, and substitute the given variables:

Using our right hand rule for magnetic fields produced by current-carrying wires, we know that the magnetic field produced by each wire is in the same direction within the distance between the wires. Therefore, we know that the total magnetic field is simply the magnetic field of one of the wires multiplied by two.
Use the equation for magnetic field:
Multiply by two, since the magnetic field will be equal for each wire, and substitute the given variables:
Two infinitely long wires having currents  and
and  are separated by a distance
are separated by a distance  .
.

The current  is 6A into the page. The current
is 6A into the page. The current  is 9A into the page. The distance of separation is 1.5mm. The point
is 9A into the page. The distance of separation is 1.5mm. The point  lies 1.5mm away from
lies 1.5mm away from  on a line connecting the centers of the two wires.
on a line connecting the centers of the two wires.
What is the magnitude and direction of the net magnetic field at the point  ?
?

Two infinitely long wires having currents 



The current 



What is the magnitude and direction of the net magnetic field at the point 
Tap to see back →
At point  , the magnetic field due to
, the magnetic field due to  points right (via the right hand rule) with a magnitude given by:
points right (via the right hand rule) with a magnitude given by:


At point  , the magnetic field due to
, the magnetic field due to  points right (via the right hand rule) with a magnitude given by:
points right (via the right hand rule) with a magnitude given by:


The addition of these two vectors, both pointing in the same direction, results in a net magnetic field vector of magnitude  to the right.
to the right.

At point 

At point 

The addition of these two vectors, both pointing in the same direction, results in a net magnetic field vector of magnitude 

Consider a current-carrying loop with current  , radius
, radius 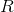 , and center
, and center  .
.
What is the direction of the magnetic field produced?

Consider a current-carrying loop with current 
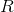

What is the direction of the magnetic field produced?
Tap to see back →
The correct answer is into the page. As the current is moving clockwise, we can use our right hand rule for magnetic fields produced by a current-carrying loop. Curl the fingers of your right hand in the direction of the current. This should result in your thumb pointing toward the screen, indicating the direction of the magnetic field.
The correct answer is into the page. As the current is moving clockwise, we can use our right hand rule for magnetic fields produced by a current-carrying loop. Curl the fingers of your right hand in the direction of the current. This should result in your thumb pointing toward the screen, indicating the direction of the magnetic field.

Consider a current-carrying loop with current  , radius
, radius  , and center
, and center  .
.
What is the magnitude of the magnetic field at point  ?
?

Consider a current-carrying loop with current 


What is the magnitude of the magnetic field at point 
Tap to see back →
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:

The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:

Consider a current-carrying loop with current  , radius
, radius  , and center
, and center  .
.
What would happen to the magnetic field at point  if the radius was halved and current was multiplied by four?
if the radius was halved and current was multiplied by four?

Consider a current-carrying loop with current 


What would happen to the magnetic field at point 
Tap to see back →
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:

Using out altered values, we can derive a ratio to determine the change in magnetic field.

The resulting field will be eight times stronger than the original.
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:
Using out altered values, we can derive a ratio to determine the change in magnetic field.
The resulting field will be eight times stronger than the original.
Consider two long, straight, current-carrying wires at distance  from each other, each with a current of magnitude
from each other, each with a current of magnitude  going in opposite directions.
going in opposite directions.
What is the magnitude of the magnetic field at a point equidistant from both wires?
Consider two long, straight, current-carrying wires at distance 

What is the magnitude of the magnetic field at a point equidistant from both wires?
Tap to see back →
Using our right hand rule for magnetic fields produced by current-carrying wires, we know that the magnetic field produced by each wire is in the same direction within the distance between the wires. Therefore, we know that the total magnetic field is simply the magnetic field of one of the wires multiplied by two.
Use the equation for magnetic field:

Multiply by two, since the magnetic field will be equal for each wire, and substitute the given variables:

Using our right hand rule for magnetic fields produced by current-carrying wires, we know that the magnetic field produced by each wire is in the same direction within the distance between the wires. Therefore, we know that the total magnetic field is simply the magnetic field of one of the wires multiplied by two.
Use the equation for magnetic field:
Multiply by two, since the magnetic field will be equal for each wire, and substitute the given variables:
Two infinitely long wires having currents  and
and  are separated by a distance
are separated by a distance  .
.

The current  is 6A into the page. The current
is 6A into the page. The current  is 9A into the page. The distance of separation is 1.5mm. The point
is 9A into the page. The distance of separation is 1.5mm. The point  lies 1.5mm away from
lies 1.5mm away from  on a line connecting the centers of the two wires.
on a line connecting the centers of the two wires.
What is the magnitude and direction of the net magnetic field at the point  ?
?

Two infinitely long wires having currents 



The current 



What is the magnitude and direction of the net magnetic field at the point 
Tap to see back →
At point  , the magnetic field due to
, the magnetic field due to  points right (via the right hand rule) with a magnitude given by:
points right (via the right hand rule) with a magnitude given by:


At point  , the magnetic field due to
, the magnetic field due to  points right (via the right hand rule) with a magnitude given by:
points right (via the right hand rule) with a magnitude given by:


The addition of these two vectors, both pointing in the same direction, results in a net magnetic field vector of magnitude  to the right.
to the right.

At point 

At point 

The addition of these two vectors, both pointing in the same direction, results in a net magnetic field vector of magnitude 

Consider a current-carrying loop with current  , radius
, radius 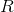 , and center
, and center  .
.
What is the direction of the magnetic field produced?

Consider a current-carrying loop with current 
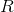

What is the direction of the magnetic field produced?
Tap to see back →
The correct answer is into the page. As the current is moving clockwise, we can use our right hand rule for magnetic fields produced by a current-carrying loop. Curl the fingers of your right hand in the direction of the current. This should result in your thumb pointing toward the screen, indicating the direction of the magnetic field.
The correct answer is into the page. As the current is moving clockwise, we can use our right hand rule for magnetic fields produced by a current-carrying loop. Curl the fingers of your right hand in the direction of the current. This should result in your thumb pointing toward the screen, indicating the direction of the magnetic field.

Consider a current-carrying loop with current  , radius
, radius  , and center
, and center  .
.
What is the magnitude of the magnetic field at point  ?
?

Consider a current-carrying loop with current 


What is the magnitude of the magnetic field at point 
Tap to see back →
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:

The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:

Consider a current-carrying loop with current  , radius
, radius  , and center
, and center  .
.
What would happen to the magnetic field at point  if the radius was halved and current was multiplied by four?
if the radius was halved and current was multiplied by four?

Consider a current-carrying loop with current 


What would happen to the magnetic field at point 
Tap to see back →
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:

Using out altered values, we can derive a ratio to determine the change in magnetic field.

The resulting field will be eight times stronger than the original.
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:
Using out altered values, we can derive a ratio to determine the change in magnetic field.
The resulting field will be eight times stronger than the original.
Consider two long, straight, current-carrying wires at distance  from each other, each with a current of magnitude
from each other, each with a current of magnitude  going in opposite directions.
going in opposite directions.
What is the magnitude of the magnetic field at a point equidistant from both wires?
Consider two long, straight, current-carrying wires at distance 

What is the magnitude of the magnetic field at a point equidistant from both wires?
Tap to see back →
Using our right hand rule for magnetic fields produced by current-carrying wires, we know that the magnetic field produced by each wire is in the same direction within the distance between the wires. Therefore, we know that the total magnetic field is simply the magnetic field of one of the wires multiplied by two.
Use the equation for magnetic field:

Multiply by two, since the magnetic field will be equal for each wire, and substitute the given variables:

Using our right hand rule for magnetic fields produced by current-carrying wires, we know that the magnetic field produced by each wire is in the same direction within the distance between the wires. Therefore, we know that the total magnetic field is simply the magnetic field of one of the wires multiplied by two.
Use the equation for magnetic field:
Multiply by two, since the magnetic field will be equal for each wire, and substitute the given variables: