How to find confidence intervals for the slope of a least-squares regression line - AP Statistics
Card 0 of 4
You estimate a regression model with  and
and  , where
, where  is the beta coefficient and
is the beta coefficient and  is the standard error. Construct 95% confidence intervals for
is the standard error. Construct 95% confidence intervals for 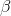 .
.
You estimate a regression model with 



Tap to see back →
To construct 95% confidence intervals for  , we simply take the coefficient and add/subtract
, we simply take the coefficient and add/subtract  . This is because
. This is because  is assumed to follow a symmetrical distribution (the normal), and 95% of the values in the sampling distribution are contained within 1.96 standard errors of
is assumed to follow a symmetrical distribution (the normal), and 95% of the values in the sampling distribution are contained within 1.96 standard errors of  .
.
To construct 95% confidence intervals for 



You estimate a regression model with  and
and  , where
, where  is the beta coefficient and
is the beta coefficient and  is the standard error. Construct 95% confidence intervals for
is the standard error. Construct 95% confidence intervals for 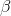 .
.
You estimate a regression model with 



Tap to see back →
To construct 95% confidence intervals for  , we simply take the coefficient and add/subtract
, we simply take the coefficient and add/subtract  . This is because
. This is because  is assumed to follow a symmetrical distribution (the normal), and 95% of the values in the sampling distribution are contained within 1.96 standard errors of
is assumed to follow a symmetrical distribution (the normal), and 95% of the values in the sampling distribution are contained within 1.96 standard errors of  .
.
To construct 95% confidence intervals for 



You estimate a regression model with  and
and  , where
, where  is the beta coefficient and
is the beta coefficient and  is the standard error. Construct 95% confidence intervals for
is the standard error. Construct 95% confidence intervals for 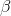 .
.
You estimate a regression model with 



Tap to see back →
To construct 95% confidence intervals for  , we simply take the coefficient and add/subtract
, we simply take the coefficient and add/subtract  . This is because
. This is because  is assumed to follow a symmetrical distribution (the normal), and 95% of the values in the sampling distribution are contained within 1.96 standard errors of
is assumed to follow a symmetrical distribution (the normal), and 95% of the values in the sampling distribution are contained within 1.96 standard errors of  .
.
To construct 95% confidence intervals for 



You estimate a regression model with  and
and  , where
, where  is the beta coefficient and
is the beta coefficient and  is the standard error. Construct 95% confidence intervals for
is the standard error. Construct 95% confidence intervals for 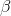 .
.
You estimate a regression model with 



Tap to see back →
To construct 95% confidence intervals for  , we simply take the coefficient and add/subtract
, we simply take the coefficient and add/subtract  . This is because
. This is because  is assumed to follow a symmetrical distribution (the normal), and 95% of the values in the sampling distribution are contained within 1.96 standard errors of
is assumed to follow a symmetrical distribution (the normal), and 95% of the values in the sampling distribution are contained within 1.96 standard errors of  .
.
To construct 95% confidence intervals for 


