How to interpret dotplots - AP Statistics
Card 0 of 12
The data points follow an overall linear trend, as opposed to being randomly distributed. Though there are a few outliers, there is a general relationship between the two variables.
A line could accurately predict the trend of the data points, suggesting there is a linear correlation. Since the y-values decrease as the x-values increase, the correlation must be negative. We can see that a line connecting the upper-most and lower-most points would have a negative slope.
An exponential relationship would be curved, rather than straight.
The data points follow an overall linear trend, as opposed to being randomly distributed. Though there are a few outliers, there is a general relationship between the two variables.
A line could accurately predict the trend of the data points, suggesting there is a linear correlation. Since the y-values decrease as the x-values increase, the correlation must be negative. We can see that a line connecting the upper-most and lower-most points would have a negative slope.
An exponential relationship would be curved, rather than straight.
A basketball coach wants to determine if a player's height can be used to predict the number of points that player scores in a season. Before using a statistical test to determine the precise relationship of the variables, the coach wants a visual of the data to see if there is likely to be a relationship. Which of the following should the coach create?
A basketball coach wants to determine if a player's height can be used to predict the number of points that player scores in a season. Before using a statistical test to determine the precise relationship of the variables, the coach wants a visual of the data to see if there is likely to be a relationship. Which of the following should the coach create?
Tap to see back →
A scatterplot is a diagram that shows the values of two variables and provides a general illustration of the relationship between them.
A scatterplot is a diagram that shows the values of two variables and provides a general illustration of the relationship between them.
Order the correlation coefficients to fit the order of the following graphs (two coefficients will not be used)
 ,
,  ,
, 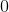 ,
,  ,
,  ,
, 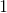

Order the correlation coefficients to fit the order of the following graphs (two coefficients will not be used)


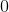



Tap to see back →
The first graph is random scatter, no correlation, the second is perfect linear, corellation  , the last two have fairly strong positive and negative corellations, the student should know that a corellation of
, the last two have fairly strong positive and negative corellations, the student should know that a corellation of  is much weaker than them
is much weaker than them
The first graph is random scatter, no correlation, the second is perfect linear, corellation 

The data points follow an overall linear trend, as opposed to being randomly distributed. Though there are a few outliers, there is a general relationship between the two variables.
A line could accurately predict the trend of the data points, suggesting there is a linear correlation. Since the y-values decrease as the x-values increase, the correlation must be negative. We can see that a line connecting the upper-most and lower-most points would have a negative slope.
An exponential relationship would be curved, rather than straight.
The data points follow an overall linear trend, as opposed to being randomly distributed. Though there are a few outliers, there is a general relationship between the two variables.
A line could accurately predict the trend of the data points, suggesting there is a linear correlation. Since the y-values decrease as the x-values increase, the correlation must be negative. We can see that a line connecting the upper-most and lower-most points would have a negative slope.
An exponential relationship would be curved, rather than straight.
A basketball coach wants to determine if a player's height can be used to predict the number of points that player scores in a season. Before using a statistical test to determine the precise relationship of the variables, the coach wants a visual of the data to see if there is likely to be a relationship. Which of the following should the coach create?
A basketball coach wants to determine if a player's height can be used to predict the number of points that player scores in a season. Before using a statistical test to determine the precise relationship of the variables, the coach wants a visual of the data to see if there is likely to be a relationship. Which of the following should the coach create?
Tap to see back →
A scatterplot is a diagram that shows the values of two variables and provides a general illustration of the relationship between them.
A scatterplot is a diagram that shows the values of two variables and provides a general illustration of the relationship between them.
Order the correlation coefficients to fit the order of the following graphs (two coefficients will not be used)
 ,
,  ,
, 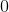 ,
,  ,
,  ,
, 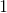

Order the correlation coefficients to fit the order of the following graphs (two coefficients will not be used)


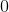



Tap to see back →
The first graph is random scatter, no correlation, the second is perfect linear, corellation  , the last two have fairly strong positive and negative corellations, the student should know that a corellation of
, the last two have fairly strong positive and negative corellations, the student should know that a corellation of  is much weaker than them
is much weaker than them
The first graph is random scatter, no correlation, the second is perfect linear, corellation 

The data points follow an overall linear trend, as opposed to being randomly distributed. Though there are a few outliers, there is a general relationship between the two variables.
A line could accurately predict the trend of the data points, suggesting there is a linear correlation. Since the y-values decrease as the x-values increase, the correlation must be negative. We can see that a line connecting the upper-most and lower-most points would have a negative slope.
An exponential relationship would be curved, rather than straight.
The data points follow an overall linear trend, as opposed to being randomly distributed. Though there are a few outliers, there is a general relationship between the two variables.
A line could accurately predict the trend of the data points, suggesting there is a linear correlation. Since the y-values decrease as the x-values increase, the correlation must be negative. We can see that a line connecting the upper-most and lower-most points would have a negative slope.
An exponential relationship would be curved, rather than straight.
A basketball coach wants to determine if a player's height can be used to predict the number of points that player scores in a season. Before using a statistical test to determine the precise relationship of the variables, the coach wants a visual of the data to see if there is likely to be a relationship. Which of the following should the coach create?
A basketball coach wants to determine if a player's height can be used to predict the number of points that player scores in a season. Before using a statistical test to determine the precise relationship of the variables, the coach wants a visual of the data to see if there is likely to be a relationship. Which of the following should the coach create?
Tap to see back →
A scatterplot is a diagram that shows the values of two variables and provides a general illustration of the relationship between them.
A scatterplot is a diagram that shows the values of two variables and provides a general illustration of the relationship between them.
Order the correlation coefficients to fit the order of the following graphs (two coefficients will not be used)
 ,
,  ,
, 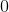 ,
,  ,
,  ,
, 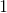

Order the correlation coefficients to fit the order of the following graphs (two coefficients will not be used)





Tap to see back →
The first graph is random scatter, no correlation, the second is perfect linear, corellation  , the last two have fairly strong positive and negative corellations, the student should know that a corellation of
, the last two have fairly strong positive and negative corellations, the student should know that a corellation of  is much weaker than them
is much weaker than them
The first graph is random scatter, no correlation, the second is perfect linear, corellation 

The data points follow an overall linear trend, as opposed to being randomly distributed. Though there are a few outliers, there is a general relationship between the two variables.
A line could accurately predict the trend of the data points, suggesting there is a linear correlation. Since the y-values decrease as the x-values increase, the correlation must be negative. We can see that a line connecting the upper-most and lower-most points would have a negative slope.
An exponential relationship would be curved, rather than straight.
The data points follow an overall linear trend, as opposed to being randomly distributed. Though there are a few outliers, there is a general relationship between the two variables.
A line could accurately predict the trend of the data points, suggesting there is a linear correlation. Since the y-values decrease as the x-values increase, the correlation must be negative. We can see that a line connecting the upper-most and lower-most points would have a negative slope.
An exponential relationship would be curved, rather than straight.
A basketball coach wants to determine if a player's height can be used to predict the number of points that player scores in a season. Before using a statistical test to determine the precise relationship of the variables, the coach wants a visual of the data to see if there is likely to be a relationship. Which of the following should the coach create?
A basketball coach wants to determine if a player's height can be used to predict the number of points that player scores in a season. Before using a statistical test to determine the precise relationship of the variables, the coach wants a visual of the data to see if there is likely to be a relationship. Which of the following should the coach create?
Tap to see back →
A scatterplot is a diagram that shows the values of two variables and provides a general illustration of the relationship between them.
A scatterplot is a diagram that shows the values of two variables and provides a general illustration of the relationship between them.
Order the correlation coefficients to fit the order of the following graphs (two coefficients will not be used)
 ,
,  ,
, 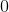 ,
,  ,
,  ,
, 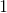

Order the correlation coefficients to fit the order of the following graphs (two coefficients will not be used)





Tap to see back →
The first graph is random scatter, no correlation, the second is perfect linear, corellation  , the last two have fairly strong positive and negative corellations, the student should know that a corellation of
, the last two have fairly strong positive and negative corellations, the student should know that a corellation of  is much weaker than them
is much weaker than them
The first graph is random scatter, no correlation, the second is perfect linear, corellation 

 and
and  variables? If so, describe the correlation.
variables? If so, describe the correlation.