Comparing Rates of Convergence - GRE Quantitative Reasoning
Card 0 of 4
For which values of p is

convergent?
For which values of p is
convergent?
We can solve this problem quite simply with the integral test. We know that if

converges, then our series converges.
We can rewrite the integral as

and then use our formula for the antiderivative of power functions to get that the integral equals
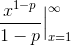 .
.
We know that this only goes to zero if 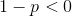 . Subtracting p from both sides, we get
. Subtracting p from both sides, we get
 .
.
We can solve this problem quite simply with the integral test. We know that if
converges, then our series converges.
We can rewrite the integral as
and then use our formula for the antiderivative of power functions to get that the integral equals
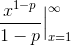
We know that this only goes to zero if 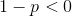

Compare your answer with the correct one above
For which values of p is

convergent?
For which values of p is
convergent?
We can solve this problem quite simply with the integral test. We know that if

converges, then our series converges.
We can rewrite the integral as

and then use our formula for the antiderivative of power functions to get that the integral equals
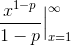 .
.
We know that this only goes to zero if 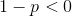 . Subtracting p from both sides, we get
. Subtracting p from both sides, we get
 .
.
We can solve this problem quite simply with the integral test. We know that if
converges, then our series converges.
We can rewrite the integral as
and then use our formula for the antiderivative of power functions to get that the integral equals
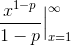
We know that this only goes to zero if 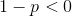

Compare your answer with the correct one above
For which values of p is

convergent?
For which values of p is
convergent?
We can solve this problem quite simply with the integral test. We know that if

converges, then our series converges.
We can rewrite the integral as

and then use our formula for the antiderivative of power functions to get that the integral equals
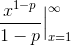 .
.
We know that this only goes to zero if 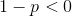 . Subtracting p from both sides, we get
. Subtracting p from both sides, we get
 .
.
We can solve this problem quite simply with the integral test. We know that if
converges, then our series converges.
We can rewrite the integral as
and then use our formula for the antiderivative of power functions to get that the integral equals
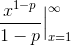
We know that this only goes to zero if 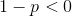

Compare your answer with the correct one above
For which values of p is

convergent?
For which values of p is
convergent?
We can solve this problem quite simply with the integral test. We know that if

converges, then our series converges.
We can rewrite the integral as

and then use our formula for the antiderivative of power functions to get that the integral equals
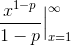 .
.
We know that this only goes to zero if 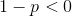 . Subtracting p from both sides, we get
. Subtracting p from both sides, we get
 .
.
We can solve this problem quite simply with the integral test. We know that if
converges, then our series converges.
We can rewrite the integral as
and then use our formula for the antiderivative of power functions to get that the integral equals
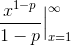
We know that this only goes to zero if 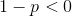

Compare your answer with the correct one above