Data Analysis - GRE Quantitative Reasoning
Card 0 of 1128
There is a bag of 28 red balls and a bag of 12 blue balls.
Quantity A: The total number of red and blue balls.
Quantity B: The number of blue balls that you can pair with one red ball.
There is a bag of 28 red balls and a bag of 12 blue balls.
Quantity A: The total number of red and blue balls.
Quantity B: The number of blue balls that you can pair with one red ball.
There are 40 total balls, and only 12 blue balls.
There are 40 total balls, and only 12 blue balls.
Compare your answer with the correct one above
Bill runs for 30 minutes at 8 mph and then runs for 15 minutes at 13mph. What was his average speed during his entire run?
Bill runs for 30 minutes at 8 mph and then runs for 15 minutes at 13mph. What was his average speed during his entire run?
Rate = distance/time.
Find the distance for each individual segment of the run (4 miles and 3.25miles). Then add total distance and divide by total time to get the average rate, while making sure the units are compatible (miles per hour not miles per minute), which means the total 45 minute run time needs to be converted to 0.75 of an hour; therefore (4miles + 3.25 miles/0.75 hour) is the final answer.
Rate = distance/time.
Find the distance for each individual segment of the run (4 miles and 3.25miles). Then add total distance and divide by total time to get the average rate, while making sure the units are compatible (miles per hour not miles per minute), which means the total 45 minute run time needs to be converted to 0.75 of an hour; therefore (4miles + 3.25 miles/0.75 hour) is the final answer.
Compare your answer with the correct one above
Three cars, A, B, and C, are in a race. A is twice as likely to win as B, and B is twice as likely to win as C. What is the probability that B or C wins?
Three cars, A, B, and C, are in a race. A is twice as likely to win as B, and B is twice as likely to win as C. What is the probability that B or C wins?
First let's find their individual probabilities of winning. Since B is twice as likely to win as C, P(B) = 2 * P(C). Since A is twice as likely to win as B, P(A) = 2 * P(B) = 2 * 2 * P(C) = 4 * P(C). We also know that the probabilities must sum to 1, so P(A) + P(B) + P(C) = 1, meaning P(C) + 2 * P(C) + 4 * P(C) = 1. Then P(C) = 1/7, so P(B) = 2 * P(C) = 2/7. Our answer is therefore P(B or C) = P(B) + P(C) = 2/7 + 1/7 = 3/7.
First let's find their individual probabilities of winning. Since B is twice as likely to win as C, P(B) = 2 * P(C). Since A is twice as likely to win as B, P(A) = 2 * P(B) = 2 * 2 * P(C) = 4 * P(C). We also know that the probabilities must sum to 1, so P(A) + P(B) + P(C) = 1, meaning P(C) + 2 * P(C) + 4 * P(C) = 1. Then P(C) = 1/7, so P(B) = 2 * P(C) = 2/7. Our answer is therefore P(B or C) = P(B) + P(C) = 2/7 + 1/7 = 3/7.
Compare your answer with the correct one above
A singing group has 10 boys and 20 girls. Half the boys and half the girls have blue eyes. What is the probability that a student chosen at random from the group is a boy OR has blue eyes?
A singing group has 10 boys and 20 girls. Half the boys and half the girls have blue eyes. What is the probability that a student chosen at random from the group is a boy OR has blue eyes?
P(boy) = 10/30 = 1/3
P(blue eyes) = 1/2
P(boy and blue eyes) = 5/30 = 1/6, because we are told that half (or 5) of the 10 boys have blue eyes
P(boy or blue eyes) = P(boy) + P(blue eyes) – P(boy and blue eyes)
= 1/3 + 1/2 – 1/6
= 2/3
P(boy) = 10/30 = 1/3
P(blue eyes) = 1/2
P(boy and blue eyes) = 5/30 = 1/6, because we are told that half (or 5) of the 10 boys have blue eyes
P(boy or blue eyes) = P(boy) + P(blue eyes) – P(boy and blue eyes)
= 1/3 + 1/2 – 1/6
= 2/3
Compare your answer with the correct one above
Four groups of college students, consisting of 15, 20, 10, and 18 people respectively, discovered their average group weights to be 162, 148, 153, and 140, respectively. What is the average weight of all the students?
Four groups of college students, consisting of 15, 20, 10, and 18 people respectively, discovered their average group weights to be 162, 148, 153, and 140, respectively. What is the average weight of all the students?
We know average = sum / number of students. Rearranging this formula gives sum = average * number of students. So to find the total average, we need to add up the four groups' sums and divide by the total number of students.
average = (15 * 162 + 20 * 148 + 10 * 153 + 18 * 140) / (15 + 20 + 10 + 18) = 150
We know average = sum / number of students. Rearranging this formula gives sum = average * number of students. So to find the total average, we need to add up the four groups' sums and divide by the total number of students.
average = (15 * 162 + 20 * 148 + 10 * 153 + 18 * 140) / (15 + 20 + 10 + 18) = 150
Compare your answer with the correct one above
Quantitative Comparison
The average weight of the 7 cats at the veterinarian's office is 8 pounds. The average weight of the 12 dogs at the vet is 16 pounds.
Quantity A: The average weight of all of the animals
Quantity B: The average weight of the cats plus the average weight of the dogs
Quantitative Comparison
The average weight of the 7 cats at the veterinarian's office is 8 pounds. The average weight of the 12 dogs at the vet is 16 pounds.
Quantity A: The average weight of all of the animals
Quantity B: The average weight of the cats plus the average weight of the dogs
Quantity B has fewer calculations so let's look at that first. We just need to add up the two averages, so Quantity B = 8 + 16 = 24.
To calculate Quantity A, we need the formula for average = total sum / total number of animals = (7 * 8 + 12 * 16) / (7 + 12) = 248/19 = 13.05.
13.05 is less than 24, so Quantity B is greater.
Quantity B has fewer calculations so let's look at that first. We just need to add up the two averages, so Quantity B = 8 + 16 = 24.
To calculate Quantity A, we need the formula for average = total sum / total number of animals = (7 * 8 + 12 * 16) / (7 + 12) = 248/19 = 13.05.
13.05 is less than 24, so Quantity B is greater.
Compare your answer with the correct one above
Alice scored an 87, 85, 90, and 73 on her first four tests of the year. If she wants to have an 87% average in the class, what must she score on her 5th test, assuming the five tests are weighted equally?
Alice scored an 87, 85, 90, and 73 on her first four tests of the year. If she wants to have an 87% average in the class, what must she score on her 5th test, assuming the five tests are weighted equally?
(87 + 85 + 90 + 73 + x) / 5 = 87
335 + x = 435
x = 100
(87 + 85 + 90 + 73 + x) / 5 = 87
335 + x = 435
x = 100
Compare your answer with the correct one above
Lucy averages 83% on her first 5 tests. What must she score on her sixth test to raise her class average to an 84, assuming all tests are weighted equally?
Lucy averages 83% on her first 5 tests. What must she score on her sixth test to raise her class average to an 84, assuming all tests are weighted equally?
For the first 5 tests, Sum / 5 = 83, so Sum = 5 * 83 = 415.
Now to solve for the last test, (415 + x) / 6 = 84. Then 415 + x = 504, and x = 89.
For the first 5 tests, Sum / 5 = 83, so Sum = 5 * 83 = 415.
Now to solve for the last test, (415 + x) / 6 = 84. Then 415 + x = 504, and x = 89.
Compare your answer with the correct one above
There exists a function f(x) = 3_x_ + 2 for x = 2, 3, 4, 5, and 6. What is the average value of the function?
There exists a function f(x) = 3_x_ + 2 for x = 2, 3, 4, 5, and 6. What is the average value of the function?
First we need to find the values of the function: f(2) = 3 * 2 + 2 = 8, f(3) = 11, f(4) = 14, f(5) = 17, and f(6) = 20. Then we can take the average of the five numbers:
average = (8 + 11 + 14 + 17 + 20) / 5 = 14
First we need to find the values of the function: f(2) = 3 * 2 + 2 = 8, f(3) = 11, f(4) = 14, f(5) = 17, and f(6) = 20. Then we can take the average of the five numbers:
average = (8 + 11 + 14 + 17 + 20) / 5 = 14
Compare your answer with the correct one above
What is the arithmetic mean (average) of the following set of numbers:
34, 26, 18, 12, 40
What is the arithmetic mean (average) of the following set of numbers:
34, 26, 18, 12, 40
If in a set of numbers, the numbers are: x, x-b, x + b, y - a, y + a, the average is automatically x.
To find the average, add up the sum of all the numbers and divide by the number of items present.
If in a set of numbers, the numbers are: x, x-b, x + b, y - a, y + a, the average is automatically x.
To find the average, add up the sum of all the numbers and divide by the number of items present.
Compare your answer with the correct one above
What is the average (arithmetic mean) of all multiples of five from 5 to 45 inclusive?
What is the average (arithmetic mean) of all multiples of five from 5 to 45 inclusive?
All multiples of 5 must first be added.
5 + 10 + 15 + 20 + 25 + 30 + 35 + 40 + 45 = 225
Because we added 9 terms, the product must be divided by 9.
225 / 9 = 25.
25 is the average.
All multiples of 5 must first be added.
5 + 10 + 15 + 20 + 25 + 30 + 35 + 40 + 45 = 225
Because we added 9 terms, the product must be divided by 9.
225 / 9 = 25.
25 is the average.
Compare your answer with the correct one above
Find the mode of the following set of numbers:
4,6,12,9,12,90,12,18,12,12,12,4,4,4,9,7,76
Find the mode of the following set of numbers:
4,6,12,9,12,90,12,18,12,12,12,4,4,4,9,7,76
Mode is the item that appears most often.
Mode is the item that appears most often.
Compare your answer with the correct one above
Find the mode:

Find the mode:
The mode is the number that appears most frequently in a given set.
The mode is the number that appears most frequently in a given set.
Compare your answer with the correct one above
A given company has 1500 employees. Of those employees, 800 are computer science majors. 25% of those computer science majors are also mathematics majors. That group of computer science/math dual majors makes up one third of the total mathematics majors. How many employees have majors other than computer science and mathematics?
A given company has 1500 employees. Of those employees, 800 are computer science majors. 25% of those computer science majors are also mathematics majors. That group of computer science/math dual majors makes up one third of the total mathematics majors. How many employees have majors other than computer science and mathematics?
Refer to the following Venn Diagram:
If 25% of the 800 CS students are also mathematics students, the number of students sharing these majors is 800 * 0.25 or 200 students. Furthermore, if this represents one third of the total of math students, we then know:
Math students * 1/3 = 200 or (1/3)M = 200
Solving for M we get 600. This means that the number of students that are ONLY math students is 400.
Looking at our diagram above, we must be careful not to "double add" the intersection. The easiest way to do this is to take the intersection and add to it the number of CS-only and math-only students: 600 + 200 + 400 = 1200. This number represents the total number of students that have either a math or CS major (that is, the number of students in the union of the two sets). This leaves 1500 – 1200 or 300 students.
Refer to the following Venn Diagram:
If 25% of the 800 CS students are also mathematics students, the number of students sharing these majors is 800 * 0.25 or 200 students. Furthermore, if this represents one third of the total of math students, we then know:
Math students * 1/3 = 200 or (1/3)M = 200
Solving for M we get 600. This means that the number of students that are ONLY math students is 400.
Looking at our diagram above, we must be careful not to "double add" the intersection. The easiest way to do this is to take the intersection and add to it the number of CS-only and math-only students: 600 + 200 + 400 = 1200. This number represents the total number of students that have either a math or CS major (that is, the number of students in the union of the two sets). This leaves 1500 – 1200 or 300 students.
Compare your answer with the correct one above
In a class, there are 15 students who like chocolate. 13 students like vanilla. 10 students like neither. If there are 35 people in the class, how many students like chocolate and vanilla?
In a class, there are 15 students who like chocolate. 13 students like vanilla. 10 students like neither. If there are 35 people in the class, how many students like chocolate and vanilla?
In order to find the intersection of chocolate and vanilla, it is easiest to make a Venn Diagram. The outside of the Venn Diagram is 10, and the total of the entire diagram must equal 35. Therefore the two circles of the Venn Diagram including just chocolate, just vanilla and the intersection must equal 25, with the just chocolate plus intersection side equalling 15 and the just vanilla plus intersection side equalling 13.
We know:
(A U B) = A + B – (A ∩ B)
We have found that (A U B) = 25 and we are trying to find (A ∩ B). Plug in A and B
25 = 15 + 13 – (A ∩ B) = 28 – (A ∩ B)
or – (A ∩ B) = –3
(A ∩ B) = 3
In order to find the intersection of chocolate and vanilla, it is easiest to make a Venn Diagram. The outside of the Venn Diagram is 10, and the total of the entire diagram must equal 35. Therefore the two circles of the Venn Diagram including just chocolate, just vanilla and the intersection must equal 25, with the just chocolate plus intersection side equalling 15 and the just vanilla plus intersection side equalling 13.
We know:
(A U B) = A + B – (A ∩ B)
We have found that (A U B) = 25 and we are trying to find (A ∩ B). Plug in A and B
25 = 15 + 13 – (A ∩ B) = 28 – (A ∩ B)
or – (A ∩ B) = –3
(A ∩ B) = 3
Compare your answer with the correct one above
In a population of cats, 10% are tabby colored, 5% are pregnant, and 3% are both tabby and pregnant. What is the probability that a cat is tabby but not pregnant?
In a population of cats, 10% are tabby colored, 5% are pregnant, and 3% are both tabby and pregnant. What is the probability that a cat is tabby but not pregnant?
Probability (tabby but not pregnant)
= Prob (tabby) – Prob (tabby and pregnant)
= 10% - 3%
= 7%
Probability (tabby but not pregnant)
= Prob (tabby) – Prob (tabby and pregnant)
= 10% - 3%
= 7%
Compare your answer with the correct one above
At an overpriced department store there are  customers. If
customers. If  have purchased shirts,
have purchased shirts,  have purchased pants, and
have purchased pants, and  have purchased neither, how many purchased both shirts and pants?
have purchased neither, how many purchased both shirts and pants?
At an overpriced department store there are 



A way of solving this problem is by drawing a Venn diagram based on what is known:
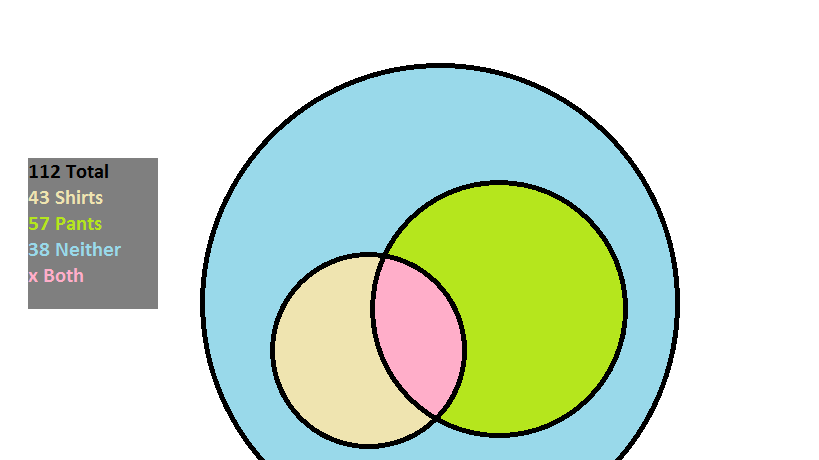
There are  customers; within them there are those that purchased something (pants, shirts, or possibly a combination), and those that purchased nothing.
customers; within them there are those that purchased something (pants, shirts, or possibly a combination), and those that purchased nothing.
The amount of individuals that purchased something is given as:

The reason that the number of shoppers that bought both is subtracted is so that it is not counted twice when the customers that bought pants and the customers that bought shirts are added together.
Since  bought nothing,
bought nothing,

The amount that bought both then is:


A way of solving this problem is by drawing a Venn diagram based on what is known:

There are 
The amount of individuals that purchased something is given as:
The reason that the number of shoppers that bought both is subtracted is so that it is not counted twice when the customers that bought pants and the customers that bought shirts are added together.
Since 
The amount that bought both then is:
Compare your answer with the correct one above
In a school, 70 students are taking classes. 35 of them will be taking Accounting and 20 of them will be taking Economics. 7 of them are taking both of these classes. How many of the students are not in either class?
In a school, 70 students are taking classes. 35 of them will be taking Accounting and 20 of them will be taking Economics. 7 of them are taking both of these classes. How many of the students are not in either class?
When you add both class rosters you get a total of 55 students
 .
.
You must subtract the 7 that are in both because they are counted twice in the 55
 .
.
The total in neither class will be the total students minus the adjusted enrollment in both classes
 .
.
When you add both class rosters you get a total of 55 students

You must subtract the 7 that are in both because they are counted twice in the 55

The total in neither class will be the total students minus the adjusted enrollment in both classes

Compare your answer with the correct one above
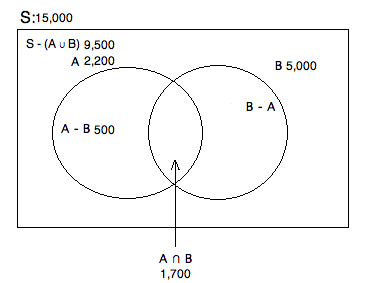
There are 15,000 students at college X. Of those students, 1,700 are taking both ethics and metaphysics this semester. There are 2,200 total students taking ethics. 9,500 students are taking neither of these classes. How many students are taking metaphysics this term?
There are 15,000 students at college X. Of those students, 1,700 are taking both ethics and metaphysics this semester. There are 2,200 total students taking ethics. 9,500 students are taking neither of these classes. How many students are taking metaphysics this term?
The easiest way to understand this problem is to draw a Venn Diagram:
S = Total number of students
A = Total students taking ethics
B = Total students taking metaphysics
A - B = Students taking only ethics
B - A = Students taking only metaphysics
A ∪ B = The total students taking either ethics or metaphysics
A ∩ B = The total students taking both ethics and metaphysics
We know there are 15,000 total and that 9,500 are taking neither class. Therefore, we know that 15,000 - 9,500 = 5,500 are taking at least one of the classes. Based on our prompt, we know that there are 1,700 taking both and that 2,200 are taking ethics. To fiind out how many are taking ONLY ethics, we have to subtract off the amount that are taking ethics and metaphysics. Hence, 2,200 - 1,700 = 500. Finally, if we know that there are 5,500 taking at at least one of these classes, we want to get rid of that portion taking ethics. This will leave us with those who are taking at least metaphysics (regardless of whether or not they are taking ethics): 5,500 - 500 = 5,000.
The easiest way to understand this problem is to draw a Venn Diagram:
S = Total number of students
A = Total students taking ethics
B = Total students taking metaphysics
A - B = Students taking only ethics
B - A = Students taking only metaphysics
A ∪ B = The total students taking either ethics or metaphysics
A ∩ B = The total students taking both ethics and metaphysics
We know there are 15,000 total and that 9,500 are taking neither class. Therefore, we know that 15,000 - 9,500 = 5,500 are taking at least one of the classes. Based on our prompt, we know that there are 1,700 taking both and that 2,200 are taking ethics. To fiind out how many are taking ONLY ethics, we have to subtract off the amount that are taking ethics and metaphysics. Hence, 2,200 - 1,700 = 500. Finally, if we know that there are 5,500 taking at at least one of these classes, we want to get rid of that portion taking ethics. This will leave us with those who are taking at least metaphysics (regardless of whether or not they are taking ethics): 5,500 - 500 = 5,000.
Compare your answer with the correct one above
In a class of 100 students, 43 play basketball and 37 play baseball. 9 students play both. How many students do not play either sport?
In a class of 100 students, 43 play basketball and 37 play baseball. 9 students play both. How many students do not play either sport?
In order to determine how many students are not enrolled in a sport, we must first determine how many students are. The simplest way to do this is to begin by adding the students of both sports together.
43 + 37 = 80
But wait! 9 of those students are play both baseball and basketball. To avoid double counting these students, subtract 9 from the total.
80 – 9 = 71
Now we know 71 students play sports. If there are 100 students, all that's left to do is subtract.
100 – 71 = 29
29 students do not play basketball or baseball.
In order to determine how many students are not enrolled in a sport, we must first determine how many students are. The simplest way to do this is to begin by adding the students of both sports together.
43 + 37 = 80
But wait! 9 of those students are play both baseball and basketball. To avoid double counting these students, subtract 9 from the total.
80 – 9 = 71
Now we know 71 students play sports. If there are 100 students, all that's left to do is subtract.
100 – 71 = 29
29 students do not play basketball or baseball.
Compare your answer with the correct one above