Plane Geometry - GRE Quantitative Reasoning
Card 0 of 1504
Quantitative Comparison

Column A
Area
Column B
Perimeter
Quantitative Comparison

Column A
Area
Column B
Perimeter
To find the perimeter, add up the sides, here 5 + 12 + 13 = 30. To find the area, multiply the two legs together and divide by 2, here (5 * 12)/2 = 30.
To find the perimeter, add up the sides, here 5 + 12 + 13 = 30. To find the area, multiply the two legs together and divide by 2, here (5 * 12)/2 = 30.
Compare your answer with the correct one above

Given triangle ACE where B is the midpoint of AC, what is the area of triangle ABD?

Given triangle ACE where B is the midpoint of AC, what is the area of triangle ABD?
If B is a midpoint of AC, then we know AB is 12. Moreover, triangles ACE and ABD share angle DAB and have right angles which makes them similar triangles. Thus, their sides will all be proportional, and BD is 4. 1/2bh gives us 1/2 * 12 * 4, or 24.
If B is a midpoint of AC, then we know AB is 12. Moreover, triangles ACE and ABD share angle DAB and have right angles which makes them similar triangles. Thus, their sides will all be proportional, and BD is 4. 1/2bh gives us 1/2 * 12 * 4, or 24.
Compare your answer with the correct one above
What is the area of a right triangle with hypotenuse of 13 and base of 12?
What is the area of a right triangle with hypotenuse of 13 and base of 12?
Area = 1/2(base)(height). You could use Pythagorean theorem to find the height or, if you know the special right triangles, recognize the 5-12-13. The area = 1/2(12)(5) = 30.
Area = 1/2(base)(height). You could use Pythagorean theorem to find the height or, if you know the special right triangles, recognize the 5-12-13. The area = 1/2(12)(5) = 30.
Compare your answer with the correct one above
Quantitative Comparison
Quantity A: the area of a right triangle with sides 10, 24, 26
Quantity B: twice the area of a right triangle with sides 5, 12, 13
Quantitative Comparison
Quantity A: the area of a right triangle with sides 10, 24, 26
Quantity B: twice the area of a right triangle with sides 5, 12, 13
Quantity A: area = base * height / 2 = 10 * 24 / 2 = 120
Quantity B: 2 * area = 2 * base * height / 2 = base * height = 5 * 12 = 60
Therefore Quantity A is greater.
Quantity A: area = base * height / 2 = 10 * 24 / 2 = 120
Quantity B: 2 * area = 2 * base * height / 2 = base * height = 5 * 12 = 60
Therefore Quantity A is greater.
Compare your answer with the correct one above
Quantitative Comparison
Quantity A: The area of a triangle with a height of 6 and a base of 7
Quantity B: Half the area of a trapezoid with a height of 6, a base of 6, and another base of 10
Quantitative Comparison
Quantity A: The area of a triangle with a height of 6 and a base of 7
Quantity B: Half the area of a trapezoid with a height of 6, a base of 6, and another base of 10
Quantity A: Area = 1/2 * b * h = 1/2 * 6 * 7 = 42/2 = 21
Quantity B: Area = 1/2 * (_b_1 + _b_2) * h = 1/2 * (6 + 10) * 6 = 48
Half of the area = 48/2 = 24
Quantity B is greater.
Quantity A: Area = 1/2 * b * h = 1/2 * 6 * 7 = 42/2 = 21
Quantity B: Area = 1/2 * (_b_1 + _b_2) * h = 1/2 * (6 + 10) * 6 = 48
Half of the area = 48/2 = 24
Quantity B is greater.
Compare your answer with the correct one above
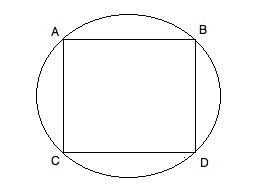
If the area of the square is 9, then s2 = 9 and s = 3. If the sides thus equal 3, we can calculate the diagonals (either CB or AD) by using the 45-45-90 triangle ratio. For a side of 3, the diagonal will be 3√(2). Note that since the square is inscribed in the circle, this diagonal is also the diameter of the circle. If it is such, the radius is one half of that or 1.5√(2).
Based on that value, we can computer the circle’s area:
A = πr2 = π(1.5√(2))2 = (2.25 * 2)π = 4.5π
If the area of the square is 9, then s2 = 9 and s = 3. If the sides thus equal 3, we can calculate the diagonals (either CB or AD) by using the 45-45-90 triangle ratio. For a side of 3, the diagonal will be 3√(2). Note that since the square is inscribed in the circle, this diagonal is also the diameter of the circle. If it is such, the radius is one half of that or 1.5√(2).
Based on that value, we can computer the circle’s area:
A = πr2 = π(1.5√(2))2 = (2.25 * 2)π = 4.5π
Compare your answer with the correct one above
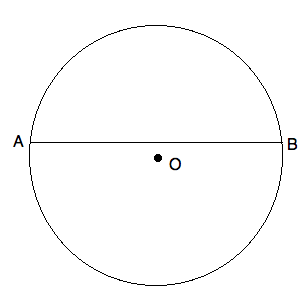
"O" is the center of the circle as shown below.

A
---
The radius of the circle
B
---
3
"O" is the center of the circle as shown below.
A
---
The radius of the circle
B
---
3
We know the triangle inscribed within the circle must be isosceles, as it contains a 90-degree angle and fixed radii. As such, the opposite angles must be equal. Therefore we can use a simplified version of the Pythagorean Theorem,
a2 + a2 = c2 → 2r2 = 16 → r2 = 8; r = √8 < 3. (since we know √9 = 3, we know √8 must be less); therefore, Quantity B is greater.
We know the triangle inscribed within the circle must be isosceles, as it contains a 90-degree angle and fixed radii. As such, the opposite angles must be equal. Therefore we can use a simplified version of the Pythagorean Theorem,
a2 + a2 = c2 → 2r2 = 16 → r2 = 8; r = √8 < 3. (since we know √9 = 3, we know √8 must be less); therefore, Quantity B is greater.
Compare your answer with the correct one above
Which point could lie on the circle with radius 5 and center (1,2)?
Which point could lie on the circle with radius 5 and center (1,2)?
A radius of 5 means we need a distance of 5 from the center to any points on the circle. We need 52 = (1 – _x_2)2 + (2 – _y_2)2. Let's start with the first point, (3,4). (1 – 3)2 + (2 – 4)2 ≠ 25. Next let's try (4,6). (1 – 4)2 + (2 – 6)2 = 25, so (4,6) is our answer. The same can be done for the other three points to prove they are incorrect answers, but this is something to do ONLY if you have enough time.
A radius of 5 means we need a distance of 5 from the center to any points on the circle. We need 52 = (1 – _x_2)2 + (2 – _y_2)2. Let's start with the first point, (3,4). (1 – 3)2 + (2 – 4)2 ≠ 25. Next let's try (4,6). (1 – 4)2 + (2 – 6)2 = 25, so (4,6) is our answer. The same can be done for the other three points to prove they are incorrect answers, but this is something to do ONLY if you have enough time.
Compare your answer with the correct one above
O is the center of the circle above.
The length of  is
is  .
.
Quantity A: The area of the circle.
Quantity B: 
Which of the following is true?

O is the center of the circle above.
The length of 

Quantity A: The area of the circle.
Quantity B:
Which of the following is true?

O is the center of the circle above.
The length of  is
is  .
.
Quantity A: The area of the circle.
Quantity B: 
Do not be tricked by this question. It is true that  can be split into halves, each of which are
can be split into halves, each of which are  in length. These halves are not, however, radii to the circle. Since this does not go through the center of the circle, its length is shorter than the diameter. This means that the radius of the circle must be greater than
in length. These halves are not, however, radii to the circle. Since this does not go through the center of the circle, its length is shorter than the diameter. This means that the radius of the circle must be greater than  . Now, if it were
. Now, if it were  , the area would be
, the area would be  . Since it is larger than
. Since it is larger than  , the area must be larger than
, the area must be larger than  . Quantity A is larger than quantity B.
. Quantity A is larger than quantity B.

O is the center of the circle above.
The length of 

Quantity A: The area of the circle.
Quantity B:
Do not be tricked by this question. It is true that 






Compare your answer with the correct one above

O is the center of the circle above.
The circumference of the circle above is  .
.
Quantity A: The length of 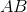 .
.
Quantity B: 
Which of the following is true?

O is the center of the circle above.
The circumference of the circle above is 
Quantity A: The length of 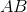
Quantity B:
Which of the following is true?
Now, we know that the circumference of a circle is:
 or
or 
This means that the diameter of our circle is must be  . Given this, we know that the
. Given this, we know that the  must be shorter than
must be shorter than  , for the diameter is the longer than any chord that does not pass through the center of the circle. Quantity B is larger than quantity A.
, for the diameter is the longer than any chord that does not pass through the center of the circle. Quantity B is larger than quantity A.
Now, we know that the circumference of a circle is:

This means that the diameter of our circle is must be 


Compare your answer with the correct one above
What is the circumference of a circle with an area of 36π?
What is the circumference of a circle with an area of 36π?
We know that the area of a circle can be expressed: a = πr2
If we know that the area is 36π, we can substitute this into said equation and get: 36π = πr2
Solving for r, we get: 36 = r2; (after taking the square root of both sides:) 6 = r
Now, we know that the circuference of a circle is expressed: c = πd. Since we know that d = 2r (two radii, placed one after the other, make a diameter), we can rewrite the circumference equation to be: c = 2πr
Since we have r, we can rewrite this to be: c = 2π*6 = 12π
We know that the area of a circle can be expressed: a = πr2
If we know that the area is 36π, we can substitute this into said equation and get: 36π = πr2
Solving for r, we get: 36 = r2; (after taking the square root of both sides:) 6 = r
Now, we know that the circuference of a circle is expressed: c = πd. Since we know that d = 2r (two radii, placed one after the other, make a diameter), we can rewrite the circumference equation to be: c = 2πr
Since we have r, we can rewrite this to be: c = 2π*6 = 12π
Compare your answer with the correct one above
Circle A has an area of  . What is the perimeter of an enclosed semi-circle with half the radius of circle A?
. What is the perimeter of an enclosed semi-circle with half the radius of circle A?
Circle A has an area of 
Based on our information, we know that the 121π = πr2; 121 = r2; r = 11.
Our other circle with half the radius of A has a diameter equal to the radius of A. Therefore, the circumference of this circle is 11π. Half of this is 5.5π. However, since this is a semi circle, it is enclosed and looks like this:
Therefore, we have to include the diameter in the perimeter. Therefore, the total perimeter of the semi-circle is 5.5π + 11.
Based on our information, we know that the 121π = πr2; 121 = r2; r = 11.
Our other circle with half the radius of A has a diameter equal to the radius of A. Therefore, the circumference of this circle is 11π. Half of this is 5.5π. However, since this is a semi circle, it is enclosed and looks like this:
Therefore, we have to include the diameter in the perimeter. Therefore, the total perimeter of the semi-circle is 5.5π + 11.
Compare your answer with the correct one above
Which is greater: the circumference of a circle with an area of  , or the perimeter of a square with side length
, or the perimeter of a square with side length  inches?
inches?
Which is greater: the circumference of a circle with an area of 

Starting with the circle, we need to find the radius in order to get the circumference. Find r by plugging our given area into the equation for the area of a circle:
A = pi $r^2$
25pi = pi $r^2$
25 = $r^2$

Then calculate circumference:
C = 2pi r
C = 2pi times 5 = 10pi approx 31.4 inches (approximating pi as 3.14)
To find the perimeter of the square, we can use P = 4s , where P is the perimeter and s is the side length:

31.4>28, so the circle's circumference is greater.
Starting with the circle, we need to find the radius in order to get the circumference. Find r by plugging our given area into the equation for the area of a circle:
A = pi $r^2$
25pi = pi $r^2$
25 = $r^2$
Then calculate circumference:
C = 2pi r
C = 2pi times 5 = 10pi approx 31.4 inches (approximating pi as 3.14)
To find the perimeter of the square, we can use P = 4s , where P is the perimeter and s is the side length:
31.4>28, so the circle's circumference is greater.
Compare your answer with the correct one above

Quantity A: The circumference of a circle with radius 
Quantity B: The area of a circle with a diameter one fourth the radius of the circle in Quantity A
Which of the following is true?
Quantity A: The circumference of a circle with radius
Quantity B: The area of a circle with a diameter one fourth the radius of the circle in Quantity A
Which of the following is true?
Let's compute each value separately. We know that the radii are positive numbers that are greater than or equal to  . This means that we do not need to worry about the fact that the area could represent a square of a decimal value like
. This means that we do not need to worry about the fact that the area could represent a square of a decimal value like  .
.
Quantity A
Since  , we know:
, we know:

Quantity B
If the diameter is one-fourth the radius of A, we know:

Thus, the radius must be half of that, or  .
.
Now, we need to compute the area of this circle. We know:

Therefore, 
Now, notice that if  , Quantity A is larger.
, Quantity A is larger.
However, if we choose a value like  , we have:
, we have:
Quantity A: 
Quantity B: 
Therefore, the relation cannot be determined!
Let's compute each value separately. We know that the radii are positive numbers that are greater than or equal to 

Quantity A
Since 
Quantity B
If the diameter is one-fourth the radius of A, we know:
Thus, the radius must be half of that, or 
Now, we need to compute the area of this circle. We know:
Therefore,
Now, notice that if 
However, if we choose a value like 
Quantity A:
Quantity B:
Therefore, the relation cannot be determined!
Compare your answer with the correct one above

Circle  has a center in the center of Square
has a center in the center of Square  .
.
The area of Square  is
is 
 .
.
What is the circumference of Circle  ?
?

Circle 

The area of Square 


What is the circumference of Circle 
Since we know that the area of Square  is
is  , we know
, we know  , where
, where  is the length of one of its sides. From this, we can solve for
is the length of one of its sides. From this, we can solve for  by taking the square root of both sides. You will have to do this by estimating upward. Therefore, you know that
by taking the square root of both sides. You will have to do this by estimating upward. Therefore, you know that  is
is  . By careful guessing, you can quickly see that
. By careful guessing, you can quickly see that  is
is  . From this, you know that the diameter of your circle must be half of
. From this, you know that the diameter of your circle must be half of  , or
, or  (because it is circumscribed). Therefore, you can draw:
(because it is circumscribed). Therefore, you can draw:

The circumference of this circle is defined as:
 or, for your values:
or, for your values:

(You could also compute this from the diameter, but many students just memorize the formula above.)
Since we know that the area of Square 











The circumference of this circle is defined as:

(You could also compute this from the diameter, but many students just memorize the formula above.)
Compare your answer with the correct one above
What is the area of a circle, one-quarter of the circumference of which is 5.5 inches?
What is the area of a circle, one-quarter of the circumference of which is 5.5 inches?
Here, you need to “solve backward” from the data you have been given. We know that 0.25C = 5.5; therefore, C = 22. In order to solve for the area, we will need the radius of the circle. This can be obtained by recalling that C = 2πr. Replacing 22 for C, we get 22 = 2πr.
Solve for r: r = 22 / 2π = 11 / π.
Now, we solve for the area: A = πr2. Replacing 11 / π for r: A = π (11 / π)2 = (121π) / (π2) = 121 / π.
Here, you need to “solve backward” from the data you have been given. We know that 0.25C = 5.5; therefore, C = 22. In order to solve for the area, we will need the radius of the circle. This can be obtained by recalling that C = 2πr. Replacing 22 for C, we get 22 = 2πr.
Solve for r: r = 22 / 2π = 11 / π.
Now, we solve for the area: A = πr2. Replacing 11 / π for r: A = π (11 / π)2 = (121π) / (π2) = 121 / π.
Compare your answer with the correct one above
Given circle O with a diameter of 2 and square ABCD inscribed within circle O, what is the area of the shaded region?

Given circle O with a diameter of 2 and square ABCD inscribed within circle O, what is the area of the shaded region?

There are two steps to this problem: determining the area of the circle and determining the area of the square. The area of the circle is πr2 which is π(2/1)2 or π. AD is a diameter of circle O and creates two isosceles right triangles with ACD and ABD. The relationship between sides of an isosceles right triangle is 1 : 1 : √2. Thus the sides of square ABCD are √2 and the area is 2. The area of the shaded region is the area of the circle minus the area of the square, or π – 2.
There are two steps to this problem: determining the area of the circle and determining the area of the square. The area of the circle is πr2 which is π(2/1)2 or π. AD is a diameter of circle O and creates two isosceles right triangles with ACD and ABD. The relationship between sides of an isosceles right triangle is 1 : 1 : √2. Thus the sides of square ABCD are √2 and the area is 2. The area of the shaded region is the area of the circle minus the area of the square, or π – 2.
Compare your answer with the correct one above
For  , Chelsea can get either a
, Chelsea can get either a  diameter pizza or two
diameter pizza or two  diameter pizzas. Which is the better deal?
diameter pizzas. Which is the better deal?
For 





Therefore the 16 inch pizza is the better deal.
Therefore the 16 inch pizza is the better deal.
Compare your answer with the correct one above
Circle B has a circumference of 36π. What is the area of circle A, which has a radius half the length of the radius of circle B?
Circle B has a circumference of 36π. What is the area of circle A, which has a radius half the length of the radius of circle B?
To find the radius of circle B, use the circumference formula (c = πd = 2πr):
2πr = 36π
Divide each side by 2π: r = 18
Now, if circle A has a radius half the length of that of B, A's radius is 18 / 2 = 9.
The area of a circle is πr2. Therefore, for A, it is π*92 = 81π.
To find the radius of circle B, use the circumference formula (c = πd = 2πr):
2πr = 36π
Divide each side by 2π: r = 18
Now, if circle A has a radius half the length of that of B, A's radius is 18 / 2 = 9.
The area of a circle is πr2. Therefore, for A, it is π*92 = 81π.
Compare your answer with the correct one above
A small circle with radius 5 lies inside a larger circle with radius x. What is the area of the region inside the larger circle, but outside of the smaller circle, in terms of x?
A small circle with radius 5 lies inside a larger circle with radius x. What is the area of the region inside the larger circle, but outside of the smaller circle, in terms of x?
Since the answers are in terms of pi, simply find the area of each circle in terms of x and ∏:
Smaller: ∏(5)2 = 25∏
Larger: ∏x2
We must subtract the inner circle from the outer circle; this translates to ∏x2-25∏.
Since the answers are in terms of pi, simply find the area of each circle in terms of x and ∏:
Smaller: ∏(5)2 = 25∏
Larger: ∏x2
We must subtract the inner circle from the outer circle; this translates to ∏x2-25∏.
Compare your answer with the correct one above