Operations - GRE Quantitative Reasoning
Card 0 of 168
Of a group of 335 graduating high school atheletes, 106 played basketball, 137 ran track and field, and 51 participated in swimming. What is the maximum number of students that did both track and field and swimming upon graduation?
Of a group of 335 graduating high school atheletes, 106 played basketball, 137 ran track and field, and 51 participated in swimming. What is the maximum number of students that did both track and field and swimming upon graduation?
Simply recognize that logically, the participation of either sport is non-exclusive, that is, just because people took track and field does not necessarily mean they did not take swimming as well. As such, those 51 who took swimming could have all potentially done track and field, which means all 51 students.
Simply recognize that logically, the participation of either sport is non-exclusive, that is, just because people took track and field does not necessarily mean they did not take swimming as well. As such, those 51 who took swimming could have all potentially done track and field, which means all 51 students.
Compare your answer with the correct one above
The product of two consecutive positive integers is 272. What is the larger of the two integers?
The product of two consecutive positive integers is 272. What is the larger of the two integers?
In order to multiply to 272, the units digits of the two integers will have to multiply to a number with a units digit of 2. For 17, you can see that 6 x 7 (the units digits of 16 and 17) = 42. The best strategy here is to plug in the choices using the units digit strategy.
In order to multiply to 272, the units digits of the two integers will have to multiply to a number with a units digit of 2. For 17, you can see that 6 x 7 (the units digits of 16 and 17) = 42. The best strategy here is to plug in the choices using the units digit strategy.
Compare your answer with the correct one above
Of 300 students, 120 are enrolled in math club, 150 are enrolled in chess club, and 100 are enrolled in both. How many students are not members of either club?
Of 300 students, 120 are enrolled in math club, 150 are enrolled in chess club, and 100 are enrolled in both. How many students are not members of either club?
There are 120 students in the math club and 150 students in the chess club, for a total membership of 270. However, 100 students are in both clubs, which means they are counted twice. You simply subtract 100 from 270, which will give you a total of 170 different students participating in both clubs. This means that the remaining 130 students do not participate in either club.
There are 120 students in the math club and 150 students in the chess club, for a total membership of 270. However, 100 students are in both clubs, which means they are counted twice. You simply subtract 100 from 270, which will give you a total of 170 different students participating in both clubs. This means that the remaining 130 students do not participate in either club.
Compare your answer with the correct one above
Choose the answer which best solves the following equation:

Choose the answer which best solves the following equation:
When adding integers, one needs to pay close attention to the sign. When you add a negative integer, it's the same thing as subtracting that integer. Therefore:

When adding integers, one needs to pay close attention to the sign. When you add a negative integer, it's the same thing as subtracting that integer. Therefore:
Compare your answer with the correct one above
Choose the answer below which best solves the following equation:

Choose the answer below which best solves the following equation:
The sum of any two negative numbers will be negative. Remember, also, that adding a negative number is like subtracting it. Therefore:

The sum of any two negative numbers will be negative. Remember, also, that adding a negative number is like subtracting it. Therefore:
Compare your answer with the correct one above
Which of the following integers is divisible by  ?
?
Which of the following integers is divisible by 
In order to find a number divisible by 6, you must find a number divisible by both of its factors — 2 and 3. Only even numbers are divisible by 2, so 81 is eliminated. In order to be divisible by 3, the sum of the digits has to be divisible by 3.
The sum of the digits of 316 is 3 + 1 + 6 = 10.
For 240, the sum is 2 + 4 = 6.
For 118, the sum is 1 + 1 + 8 = 10.
Only 6 is divisible by 3.
In order to find a number divisible by 6, you must find a number divisible by both of its factors — 2 and 3. Only even numbers are divisible by 2, so 81 is eliminated. In order to be divisible by 3, the sum of the digits has to be divisible by 3.
The sum of the digits of 316 is 3 + 1 + 6 = 10.
For 240, the sum is 2 + 4 = 6.
For 118, the sum is 1 + 1 + 8 = 10.
Only 6 is divisible by 3.
Compare your answer with the correct one above
Which of the following rules makes the expression  an integer?
an integer?
Which of the following rules makes the expression 
4 is already an integer, so we need to make sure x/10 is an integer too.
Multiples of 5 won't work. For example, 5 is a multiple of 5 but 5/10 isn't an integer. Similarly, if x/10 leaves a remainder of 5, x/10 isn't an integer. For example, 15/10 leaves a remainder of 5 and isn't an integer.
If x/10 has no remainder, then it must be an integer. For example, 10/10 and 20/10 both leave no remainders and simplify to the integers 1 and 2, respectively.
4 is already an integer, so we need to make sure x/10 is an integer too.
Multiples of 5 won't work. For example, 5 is a multiple of 5 but 5/10 isn't an integer. Similarly, if x/10 leaves a remainder of 5, x/10 isn't an integer. For example, 15/10 leaves a remainder of 5 and isn't an integer.
If x/10 has no remainder, then it must be an integer. For example, 10/10 and 20/10 both leave no remainders and simplify to the integers 1 and 2, respectively.
Compare your answer with the correct one above
Apples are sold by whole bushels. You cannot purchase part of a bushel. There are 126 apples in a bushel.
Sam is a caterer who needs to bake 300 pies to sell at the county fair. If it takes 4 apples to make a pie, how many bushels must Sam order to ensure he has enough apples for his pies?
Apples are sold by whole bushels. You cannot purchase part of a bushel. There are 126 apples in a bushel.
Sam is a caterer who needs to bake 300 pies to sell at the county fair. If it takes 4 apples to make a pie, how many bushels must Sam order to ensure he has enough apples for his pies?
Because Sam needs to make 300 pies, and each pie needs 4 apples, the number of apples he needs is
300 x 4 = 1200.
To determine how many bushels Sam needs, divide the total number of apples by the number of apples sold in a bushel.
1200 / 126 = 9.524
Because apples are sold by the whole bushel, Sam cannot order part of a bushel. In order to make sure he has sufficient apples, he will need to order 10 bushels.
Because Sam needs to make 300 pies, and each pie needs 4 apples, the number of apples he needs is
300 x 4 = 1200.
To determine how many bushels Sam needs, divide the total number of apples by the number of apples sold in a bushel.
1200 / 126 = 9.524
Because apples are sold by the whole bushel, Sam cannot order part of a bushel. In order to make sure he has sufficient apples, he will need to order 10 bushels.
Compare your answer with the correct one above
The remainder of  is
is  .
.
Quantity A:

Quantity B:

The remainder of 

Quantity A:
Quantity B:
If the remainder of  is
is  , we know that
, we know that  could be:
could be:

Since this generates an entire list of values, we cannot know which quantity is larger.
Do not be tricked by the question, which is trying to get you to say that they are equal!
If the remainder of 


Since this generates an entire list of values, we cannot know which quantity is larger.
Do not be tricked by the question, which is trying to get you to say that they are equal!
Compare your answer with the correct one above
The remainder of  is
is  .
.
The remainder of  is
is  .
.
Which of the following is a potential value for  ?
?
The remainder of 

The remainder of 

Which of the following is a potential value for 
Begin by writing out a few possible values for  and
and  .
.
Since the remainder of  is
is  , we can list:
, we can list:

Since the remainder of  is
is  , we can list:
, we can list:

Since  (which is
(which is  ) is your smallest possible value, you know that
) is your smallest possible value, you know that  and
and  are not options. You cannot derive either
are not options. You cannot derive either  or
or  from the values given.
from the values given.
Therefore, the only option that is left is  , which is equal to
, which is equal to  .
.
Begin by writing out a few possible values for 

Since the remainder of 

Since the remainder of 

Since 





Therefore, the only option that is left is 

Compare your answer with the correct one above
Evaluate:
3 + 2(1 * 9 + 8) – 9/3
Evaluate:
3 + 2(1 * 9 + 8) – 9/3
Order of operations
Do everything inside the parenthesis first:
3 + 2(17) – 9/3
next, do multiplication/division
3 + 34 – 3
= 34
Order of operations
Do everything inside the parenthesis first:
3 + 2(17) – 9/3
next, do multiplication/division
3 + 34 – 3
= 34
Compare your answer with the correct one above
3 + 4 * 5 / 10 – 2 =
3 + 4 * 5 / 10 – 2 =
Here we must use order of operations. First we multiply 4 * 5 = 20. Then 20 / 10 = 2. Now we can do the addition and substraction. 3 + 2 – 2 = 3. If you started at the beginning on the left hand side and not used order of operations, you would mistakenly choose 1.5 as the correct answer.
Here we must use order of operations. First we multiply 4 * 5 = 20. Then 20 / 10 = 2. Now we can do the addition and substraction. 3 + 2 – 2 = 3. If you started at the beginning on the left hand side and not used order of operations, you would mistakenly choose 1.5 as the correct answer.
Compare your answer with the correct one above
This looks daunting as one long equation, but let's look at each piece and then add them all together.
2–3 = 1/23 = 1/8
250 = 1
(–218)1 = –218
6251/4 = 5
(–27)1/3 = –3
Then, 2–3 + 250 + (–218)1 + 7/8 – 6251/4 + (–27)1/3 = 1/8 + 1 – 218 + 7/8 – 5 – 3 = –224.
This looks daunting as one long equation, but let's look at each piece and then add them all together.
2–3 = 1/23 = 1/8
250 = 1
(–218)1 = –218
6251/4 = 5
(–27)1/3 = –3
Then, 2–3 + 250 + (–218)1 + 7/8 – 6251/4 + (–27)1/3 = 1/8 + 1 – 218 + 7/8 – 5 – 3 = –224.
Compare your answer with the correct one above
Order of operations can be remembered by PEMDAS (Please Excuse My Dear Aunt Sally): Parentheses Exponents Multiplication Division Addition Subtraction.
\[7(5 + 2) – (5 * 8)\]2 =
1: Inner parentheses = \[ 7(7) – 40 \]2
2: Outer brackets = \[ 49 – 40 \]2 = 92
3: Exponents = 81
Order of operations can be remembered by PEMDAS (Please Excuse My Dear Aunt Sally): Parentheses Exponents Multiplication Division Addition Subtraction.
\[7(5 + 2) – (5 * 8)\]2 =
1: Inner parentheses = \[ 7(7) – 40 \]2
2: Outer brackets = \[ 49 – 40 \]2 = 92
3: Exponents = 81
Compare your answer with the correct one above
What is the units digit of 3,487,903 times 37,824?
What is the units digit of 3,487,903 times 37,824?
The units digit of any product depends on the units digits of the 2 numbers multiplied, which in this case is 3 and 4. Since 3times 4=12, the units digit of 3,487,903 times 37,824 is 2.
The units digit of any product depends on the units digits of the 2 numbers multiplied, which in this case is 3 and 4. Since 3times 4=12, the units digit of 3,487,903 times 37,824 is 2.
Compare your answer with the correct one above
What is the units digit of

What is the units digit of
The units digit of the product of any two numbers is the same as the units digit of the product of the two numbers' units digits. In this case, it would be the units digit of  , which is
, which is  .
.
The units digit of the product of any two numbers is the same as the units digit of the product of the two numbers' units digits. In this case, it would be the units digit of 

Compare your answer with the correct one above
Choose the answer below which best solves the following equation:

Choose the answer below which best solves the following equation:
When multiplying integers, if one of the integers is negative, your answer will be negative:
First multiply the ones digits together.

Next multiply the ones digit of the smaller number with the tens digit of the larger number to get the tens digit of the product.

Combining these two and remembering the negative sign we get our final answer:

When multiplying integers, if one of the integers is negative, your answer will be negative:
First multiply the ones digits together.
Next multiply the ones digit of the smaller number with the tens digit of the larger number to get the tens digit of the product.
Combining these two and remembering the negative sign we get our final answer:
Compare your answer with the correct one above
Choose the answer which best solves the following equation:

Choose the answer which best solves the following equation:
When multiplying integers, if both of the signs of the integers are the same (positive, or negative) then your result will be positive:
First multiply the ones digit of both numbers together. If the product is greater than ten remember to carry the one to the tens place.

Next multiply the ones digit of the smaller number with the tens digit of the larger number and add the number that was carried over.

Combine these two together to get:

When multiplying integers, if both of the signs of the integers are the same (positive, or negative) then your result will be positive:
First multiply the ones digit of both numbers together. If the product is greater than ten remember to carry the one to the tens place.
Next multiply the ones digit of the smaller number with the tens digit of the larger number and add the number that was carried over.
Combine these two together to get:
Compare your answer with the correct one above

Which store had the greatest increase in thousands of book sales between 2000 and 2010?

Which store had the greatest increase in thousands of book sales between 2000 and 2010?
Calculate the difference in thousands of sales for each store individually:
Store A: 11-6=5 thousand
Store B: 13-8=5 thousand
Store C: 12-9=3 thousand
Stores A and B both had a 5000-book increase in sales, so A and B tie.
Calculate the difference in thousands of sales for each store individually:
Store A: 11-6=5 thousand
Store B: 13-8=5 thousand
Store C: 12-9=3 thousand
Stores A and B both had a 5000-book increase in sales, so A and B tie.
Compare your answer with the correct one above
Choose the answer below which best solves the following equation:
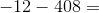
Choose the answer below which best solves the following equation:

If it helps, for this problem, think about starting at 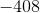 and moving twelve places in a negative direction away from zero.
and moving twelve places in a negative direction away from zero.
Also you can think to add 408 with 12 and then multiply that number by a negative one. Starting with the ones place eight plus two gives ten so we keep the zero in the ones place and carry the one to the tens place. Then we add one plus one to give us a two in the tens column. Next we have a four in the hundreds place. This gives us 420. Now we multiply this by negtive one to get our final answer of -420.
If it helps, for this problem, think about starting at 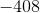
Also you can think to add 408 with 12 and then multiply that number by a negative one. Starting with the ones place eight plus two gives ten so we keep the zero in the ones place and carry the one to the tens place. Then we add one plus one to give us a two in the tens column. Next we have a four in the hundreds place. This gives us 420. Now we multiply this by negtive one to get our final answer of -420.
Compare your answer with the correct one above

![[7(5 + 2) - (5 * $8)]^2$ =](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/180401/gif.latex)