Parallel Lines - GRE Quantitative Reasoning
Card 0 of 224
Which of the following lines is parallel to:

Which of the following lines is parallel to:
First write the equation in slope intercept form. Add  to both sides to get
to both sides to get  . Now divide both sides by
. Now divide both sides by  to get
to get  . The slope of this line is
. The slope of this line is  , so any line that also has a slope of
, so any line that also has a slope of  would be parallel to it. The correct answer is
would be parallel to it. The correct answer is  .
.
First write the equation in slope intercept form. Add 






Compare your answer with the correct one above
There are two lines:
2x – 4y = 33
2x + 4y = 33
Are these lines perpendicular, parallel, non-perpendicular intersecting, or the same lines?
There are two lines:
2x – 4y = 33
2x + 4y = 33
Are these lines perpendicular, parallel, non-perpendicular intersecting, or the same lines?
To be totally clear, solve both lines in slope-intercept form:
2x – 4y = 33; –4y = 33 – 2x; y = –33/4 + 0.5x
2x + 4y = 33; 4y = 33 – 2x; y = 33/4 – 0.5x
These lines are definitely not the same. Nor are they parallel—their slopes differ. Likewise, they cannot be perpendicular (which would require not only opposite slope signs but also reciprocal slopes); therefore, they are non-perpendicular intersecting.
To be totally clear, solve both lines in slope-intercept form:
2x – 4y = 33; –4y = 33 – 2x; y = –33/4 + 0.5x
2x + 4y = 33; 4y = 33 – 2x; y = 33/4 – 0.5x
These lines are definitely not the same. Nor are they parallel—their slopes differ. Likewise, they cannot be perpendicular (which would require not only opposite slope signs but also reciprocal slopes); therefore, they are non-perpendicular intersecting.
Compare your answer with the correct one above
Which pair of linear equations represent parallel lines?
Which pair of linear equations represent parallel lines?
Parallel lines will always have equal slopes. The slope can be found quickly by observing the equation in slope-intercept form and seeing which number falls in the "m" spot in the linear equation (y=mx+b),
We are looking for an answer choice in which both equations have the same m value. Both lines in the correct answer have a slope of 2, therefore they are parallel.
Parallel lines will always have equal slopes. The slope can be found quickly by observing the equation in slope-intercept form and seeing which number falls in the "m" spot in the linear equation (y=mx+b),
We are looking for an answer choice in which both equations have the same m value. Both lines in the correct answer have a slope of 2, therefore they are parallel.
Compare your answer with the correct one above
Which of the following equations represents a line that is parallel to the line represented by the equation  ?
?
Which of the following equations represents a line that is parallel to the line represented by the equation 
Lines are parallel when their slopes are the same.
First, we need to place the given equation in the slope-intercept form.



Because the given line has the slope of  , the line parallel to it must also have the same slope.
, the line parallel to it must also have the same slope.
Lines are parallel when their slopes are the same.
First, we need to place the given equation in the slope-intercept form.
Because the given line has the slope of 
Compare your answer with the correct one above




Which of the above-listed lines are parallel?
Which of the above-listed lines are parallel?
There are several ways to solve this problem. You could solve all of the equations for  . This would give you equations in the form
. This would give you equations in the form  . All of the lines with the same
. All of the lines with the same  value would be parallel. Otherwise, you could figure out the ratio of
value would be parallel. Otherwise, you could figure out the ratio of  to
to  when both values are on the same side of the equation. This would suffice for determining the relationship between the two. We will take the first path, though, as this is most likely to be familiar to you.
when both values are on the same side of the equation. This would suffice for determining the relationship between the two. We will take the first path, though, as this is most likely to be familiar to you.
Let's solve each for  :
:












Here, you need to be a bit more manipulative with your equation. Multiply the numerator and denominator of the  value by
value by  :
:


Therefore,  ,
,  , and
, and  all have slopes of
all have slopes of 
There are several ways to solve this problem. You could solve all of the equations for 




Let's solve each for 
Here, you need to be a bit more manipulative with your equation. Multiply the numerator and denominator of the 

Therefore, 


Compare your answer with the correct one above
Which of the following is parallel to the line passing through  and
and  ?
?
Which of the following is parallel to the line passing through 

Now, notice that the slope of the line that you have been given is  . You know this because slope is merely:
. You know this because slope is merely:

However, for your points, there is no rise at all. You do not even need to compute the value. You know it will be  . All lines with slope
. All lines with slope  are of the form
are of the form  , where
, where  is the value that
is the value that  has for all
has for all  points. Based on our data, this is
points. Based on our data, this is  , for
, for  is always
is always  —no matter what is the value for
—no matter what is the value for  . So, the parallel answer choice is
. So, the parallel answer choice is  , as both have slopes of
, as both have slopes of  .
.
Now, notice that the slope of the line that you have been given is 
However, for your points, there is no rise at all. You do not even need to compute the value. You know it will be 











Compare your answer with the correct one above
Which of the following is parallel to  ?
?
Which of the following is parallel to 

To begin, solve your equation for  . This will put it into slope-intercept form, which will easily make the slope apparent. (Remember, slope-intercept form is
. This will put it into slope-intercept form, which will easily make the slope apparent. (Remember, slope-intercept form is  , where
, where  is the slope.)
is the slope.)

Divide both sides by  and you get:
and you get:

Therefore, the slope is  . Now, you need to test your points to see which set of points has a slope of
. Now, you need to test your points to see which set of points has a slope of  . Remember, for two points
. Remember, for two points  and
and  , you find the slope by using the equation:
, you find the slope by using the equation:

For our question, the pair  and
and  gives us a slope of
gives us a slope of  :
:

To begin, solve your equation for 


Divide both sides by 
Therefore, the slope is 



For our question, the pair 


Compare your answer with the correct one above
If the line through the points (5, –3) and (–2, p) is parallel to the line y = –2_x_ – 3, what is the value of p ?
If the line through the points (5, –3) and (–2, p) is parallel to the line y = –2_x_ – 3, what is the value of p ?
Since the lines are parallel, the slopes must be the same. Therefore, (p+3) divided by (_–2–_5) must equal _–_2. 11 is the only choice that makes that equation true. This can be solved by setting up the equation and solving for p, or by plugging in the other answer choices for p.





Since the lines are parallel, the slopes must be the same. Therefore, (p+3) divided by (_–2–_5) must equal _–_2. 11 is the only choice that makes that equation true. This can be solved by setting up the equation and solving for p, or by plugging in the other answer choices for p.
Compare your answer with the correct one above
What line is parallel to  and passes through the point
and passes through the point  ?
?
What line is parallel to 

Start by converting the original equation to slop-intercept form.



The slope of this line is  . A parallel line will have the same slope. Now that we know the slope of our new line, we can use slope-intercept form and the given point to solve for the y-intercept.
. A parallel line will have the same slope. Now that we know the slope of our new line, we can use slope-intercept form and the given point to solve for the y-intercept.




Plug the y-intercept into the slope-intercept equation to get the final answer.

Start by converting the original equation to slop-intercept form.
The slope of this line is 
Plug the y-intercept into the slope-intercept equation to get the final answer.
Compare your answer with the correct one above
There is a line defined by the equation below:

There is a second line that passes through the point  and is parallel to the line given above. What is the equation of this second line?
and is parallel to the line given above. What is the equation of this second line?
There is a line defined by the equation below:
There is a second line that passes through the point 
Parallel lines have the same slope. Solve for the slope in the first line by converting the equation to slope-intercept form.
3x + 4y = 12
4y = _–_3x + 12
y = –(3/4)x + 3
slope = _–_3/4
We know that the second line will also have a slope of _–_3/4, and we are given the point (1,2). We can set up an equation in slope-intercept form and use these values to solve for the y-intercept.
y = mx + b
2 = _–_3/4(1) + b
2 = _–_3/4 + b
b = 2 + 3/4 = 2.75
Plug the y-intercept back into the equation to get our final answer.
y = –(3/4)x + 2.75
Parallel lines have the same slope. Solve for the slope in the first line by converting the equation to slope-intercept form.
3x + 4y = 12
4y = _–_3x + 12
y = –(3/4)x + 3
slope = _–_3/4
We know that the second line will also have a slope of _–_3/4, and we are given the point (1,2). We can set up an equation in slope-intercept form and use these values to solve for the y-intercept.
y = mx + b
2 = _–_3/4(1) + b
2 = _–_3/4 + b
b = 2 + 3/4 = 2.75
Plug the y-intercept back into the equation to get our final answer.
y = –(3/4)x + 2.75
Compare your answer with the correct one above
What is one possible equation for a line parallel to the one passing through the points (4,2) and (15,-4)?
What is one possible equation for a line parallel to the one passing through the points (4,2) and (15,-4)?
(4,2) and (15,-4)
All that we really need to ascertain is the slope of our line. So long as a given answer has this slope, it will not matter what its y-intercept is (given the openness of our question). To find the slope, use the formula: m = rise / run = (y1 - y2) / (x1 - x2):
(2 - (-4)) / (4 - 15) = (2 + 4) / -11 = -6/11
Given this slope, our answer is: y = -6/11x + 57.4
(4,2) and (15,-4)
All that we really need to ascertain is the slope of our line. So long as a given answer has this slope, it will not matter what its y-intercept is (given the openness of our question). To find the slope, use the formula: m = rise / run = (y1 - y2) / (x1 - x2):
(2 - (-4)) / (4 - 15) = (2 + 4) / -11 = -6/11
Given this slope, our answer is: y = -6/11x + 57.4
Compare your answer with the correct one above
What line is parallel to  at
at  ?
?
What line is parallel to 

Find the slope of the given line:  (slope intercept form)
(slope intercept form)
 therefore the slope is
therefore the slope is 
Parallel lines have the same slope, so now we need to find the equation of a line with slope  and going through point
and going through point  by substituting values into the point-slope formula.
by substituting values into the point-slope formula.

So, 
Thus, the new equation is 
Find the slope of the given line: 

Parallel lines have the same slope, so now we need to find the equation of a line with slope 

So,
Thus, the new equation is
Compare your answer with the correct one above
Lines m and n are parallel

What is the value of angle  ?
?
Lines m and n are parallel
What is the value of angle 
By using the complementary and supplementary rules of geometry (due to lines m and n being parallel), as well as the fact that the sum of all angles within a triangle is 180, we can carry through the operations through stepwise subtraction of 180.
x = 125 → angle directly below also = 125. Since a line is 180 degrees, 180 – 125 = 55. Since right triangle, 90 + 55 = 145 → rightmost angle of triangle 180 – 145 = 35 which is equal to the reflected angle. Use supplementary rule again for 180 – 35 = 145 = y.
Once can also recognize that both a straight line and triangle must sum up to 180 degrees to skip the last step.
By using the complementary and supplementary rules of geometry (due to lines m and n being parallel), as well as the fact that the sum of all angles within a triangle is 180, we can carry through the operations through stepwise subtraction of 180.
x = 125 → angle directly below also = 125. Since a line is 180 degrees, 180 – 125 = 55. Since right triangle, 90 + 55 = 145 → rightmost angle of triangle 180 – 145 = 35 which is equal to the reflected angle. Use supplementary rule again for 180 – 35 = 145 = y.
Once can also recognize that both a straight line and triangle must sum up to 180 degrees to skip the last step.
Compare your answer with the correct one above
What is the equation of a line that is parallel to  and passes through
and passes through  ?
?
What is the equation of a line that is parallel to 

To solve, we will need to find the slope of the line. We know that it is parallel to the line given by the equation, meaning that the two lines will have equal slopes. Find the slope of the given line by converting the equation to slope-intercept form.



The slope of the line will be  . In slope intercept-form, we know that the line will be
. In slope intercept-form, we know that the line will be  . Now we can use the given point to find the y-intercept.
. Now we can use the given point to find the y-intercept.




The final equation for the line will be  .
.
To solve, we will need to find the slope of the line. We know that it is parallel to the line given by the equation, meaning that the two lines will have equal slopes. Find the slope of the given line by converting the equation to slope-intercept form.
The slope of the line will be 

The final equation for the line will be 
Compare your answer with the correct one above
What is the equation of a line that is parallel to the line y=\frac{1}{2}$x+3 and includes the point  ?
?
What is the equation of a line that is parallel to the line y=\frac{1}{2}$x+3 and includes the point 
The line parallel to y=\frac{1}{2}$x+3 must have a slope of $\frac{1}{2}$, giving us the equation y=\frac{1}{2}$x+b. To solve for b, we can substitute the values for y and x.
2=($\frac{1}{2}$)(4)+b
2=2+b
b=0
Therefore, the equation of the line is y=\frac{1}{2}$x.
The line parallel to y=\frac{1}{2}$x+3 must have a slope of $\frac{1}{2}$, giving us the equation y=\frac{1}{2}$x+b. To solve for b, we can substitute the values for y and x.
2=($\frac{1}{2}$)(4)+b
2=2+b
b=0
Therefore, the equation of the line is y=\frac{1}{2}$x.
Compare your answer with the correct one above
What line is parallel to  , and passes through the point
, and passes through the point  ?
?
What line is parallel to 

Converting the given line to slope-intercept form we get the following equation:

For parallel lines, the slopes must be equal, so the slope of the new line must also be  . We can plug the new slope and the given point into the slope-intercept form to solve for the y-intercept of the new line.
. We can plug the new slope and the given point into the slope-intercept form to solve for the y-intercept of the new line.




Use the y-intercept in the slope-intercept equation to find the final answer.

Converting the given line to slope-intercept form we get the following equation:
For parallel lines, the slopes must be equal, so the slope of the new line must also be 
Use the y-intercept in the slope-intercept equation to find the final answer.
Compare your answer with the correct one above
Which of these formulas could be a formula for a line perpendicular to the line  ?
?
Which of these formulas could be a formula for a line perpendicular to the line 
This is a two-step problem. First, the slope of the original line needs to be found. The slope will be represented by " " when the line is in
" when the line is in  -intercept form
-intercept form  .
.



So the slope of the original line is  . A line with perpendicular slope will have a slope that is the inverse reciprocal of the original. So in this case, the slope would be
. A line with perpendicular slope will have a slope that is the inverse reciprocal of the original. So in this case, the slope would be  . The second step is finding which line will give you that slope. For the correct answer, we find the following:
. The second step is finding which line will give you that slope. For the correct answer, we find the following:



So, the slope is  , and this line is perpendicular to the original.
, and this line is perpendicular to the original.
This is a two-step problem. First, the slope of the original line needs to be found. The slope will be represented by "


So the slope of the original line is 

So, the slope is 
Compare your answer with the correct one above
What is the equation for the line running through  and parallel to
and parallel to  ?
?
What is the equation for the line running through 

To begin, solve the given equation for  . This will give you the slope-intercept form of the line.
. This will give you the slope-intercept form of the line.

Divide everything by  :
:

Therefore, the slope of the line is  .
.
Now, for a point  , the point-slope form of a line is:
, the point-slope form of a line is:
 , where
, where  is the slope
is the slope
For our point, this is:

Distribute and solve for  :
:


To begin, solve the given equation for 
Divide everything by 
Therefore, the slope of the line is 
Now, for a point 


For our point, this is:
Distribute and solve for 
Compare your answer with the correct one above
What is the equation for the line running through  and parallel to
and parallel to  ?
?
What is the equation for the line running through 

To begin, solve the given equation for  . This will give you the slope-intercept form of the line.
. This will give you the slope-intercept form of the line.

Divide everything by 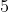 :
:

Therefore, the slope of the line is  .
.
Now, for a point  , the point-slope form of a line is:
, the point-slope form of a line is:
 , where
, where  is the slope
is the slope
For our point, this is:

This is the same as:

Distribute and solve for  :
:


To begin, solve the given equation for 
Divide everything by :
Therefore, the slope of the line is 
Now, for a point 


For our point, this is:
This is the same as:
Distribute and solve for 
Compare your answer with the correct one above
Which of the following is parallel to the line running through the points  and
and  ?
?
Which of the following is parallel to the line running through the points 

To begin, it is necessary to find the slope of the line running through the two points. (A parallel line will have the same slope. Recall that the slope is:

Or, for two points  and
and  :
:

For our points this is:

Now, to solve for this problem, the easiest way is to solve each equation for the form  . When you do this, the slope (
. When you do this, the slope ( ) will be very easy to calculate. The only option that reduces to the correct slope is
) will be very easy to calculate. The only option that reduces to the correct slope is 
Notice what happens when you solve for  :
:


This shows that the slope of this line is  .
.
To begin, it is necessary to find the slope of the line running through the two points. (A parallel line will have the same slope. Recall that the slope is:
Or, for two points 

For our points this is:
Now, to solve for this problem, the easiest way is to solve each equation for the form 

Notice what happens when you solve for 
This shows that the slope of this line is 
Compare your answer with the correct one above




