Triangles - GRE Quantitative Reasoning
Card 0 of 552
Quantitative Comparison

Column A
Area
Column B
Perimeter
Quantitative Comparison

Column A
Area
Column B
Perimeter
To find the perimeter, add up the sides, here 5 + 12 + 13 = 30. To find the area, multiply the two legs together and divide by 2, here (5 * 12)/2 = 30.
To find the perimeter, add up the sides, here 5 + 12 + 13 = 30. To find the area, multiply the two legs together and divide by 2, here (5 * 12)/2 = 30.
Compare your answer with the correct one above

Given triangle ACE where B is the midpoint of AC, what is the area of triangle ABD?

Given triangle ACE where B is the midpoint of AC, what is the area of triangle ABD?
If B is a midpoint of AC, then we know AB is 12. Moreover, triangles ACE and ABD share angle DAB and have right angles which makes them similar triangles. Thus, their sides will all be proportional, and BD is 4. 1/2bh gives us 1/2 * 12 * 4, or 24.
If B is a midpoint of AC, then we know AB is 12. Moreover, triangles ACE and ABD share angle DAB and have right angles which makes them similar triangles. Thus, their sides will all be proportional, and BD is 4. 1/2bh gives us 1/2 * 12 * 4, or 24.
Compare your answer with the correct one above
What is the area of a right triangle with hypotenuse of 13 and base of 12?
What is the area of a right triangle with hypotenuse of 13 and base of 12?
Area = 1/2(base)(height). You could use Pythagorean theorem to find the height or, if you know the special right triangles, recognize the 5-12-13. The area = 1/2(12)(5) = 30.
Area = 1/2(base)(height). You could use Pythagorean theorem to find the height or, if you know the special right triangles, recognize the 5-12-13. The area = 1/2(12)(5) = 30.
Compare your answer with the correct one above
Quantitative Comparison
Quantity A: the area of a right triangle with sides 10, 24, 26
Quantity B: twice the area of a right triangle with sides 5, 12, 13
Quantitative Comparison
Quantity A: the area of a right triangle with sides 10, 24, 26
Quantity B: twice the area of a right triangle with sides 5, 12, 13
Quantity A: area = base * height / 2 = 10 * 24 / 2 = 120
Quantity B: 2 * area = 2 * base * height / 2 = base * height = 5 * 12 = 60
Therefore Quantity A is greater.
Quantity A: area = base * height / 2 = 10 * 24 / 2 = 120
Quantity B: 2 * area = 2 * base * height / 2 = base * height = 5 * 12 = 60
Therefore Quantity A is greater.
Compare your answer with the correct one above
Quantitative Comparison
Quantity A: The area of a triangle with a height of 6 and a base of 7
Quantity B: Half the area of a trapezoid with a height of 6, a base of 6, and another base of 10
Quantitative Comparison
Quantity A: The area of a triangle with a height of 6 and a base of 7
Quantity B: Half the area of a trapezoid with a height of 6, a base of 6, and another base of 10
Quantity A: Area = 1/2 * b * h = 1/2 * 6 * 7 = 42/2 = 21
Quantity B: Area = 1/2 * (_b_1 + _b_2) * h = 1/2 * (6 + 10) * 6 = 48
Half of the area = 48/2 = 24
Quantity B is greater.
Quantity A: Area = 1/2 * b * h = 1/2 * 6 * 7 = 42/2 = 21
Quantity B: Area = 1/2 * (_b_1 + _b_2) * h = 1/2 * (6 + 10) * 6 = 48
Half of the area = 48/2 = 24
Quantity B is greater.
Compare your answer with the correct one above
Triangle BAT is defined by the coordinates (0,1), (0,7), and (8,1). What is the perimeter of triangle BAT?
Triangle BAT is defined by the coordinates (0,1), (0,7), and (8,1). What is the perimeter of triangle BAT?
These three points form a right triangle on the Cartesian coordinate system. The perimeter is comprised of the length from B to A (7-1=6); the length from B to T (8-0=8); and the length of the hypotenuse between A and T $($\sqrt{(6^{2}$$$+8^{2}$)} = 10.
The perimeter is 6+8+10=24.
These three points form a right triangle on the Cartesian coordinate system. The perimeter is comprised of the length from B to A (7-1=6); the length from B to T (8-0=8); and the length of the hypotenuse between A and T $($\sqrt{(6^{2}$$$+8^{2}$)} = 10.
The perimeter is 6+8+10=24.
Compare your answer with the correct one above
An isosceles triangle has an angle of 110°. Which of the following angles could also be in the triangle?
An isosceles triangle has an angle of 110°. Which of the following angles could also be in the triangle?
An isosceles triangle always has two equal angles. As there cannot be another 110° (the triangle cannot have over 180° total), the other two angles must equal eachother. 180° - 110° = 70°. 70° represents the other two angles, so it needs to be divided in 2 to get the answer of 35°.
An isosceles triangle always has two equal angles. As there cannot be another 110° (the triangle cannot have over 180° total), the other two angles must equal eachother. 180° - 110° = 70°. 70° represents the other two angles, so it needs to be divided in 2 to get the answer of 35°.
Compare your answer with the correct one above
An isosceles triangle ABC is laid flat on its base. Given that <B, located in the lower left corner, is 84 degrees, what is the measurement of the top angle, <A?
An isosceles triangle ABC is laid flat on its base. Given that <B, located in the lower left corner, is 84 degrees, what is the measurement of the top angle, <A?
Since the triangle is isosceles, and <A is located at the top of the triangle that is on its base, <B and <C are equivalent. Since <B is 84 degrees, <C is also. There are 180 degrees in a triangle so 180 - 84 - 84 = 12 degrees.
Since the triangle is isosceles, and <A is located at the top of the triangle that is on its base, <B and <C are equivalent. Since <B is 84 degrees, <C is also. There are 180 degrees in a triangle so 180 - 84 - 84 = 12 degrees.
Compare your answer with the correct one above

Triangle ABC is isosceles
x and y are positive integers
A
---
x
B
---
y
Triangle ABC is isosceles
x and y are positive integers
A
---
x
B
---
y
Since we are given expressions for the two congruent angles of the isosceles triangle, we can set the expressions equal to see how x relates to y. We get,
x – 3 = y – 7 --> y = x + 4
Logically, y must be the greater number if it takes x an additional 4 units to reach its value (knowing they are both positive integers).
Since we are given expressions for the two congruent angles of the isosceles triangle, we can set the expressions equal to see how x relates to y. We get,
x – 3 = y – 7 --> y = x + 4
Logically, y must be the greater number if it takes x an additional 4 units to reach its value (knowing they are both positive integers).
Compare your answer with the correct one above
An isosceles triangle has one obtuse angle that is  . What is the value of one of the other angles?
. What is the value of one of the other angles?
An isosceles triangle has one obtuse angle that is 
We know that an isosceles triangel has two equal sides and thus two equal angles opposite those equal sides. Because there is one obtuse angle of 112 degrees we automatically know that this angle is the vertex. If you sum any triangle's interior angles, you always get 180 degrees.
180 – 112 = 68 degrees. Thus there are 68 degrees left for the two equal angles. Each angle must therefore measure 34 degrees.

We know that an isosceles triangel has two equal sides and thus two equal angles opposite those equal sides. Because there is one obtuse angle of 112 degrees we automatically know that this angle is the vertex. If you sum any triangle's interior angles, you always get 180 degrees.
180 – 112 = 68 degrees. Thus there are 68 degrees left for the two equal angles. Each angle must therefore measure 34 degrees.

Compare your answer with the correct one above
What is the perimeter of an isosceles triangle given that the sides 5 units long and half of the base measures to 4 units?
What is the perimeter of an isosceles triangle given that the sides 5 units long and half of the base measures to 4 units?
The base of the triangle is 4 + 4 = 8 so the total perimeter is 5 + 5 + 8 = 18.
The base of the triangle is 4 + 4 = 8 so the total perimeter is 5 + 5 + 8 = 18.
Compare your answer with the correct one above
An obtuse Isosceles triangle has two sides with length  and one side length
and one side length  . The length of side
. The length of side 
 ft. If the length of
ft. If the length of  half the length of side
half the length of side  , what is the perimeter of the triangle?
, what is the perimeter of the triangle?
An obtuse Isosceles triangle has two sides with length 





By definition, an Isosceles triangle must have two equivalent side lengths. Since we are told that  ft and that the sides with length
ft and that the sides with length  are half the length of side
are half the length of side  , find the length of
, find the length of  by:
by:  and half of
and half of  . Thus, both of sides with length
. Thus, both of sides with length  must equal
must equal  ft.
ft.
Now, apply the formula:  .
.

Then, simplify the fraction/convert to mixed number fraction:

By definition, an Isosceles triangle must have two equivalent side lengths. Since we are told that 







Now, apply the formula: 
Then, simplify the fraction/convert to mixed number fraction:
Compare your answer with the correct one above
A triangle has two sides with length  and one side length
and one side length  . The length of side
. The length of side 
 yard. If the length of
yard. If the length of 
 the length of side
the length of side  , what is the perimeter of the triangle?
, what is the perimeter of the triangle?
A triangle has two sides with length 






The first step to solving this problem is that we must find the length of length  Since,
Since,  is
is  4 the length of side
4 the length of side  , use the following steps:
, use the following steps:


Now, apply the formula: 

The first step to solving this problem is that we must find the length of length 



Now, apply the formula:
Compare your answer with the correct one above
An acute Isosceles triangle has two sides with length  and one side length
and one side length  . The length of side
. The length of side 
 ft. If the length of
ft. If the length of  half the length of side
half the length of side  , what is the perimeter of the triangle?
, what is the perimeter of the triangle?
An acute Isosceles triangle has two sides with length 





This Isosceles triangle has two sides with a length of  foot and one side length that is half of the length of the two equivalent sides.
foot and one side length that is half of the length of the two equivalent sides.
To find the missing side, double the value of side  's denominator:
's denominator:
 . Thus, half of
. Thus, half of  .
.
Therefore, this triangle has two sides with lengths of  and one side length of
and one side length of  .
.
To find the perimeter, apply the formula:


 foot
foot  inches
inches
This Isosceles triangle has two sides with a length of 
To find the missing side, double the value of side 


Therefore, this triangle has two sides with lengths of 

To find the perimeter, apply the formula:


Compare your answer with the correct one above
An acute Isosceles triangle has two sides with length  and one side length
and one side length  . The length of side
. The length of side 
 . If the length of
. If the length of  half the length of side
half the length of side  , what is the perimeter of the triangle?
, what is the perimeter of the triangle?
An acute Isosceles triangle has two sides with length 





To solve this problem apply the formula:  .
.
However, first calculate the length of the missing side by:  .
.
Thus, the solution is:

To solve this problem apply the formula: 
However, first calculate the length of the missing side by: 
Thus, the solution is:
Compare your answer with the correct one above
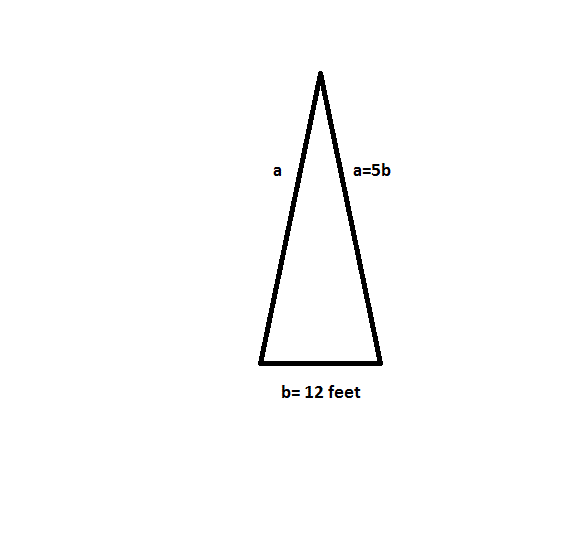
Find the perimeter of the acute Isosceles triangle shown above.
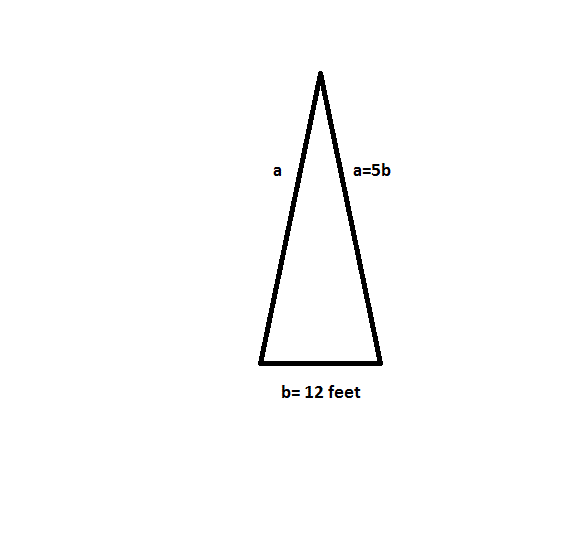
Find the perimeter of the acute Isosceles triangle shown above.
To solve this problem apply the formula:  .
.
However, first calculate the length of the missing side by:




To solve this problem apply the formula: 
However, first calculate the length of the missing side by:
Compare your answer with the correct one above
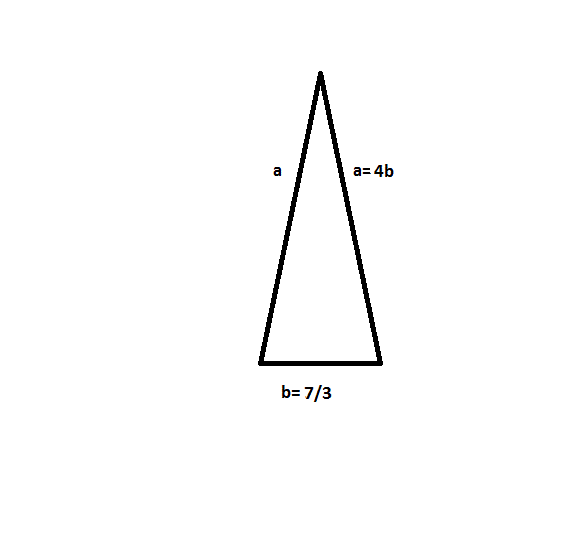
Find the perimeter of the acute Isosceles triangle shown above.
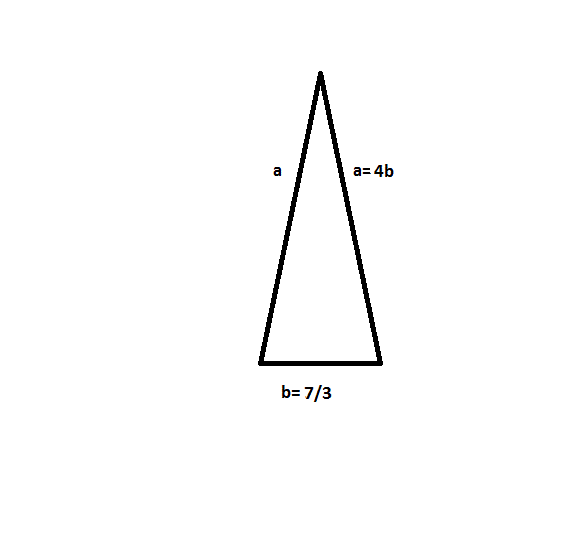
Find the perimeter of the acute Isosceles triangle shown above.
In order to solve this problem, first find the length of the missing sides. Then apply the formula: 
Each of the missing sides equal:

Then apply the perimeter formula:

In order to solve this problem, first find the length of the missing sides. Then apply the formula:
Each of the missing sides equal:
Then apply the perimeter formula:
Compare your answer with the correct one above

An acute Isosceles triangle has two sides with length  and one side length
and one side length  . The length of side
. The length of side 
 inches. If the length of
inches. If the length of 
![\sqrt[3]{a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/334904/gif.latex) , what is the perimeter of the triangle?
, what is the perimeter of the triangle?

An acute Isosceles triangle has two sides with length 




![\sqrt[3]{a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/334904/gif.latex)
In order to solve this problem, first find the length of the missing sides. Then apply the formula: 
The missing side equals:
![b=\sqrt[3]{a}=\sqrt[3]{8}=2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/334905/gif.latex)
Then plug each side length into the perimeter formula:

In order to solve this problem, first find the length of the missing sides. Then apply the formula:
The missing side equals:
Then plug each side length into the perimeter formula:
Compare your answer with the correct one above

An acute Isosceles triangle has two sides with length  and one side length
and one side length  . The length of side
. The length of side 
 inches. If the length of
inches. If the length of  , what is the perimeter of the triangle?
, what is the perimeter of the triangle?

An acute Isosceles triangle has two sides with length 




In order to solve this problem, first find the length of the missing sides. Then apply the formula: 
The missing side equals:


Then, apply the perimeter formula by plugging in the side values:

In order to solve this problem, first find the length of the missing sides. Then apply the formula:
The missing side equals:
Then, apply the perimeter formula by plugging in the side values:
Compare your answer with the correct one above

The obtuse Isosceles triangle shown above has two sides with length  and one side length
and one side length  . The length of side
. The length of side 
 inches. Side length
inches. Side length  . Find the perimeter of the triangle.
. Find the perimeter of the triangle.

The obtuse Isosceles triangle shown above has two sides with length 




To find the perimeter of this triangle, apply the perimeter formula:

Since,  , and
, and  then
then  must have a value of:
must have a value of: 
This triangle has two side lengths of  inches, and one side length of
inches, and one side length of  inches.
inches.
Thus, the solution is:

To find the perimeter of this triangle, apply the perimeter formula:
Since, 


This triangle has two side lengths of 

Thus, the solution is:
Compare your answer with the correct one above