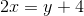Functions and Graphs

Help Questions

GRE Quantitative Reasoning › Functions and Graphs

Questions 1 - 10

At what point does the line cross the y-axis?

Explanation

Step 1: Rearrange the terms into the form y=mx+b. Move the to the other side.

Step 2: Move the 4 to the other side.

Step 3: When the line crosses the y-axis, the x value is zero. We will plug in for x and find the y value.

$\rightarrow y=-4$

So, the point where this line crosses the y-axis is

At what point does the line cross the y-axis?

Explanation

Step 1: Rearrange the terms into the form y=mx+b. Move the to the other side.

Step 2: Move the 4 to the other side.

Step 3: When the line crosses the y-axis, the x value is zero. We will plug in for x and find the y value.

$\rightarrow y=-4$

So, the point where this line crosses the y-axis is

Using the information below, determine the equation of the hyperbola.

Foci: and

Eccentricity:

$\small \small \small \small \small \small \frac{(x-5)^{2}}{4} - \frac{(y-8)^{2}}{12}=1$

$\small \small \small \small \small \small \small \frac{(x-8)^{2}}{4} - \frac{(y-5)^{2}}{12}=1$

$\small \small \small \small \small \small \small \frac{(x-5)^{2}}{12} - \frac{(y-8)^{2}}{4}=1$

$\small \small \small \small \small \small \small \frac{(x-5)^{2}}{4} - \frac{(y-8)^{2}}{16}=1$

$\small \small \small \small \small \small \small \small \frac{(x-8)^{2}}{12} - \frac{(y-5)^{2}}{16}=1$

Explanation

General Information for Hyperbola:

Equation for horizontal transverse hyperbola:

$\small \frac{(x-h)^{2}}{a^{2}} - \frac{(y-k)^{2}}{b^{2}}=1$

Distance between foci =

Distance between vertices =

Eccentricity =

$\small a^{2}+b^{2}=c^{2}$

Center: (h, k)

First determine the value of c. Since we know the distance between the two foci is 8, we can set that equal to .

$\small 8=2c$

$\small \small c= 4$

Next, use the eccentricity equation and the value of the eccentricity provided in the question to determine the value of a.

Eccentricity = $\small \small \small \small c/a=2$

$\small \small \frac{c}{a}=\frac{2}{1}=\frac{4}{a}$

$\small \small 4=2a$

$\small \small a=2$

$\small \small \small a^{2}=4$

Determine the value of $\small b^{2}$

$\small a^{2}+b^{2}=c^{2}$

$\small \small \small 2^{2}+b^{2}=4^{2}$

$\small \small \small b^{2}=12$

Determine the center point to identify the values of h and k. Since the y coordinate of the foci are 8, the center point will be on the same line. Hence, $\small \small k = 8$ .

Since center point is equal distance from both foci, and we know that the distance between the foci is 8, we can conclude that $\small \small h=5$

Center point: $\small \small \small (h, k)= (5, 8 )$

Thus, the equation of the hyperbola is:

$\small \small \small \small \small \small \frac{(x-5)^{2}}{4} - \frac{(y-8)^{2}}{12}=1$

Using the information below, determine the equation of the hyperbola.

Foci: and

Eccentricity:

$\small \small \small \small \small \small \frac{(x-5)^{2}}{4} - \frac{(y-8)^{2}}{12}=1$

$\small \small \small \small \small \small \small \frac{(x-8)^{2}}{4} - \frac{(y-5)^{2}}{12}=1$

$\small \small \small \small \small \small \small \frac{(x-5)^{2}}{12} - \frac{(y-8)^{2}}{4}=1$

$\small \small \small \small \small \small \small \frac{(x-5)^{2}}{4} - \frac{(y-8)^{2}}{16}=1$

$\small \small \small \small \small \small \small \small \frac{(x-8)^{2}}{12} - \frac{(y-5)^{2}}{16}=1$

Explanation

General Information for Hyperbola:

Equation for horizontal transverse hyperbola:

$\small \frac{(x-h)^{2}}{a^{2}} - \frac{(y-k)^{2}}{b^{2}}=1$

Distance between foci =

Distance between vertices =

Eccentricity =

$\small a^{2}+b^{2}=c^{2}$

Center: (h, k)

First determine the value of c. Since we know the distance between the two foci is 8, we can set that equal to .

$\small 8=2c$

$\small \small c= 4$

Next, use the eccentricity equation and the value of the eccentricity provided in the question to determine the value of a.

Eccentricity = $\small \small \small \small c/a=2$

$\small \small \frac{c}{a}=\frac{2}{1}=\frac{4}{a}$

$\small \small 4=2a$

$\small \small a=2$

$\small \small \small a^{2}=4$

Determine the value of $\small b^{2}$

$\small a^{2}+b^{2}=c^{2}$

$\small \small \small 2^{2}+b^{2}=4^{2}$

$\small \small \small b^{2}=12$

Determine the center point to identify the values of h and k. Since the y coordinate of the foci are 8, the center point will be on the same line. Hence, $\small \small k = 8$ .

Since center point is equal distance from both foci, and we know that the distance between the foci is 8, we can conclude that $\small \small h=5$

Center point: $\small \small \small (h, k)= (5, 8 )$

Thus, the equation of the hyperbola is:

$\small \small \small \small \small \small \frac{(x-5)^{2}}{4} - \frac{(y-8)^{2}}{12}=1$

What is the equation of the line (in slope-intercept form) that goes through the points: and ?

$y=\frac {4}{5}x+\frac {12}{5}$

$y=\frac {4}{5}x-\frac {12}{5}$

$y=-\frac {4}{5}x+\frac {12}{5}$

$y=-\frac {4}{5}x-\frac {12}{5}$

Explanation

Step 1: Find the slope between the two points:

$\frac {y_2-y_1}{x_2-x_1}=\frac {8-4}{7-2}=\frac {4}{5}$

Step 2: Write the slope-intercept form:

$y=\frac {4}{5}x+b$

Step 3. Find b. Plug in (x,y) from one of the points:

$4=\frac {4}{5}(2)+b$

$4=\frac {8}{5}+b$

$4-\frac {8}{5}=b$

$\frac {20-8}{5}=b$

$\frac {12}{5}=b$
Step 4: Write out the full equation:

$y=\frac {4}{5}x+\frac {12}{5}$

Find the distance from point $\left ( 1,-\frac{1}{2}\right )$ to the line .

$\frac{11}{2}$

$\frac{9}{2}$

$-\frac{11}{2}$

$-\frac{9}{2}$

Explanation

Draw a line that connects the point and intersects the line at a perpendicular angle.

The vertical distance from the point $\left ( 1,-\frac{1}{2}\right )$ to the line will be the difference of the 2 y-values.

The distance can never be negative.

$5-\left(-\frac{1}{2}\right) = \frac{10}{2}+\frac{1}{2}=\frac{11}{2}$

What is the slope and y-intercept of this line: ?

$Slope=\frac {3}{4},y-intercept=3$

$Slope=\frac {3}{4},y-intercept=2$

$Slope=\frac {-3}{4},y-intercept=3$

$Slope=\frac {4}{3},y-intercept=3$

Explanation

Step 1: Move the y-term to the other side. We will add 4y.

$\rightarrow 3x=12+4y$

Step 2: Move the constant to the other side. We will subtract 12.

$\rightarrow 3x-12=4y$

Step 3: Divide by the coefficient in front of the y term. In this question, we divide all terms by 4.

$\frac {3x-12}{4}=\frac {4y}{4}\rightarrow\frac {3}{4}x+\frac {-12}{4}=y$

$\rightarrow y=\frac {3}{4}x-3$

Step 4: Identify the slope and the y-intercept. The slope is the number that is in front of the x term, and the y-intercept is the number that comes after the x-term.

In this question, the slope is $\frac {3}{4}$ and the y-intercept is .

Find the slope of a line that passes through and

$m=\frac{1}{2}$

$m=-\frac{1}{2}$

Explanation

The formula for slope is:

$m = \frac{y_{2} - y_{1}}{x_{2} -x_{1}}$

$m = \frac{5-(-1)}{6-3}$

$m = \frac{5+1}{6-3}$

$m = \frac{6}{3}$

What is the slope and y-intercept of this line: ?

$Slope=\frac {3}{4},y-intercept=3$

$Slope=\frac {3}{4},y-intercept=2$

$Slope=\frac {-3}{4},y-intercept=3$

$Slope=\frac {4}{3},y-intercept=3$

Explanation

Step 1: Move the y-term to the other side. We will add 4y.

$\rightarrow 3x=12+4y$

Step 2: Move the constant to the other side. We will subtract 12.

$\rightarrow 3x-12=4y$

Step 3: Divide by the coefficient in front of the y term. In this question, we divide all terms by 4.

$\frac {3x-12}{4}=\frac {4y}{4}\rightarrow\frac {3}{4}x+\frac {-12}{4}=y$

$\rightarrow y=\frac {3}{4}x-3$

Step 4: Identify the slope and the y-intercept. The slope is the number that is in front of the x term, and the y-intercept is the number that comes after the x-term.

In this question, the slope is $\frac {3}{4}$ and the y-intercept is .

What kind of function is this: $f(x)=\sqrt[3] {x-1}$ ?