Electromagnetics, Waves, and Optics - GRE Subject Test: Physics
Card 0 of 56
What is the total resistance of a circuit consisting of three resistors in a parallel configuration? The resistors have the following resistance: 
What is the total resistance of a circuit consisting of three resistors in a parallel configuration? The resistors have the following resistance:
The total resistance of a circuit in parallel is given by the following equation:

Now, we just plug in the values, and solve for the total resistance by inverting!


The total resistance of a circuit in parallel is given by the following equation:
Now, we just plug in the values, and solve for the total resistance by inverting!
Compare your answer with the correct one above
What is the total resistance of a circuit containing four resistors ( ) hooked up in series.
) hooked up in series.
What is the total resistance of a circuit containing four resistors (
For a circuit in series, the total resistance is simply given by the sum of each individual resistor:


For a circuit in series, the total resistance is simply given by the sum of each individual resistor:
Compare your answer with the correct one above
A beam of light, with wavelength  , is normally incident on a transmission diffraction grating. With respect to the incident beam, the first order diffraction maximum occurs at an angle of
, is normally incident on a transmission diffraction grating. With respect to the incident beam, the first order diffraction maximum occurs at an angle of  . What is the number of slits per centimeter on the grating?
. What is the number of slits per centimeter on the grating?
A beam of light, with wavelength 

The equation describing maxima of a diffraction grating is:

Where d is the separation of slits, which can also be expressed as:

Substituting d into the first equation and making the small angle approximation, one can solve for  (lines per length):
(lines per length):
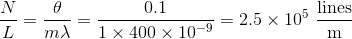
Note that the angle had to be converted from degrees to radians. Finally, the question asks for lines per centimeter, not meter, so the answer becomes  .
.
The equation describing maxima of a diffraction grating is:
Where d is the separation of slits, which can also be expressed as:
Substituting d into the first equation and making the small angle approximation, one can solve for 
Note that the angle had to be converted from degrees to radians. Finally, the question asks for lines per centimeter, not meter, so the answer becomes 
Compare your answer with the correct one above
A car's horn has a frequency of  . As the car drives away from you, you hear the horn at a frequency of
. As the car drives away from you, you hear the horn at a frequency of  . What is the speed of the car?
. What is the speed of the car?

A car's horn has a frequency of 

The equation for the Doppler effect with frequency for a moving source is given by:

Where  is the speed of sound,
is the speed of sound,  is the speed of the source,
is the speed of the source,  is the stationary frequency and
is the stationary frequency and  is the Doppler frequency. Substituting the known values and solving gives us the speed of the car.
is the Doppler frequency. Substituting the known values and solving gives us the speed of the car.

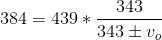

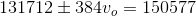

The equation for the Doppler effect with frequency for a moving source is given by:
Where 



Compare your answer with the correct one above
A particle traveling through glass (index of refraction 1.33) emits Cherenkov radiation. Which of the following is a possible speed of the particle?
A particle traveling through glass (index of refraction 1.33) emits Cherenkov radiation. Which of the following is a possible speed of the particle?
Cherenkov radiation is emitted by a particle traveling faster than the phase velocity of light in that medium. Because  , the phase velocity of light in the glass is:
, the phase velocity of light in the glass is:

This is the minimum velocity of a particle to be emitting Cherenkov radiation in glass. This eliminates all answers except  and
and  . The latter is impossible because it is greater than the speed of light in a vacuum, therefore the answer is
. The latter is impossible because it is greater than the speed of light in a vacuum, therefore the answer is  .
.
Cherenkov radiation is emitted by a particle traveling faster than the phase velocity of light in that medium. Because 
This is the minimum velocity of a particle to be emitting Cherenkov radiation in glass. This eliminates all answers except 


Compare your answer with the correct one above
A monochromatic beam of  light travels through a material with a phase velocity of
light travels through a material with a phase velocity of  . What is the refractive index of the material?
. What is the refractive index of the material?
A monochromatic beam of 

The phase velocity of light through a medium with refractive index  is given by:
is given by:

Solving this for  and substituting our given value of
and substituting our given value of  :
:
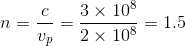
The phase velocity of light through a medium with refractive index 
Solving this for 

Compare your answer with the correct one above
A double slit experiment is set up with the following parameters: two slits are a separated by a distance  . A beam of light with wavelength
. A beam of light with wavelength  shines through the two slits, and is projected onto a screen a distance
shines through the two slits, and is projected onto a screen a distance  from the slits. What is the distance on the screen between the central band and the next band on either side? (This distance is marked '
from the slits. What is the distance on the screen between the central band and the next band on either side? (This distance is marked ' ' on the figure).
' on the figure).

A double slit experiment is set up with the following parameters: two slits are a separated by a distance 




The condition for constructive interference with double slit diffraction is given by:

Where  is 0, 1, 2, ...
is 0, 1, 2, ...
Solving for the angle and using the small angle approximation, we get;
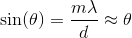
The distance  in the diagram can be related to the other quantities by simple geometry:
in the diagram can be related to the other quantities by simple geometry:
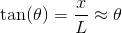
Again, with the help of the small angle approximation. Setting the two thetas equal to each other and solving for  , we get:
, we get:

For the central band,  , so the
, so the  position is also zero. The next band,
position is also zero. The next band,  , yields a distance of:
, yields a distance of:
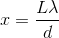
The condition for constructive interference with double slit diffraction is given by:
Where 
Solving for the angle and using the small angle approximation, we get;
The distance 
Again, with the help of the small angle approximation. Setting the two thetas equal to each other and solving for 
For the central band, 


Compare your answer with the correct one above
Two waves with frequencies:  are combined. What is the frequency of the resulting beat?
are combined. What is the frequency of the resulting beat?
Two waves with frequencies: 
The beat from two combined sound waves is:


The beat from two combined sound waves is:
Compare your answer with the correct one above
The focal length of a thin convex lens is  . A candle is placed
. A candle is placed  to the left of the lens. Approximately where is the image of the candle?
to the left of the lens. Approximately where is the image of the candle?
The focal length of a thin convex lens is 

Because the object is beyond 2 focal lengths of the lens, the image must be between 1 and 2 focal lengths on the opposite side. Therefore, the image must be between  on the right side of the lens.
on the right side of the lens.
Alternatively, one can apply the thin lens equation:

Where  is the object distance
is the object distance  and
and  is the focal length
is the focal length  . Plug in these values and solve.
. Plug in these values and solve.



Because the object is beyond 2 focal lengths of the lens, the image must be between 1 and 2 focal lengths on the opposite side. Therefore, the image must be between 
Alternatively, one can apply the thin lens equation:
Where 



Compare your answer with the correct one above
A candle  tall is placed
tall is placed  to the left of a thin convex lens with focal length
to the left of a thin convex lens with focal length  . What is the height and orientation of the image created?
. What is the height and orientation of the image created?
A candle 


First, find the image distance  from the thin lens equation:
from the thin lens equation:




Magnification of a lens is given by:

Where  and
and  are the image height and object height, respectively. The given object height is
are the image height and object height, respectively. The given object height is  , which we can use to solve for the image height:
, which we can use to solve for the image height:

Because the sign is negative, the image is inverted.
First, find the image distance 
Magnification of a lens is given by:
Where 


Because the sign is negative, the image is inverted.
Compare your answer with the correct one above
Sirius is a binary star system, consisting of two white dwarfs with an angular separation of 3 arcseconds. What is the approximate minimum diameter lens needed to resolve the two stars in Sirius for an observation at  ?
?
Sirius is a binary star system, consisting of two white dwarfs with an angular separation of 3 arcseconds. What is the approximate minimum diameter lens needed to resolve the two stars in Sirius for an observation at 
The Rayleigh Criterion gives the diffraction limit on resolution of a particular lens at a particular wavelength:

Where theta is the angular resolution in radians,  is the wavelength of light, and
is the wavelength of light, and  is the diameter the lens in question. Solving for
is the diameter the lens in question. Solving for  and converting 3 arcseconds into radians, one can approximate the diameter to be about
and converting 3 arcseconds into radians, one can approximate the diameter to be about  :
:



The Rayleigh Criterion gives the diffraction limit on resolution of a particular lens at a particular wavelength:
Where theta is the angular resolution in radians, 



Compare your answer with the correct one above
A reflective sphere has a diameter of  . The surface of the sphere makes a convex spherical mirror; what is its focal point?
. The surface of the sphere makes a convex spherical mirror; what is its focal point?
A reflective sphere has a diameter of 
The focal length of a spherical mirror is one half of the radius, which is one quarter of the diameter. In the case of convex mirrors, the focal point is considered behind the surface, which gives the answer its negative sign.
The focal length of a spherical mirror is one half of the radius, which is one quarter of the diameter. In the case of convex mirrors, the focal point is considered behind the surface, which gives the answer its negative sign.
Compare your answer with the correct one above
A beam of unpolarized light passes through two linear polarizers whose polarization axes are at an angle theta with each other. The light initially has an intensity  , and has an intensity of
, and has an intensity of  after passing through both polarizes. Find
after passing through both polarizes. Find  ?
?
A beam of unpolarized light passes through two linear polarizers whose polarization axes are at an angle theta with each other. The light initially has an intensity 


Initially unpolarized light passing though a linear polarizer decreases in intensity by a factor of two:

Malus's Law gives the change in intensity of polarized light passing through a linear polarizer in terms of the change in angle of polarization:

Combining the two equations, we get:

Solving for  :
:

Initially unpolarized light passing though a linear polarizer decreases in intensity by a factor of two:
Malus's Law gives the change in intensity of polarized light passing through a linear polarizer in terms of the change in angle of polarization:
Combining the two equations, we get:
Solving for 
Compare your answer with the correct one above
A beam of light travels through a medium with index of refraction  until it reaches an interface with another material, with index of refraction
until it reaches an interface with another material, with index of refraction 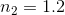 . No light is transmitted into the second material. At what angle (measured from the plane of the interface between the two materials) does the beam hit the second material?
. No light is transmitted into the second material. At what angle (measured from the plane of the interface between the two materials) does the beam hit the second material?
A beam of light travels through a medium with index of refraction 
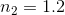
Total internal reflection occurs at the angle:

However, this angle is measured from a line normal to the plane of the interface; the angle we want, therefore, is  , which is
, which is  .
.
Total internal reflection occurs at the angle:
However, this angle is measured from a line normal to the plane of the interface; the angle we want, therefore, is 

Compare your answer with the correct one above
A beam of light, with wavelength  , is normally incident on a transmission diffraction grating. With respect to the incident beam, the first order diffraction maximum occurs at an angle of
, is normally incident on a transmission diffraction grating. With respect to the incident beam, the first order diffraction maximum occurs at an angle of  . What is the number of slits per centimeter on the grating?
. What is the number of slits per centimeter on the grating?
A beam of light, with wavelength 

The equation describing maxima of a diffraction grating is:

Where d is the separation of slits, which can also be expressed as:

Substituting d into the first equation and making the small angle approximation, one can solve for  (lines per length):
(lines per length):
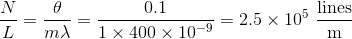
Note that the angle had to be converted from degrees to radians. Finally, the question asks for lines per centimeter, not meter, so the answer becomes  .
.
The equation describing maxima of a diffraction grating is:
Where d is the separation of slits, which can also be expressed as:
Substituting d into the first equation and making the small angle approximation, one can solve for 
Note that the angle had to be converted from degrees to radians. Finally, the question asks for lines per centimeter, not meter, so the answer becomes 
Compare your answer with the correct one above
What is the total resistance of a circuit consisting of three resistors in a parallel configuration? The resistors have the following resistance: 
What is the total resistance of a circuit consisting of three resistors in a parallel configuration? The resistors have the following resistance:
The total resistance of a circuit in parallel is given by the following equation:

Now, we just plug in the values, and solve for the total resistance by inverting!


The total resistance of a circuit in parallel is given by the following equation:
Now, we just plug in the values, and solve for the total resistance by inverting!
Compare your answer with the correct one above
What is the total resistance of a circuit containing four resistors ( ) hooked up in series.
) hooked up in series.
What is the total resistance of a circuit containing four resistors (
For a circuit in series, the total resistance is simply given by the sum of each individual resistor:


For a circuit in series, the total resistance is simply given by the sum of each individual resistor:
Compare your answer with the correct one above
A car's horn has a frequency of  . As the car drives away from you, you hear the horn at a frequency of
. As the car drives away from you, you hear the horn at a frequency of  . What is the speed of the car?
. What is the speed of the car?

A car's horn has a frequency of 

The equation for the Doppler effect with frequency for a moving source is given by:

Where  is the speed of sound,
is the speed of sound,  is the speed of the source,
is the speed of the source,  is the stationary frequency and
is the stationary frequency and  is the Doppler frequency. Substituting the known values and solving gives us the speed of the car.
is the Doppler frequency. Substituting the known values and solving gives us the speed of the car.

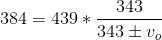

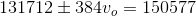

The equation for the Doppler effect with frequency for a moving source is given by:
Where 



Compare your answer with the correct one above
A particle traveling through glass (index of refraction 1.33) emits Cherenkov radiation. Which of the following is a possible speed of the particle?
A particle traveling through glass (index of refraction 1.33) emits Cherenkov radiation. Which of the following is a possible speed of the particle?
Cherenkov radiation is emitted by a particle traveling faster than the phase velocity of light in that medium. Because  , the phase velocity of light in the glass is:
, the phase velocity of light in the glass is:

This is the minimum velocity of a particle to be emitting Cherenkov radiation in glass. This eliminates all answers except  and
and  . The latter is impossible because it is greater than the speed of light in a vacuum, therefore the answer is
. The latter is impossible because it is greater than the speed of light in a vacuum, therefore the answer is  .
.
Cherenkov radiation is emitted by a particle traveling faster than the phase velocity of light in that medium. Because 
This is the minimum velocity of a particle to be emitting Cherenkov radiation in glass. This eliminates all answers except 


Compare your answer with the correct one above
A monochromatic beam of  light travels through a material with a phase velocity of
light travels through a material with a phase velocity of  . What is the refractive index of the material?
. What is the refractive index of the material?
A monochromatic beam of 

The phase velocity of light through a medium with refractive index  is given by:
is given by:

Solving this for  and substituting our given value of
and substituting our given value of  :
:
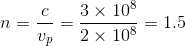
The phase velocity of light through a medium with refractive index 
Solving this for 

Compare your answer with the correct one above