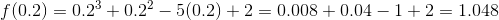Identification - HiSET
Card 0 of 8
The equation

has two distinct solutions. What is their sum?
The equation
has two distinct solutions. What is their sum?
Tap to see back →
It is not necessary to actually find the solutions to a quadratic equation to determine the sum of its solutions.
First, get the equation in standard form  by subtracting
by subtracting  from both sides:
from both sides:



If a quadratic equation has two distinct solutions, which we are given here, their sum is the linear coefficient  . In this problem,
. In this problem,  , making
, making  the correct choice.
the correct choice.
It is not necessary to actually find the solutions to a quadratic equation to determine the sum of its solutions.
First, get the equation in standard form 

If a quadratic equation has two distinct solutions, which we are given here, their sum is the linear coefficient 


The equation

has two distinct solutions. What is their sum?
The equation
has two distinct solutions. What is their sum?
Tap to see back →
It is not necessary to actually find the solutions to a quadratic equation to determine the sum of its solutions.
First, get the equation in standard form  by subtracting
by subtracting  from both sides:
from both sides:



If a quadratic equation has two distinct solutions, which we are given here, their sum is the linear coefficient  . In this problem,
. In this problem,  , making
, making  the correct choice.
the correct choice.
It is not necessary to actually find the solutions to a quadratic equation to determine the sum of its solutions.
First, get the equation in standard form 

If a quadratic equation has two distinct solutions, which we are given here, their sum is the linear coefficient 


The equation

has two distinct solutions. What is their sum?
The equation
has two distinct solutions. What is their sum?
Tap to see back →
It is not necessary to actually find the solutions to a quadratic equation to determine the sum of its solutions.
First, get the equation in standard form  by subtracting
by subtracting  from both sides:
from both sides:



If a quadratic equation has two distinct solutions, which we are given here, their sum is the linear coefficient  . In this problem,
. In this problem,  , making
, making  the correct choice.
the correct choice.
It is not necessary to actually find the solutions to a quadratic equation to determine the sum of its solutions.
First, get the equation in standard form 

If a quadratic equation has two distinct solutions, which we are given here, their sum is the linear coefficient 


The equation

has two distinct solutions. What is their sum?
The equation
has two distinct solutions. What is their sum?
Tap to see back →
It is not necessary to actually find the solutions to a quadratic equation to determine the sum of its solutions.
First, get the equation in standard form  by subtracting
by subtracting  from both sides:
from both sides:



If a quadratic equation has two distinct solutions, which we are given here, their sum is the linear coefficient  . In this problem,
. In this problem,  , making
, making  the correct choice.
the correct choice.
It is not necessary to actually find the solutions to a quadratic equation to determine the sum of its solutions.
First, get the equation in standard form 

If a quadratic equation has two distinct solutions, which we are given here, their sum is the linear coefficient 


The graph of the polynomial function

has one and only one zero on the interval  . On which subinterval is it located?
. On which subinterval is it located?
The graph of the polynomial function
has one and only one zero on the interval 
Tap to see back →
The Intermediate Value Theorem (IVT) states that if the graph of a function  is continuous on an interval
is continuous on an interval ![[a, b]](//cdn-s3.varsitytutors.com/uploads/formula_image/image/1094264/gif.latex) , and
, and  and
and  differ in sign, then
differ in sign, then  has a zero on
has a zero on  . Consequently, the way to answer this question is to determine the signs of
. Consequently, the way to answer this question is to determine the signs of  on the endpoints of the subintervals -
on the endpoints of the subintervals -  . We can do this by substituting each value for
. We can do this by substituting each value for  as follows:
as follows:


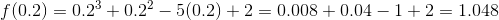




 assumes positive values for
assumes positive values for  and negative values for
and negative values for  . By the IVT,
. By the IVT,  has a zero on
has a zero on  .
.
The Intermediate Value Theorem (IVT) states that if the graph of a function 
![[a, b]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1094264/gif.latex)












The graph of the polynomial function

has one and only one zero on the interval  . On which subinterval is it located?
. On which subinterval is it located?
The graph of the polynomial function
has one and only one zero on the interval 
Tap to see back →
The Intermediate Value Theorem (IVT) states that if the graph of a function  is continuous on an interval
is continuous on an interval ![[a, b]](//cdn-s3.varsitytutors.com/uploads/formula_image/image/1094264/gif.latex) , and
, and  and
and  differ in sign, then
differ in sign, then  has a zero on
has a zero on  . Consequently, the way to answer this question is to determine the signs of
. Consequently, the way to answer this question is to determine the signs of  on the endpoints of the subintervals -
on the endpoints of the subintervals -  . We can do this by substituting each value for
. We can do this by substituting each value for  as follows:
as follows:


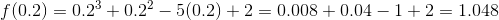




 assumes positive values for
assumes positive values for  and negative values for
and negative values for  . By the IVT,
. By the IVT,  has a zero on
has a zero on  .
.
The Intermediate Value Theorem (IVT) states that if the graph of a function 
![[a, b]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1094264/gif.latex)












The graph of the polynomial function

has one and only one zero on the interval  . On which subinterval is it located?
. On which subinterval is it located?
The graph of the polynomial function
has one and only one zero on the interval 
Tap to see back →
The Intermediate Value Theorem (IVT) states that if the graph of a function  is continuous on an interval
is continuous on an interval ![[a, b]](//cdn-s3.varsitytutors.com/uploads/formula_image/image/1094264/gif.latex) , and
, and  and
and  differ in sign, then
differ in sign, then  has a zero on
has a zero on  . Consequently, the way to answer this question is to determine the signs of
. Consequently, the way to answer this question is to determine the signs of  on the endpoints of the subintervals -
on the endpoints of the subintervals -  . We can do this by substituting each value for
. We can do this by substituting each value for  as follows:
as follows:


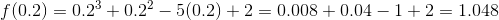




 assumes positive values for
assumes positive values for  and negative values for
and negative values for  . By the IVT,
. By the IVT,  has a zero on
has a zero on  .
.
The Intermediate Value Theorem (IVT) states that if the graph of a function 
![[a, b]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1094264/gif.latex)












The graph of the polynomial function

has one and only one zero on the interval  . On which subinterval is it located?
. On which subinterval is it located?
The graph of the polynomial function
has one and only one zero on the interval 
Tap to see back →
The Intermediate Value Theorem (IVT) states that if the graph of a function  is continuous on an interval
is continuous on an interval ![[a, b]](//cdn-s3.varsitytutors.com/uploads/formula_image/image/1094264/gif.latex) , and
, and  and
and  differ in sign, then
differ in sign, then  has a zero on
has a zero on  . Consequently, the way to answer this question is to determine the signs of
. Consequently, the way to answer this question is to determine the signs of  on the endpoints of the subintervals -
on the endpoints of the subintervals -  . We can do this by substituting each value for
. We can do this by substituting each value for  as follows:
as follows:


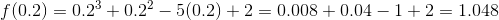




 assumes positive values for
assumes positive values for  and negative values for
and negative values for  . By the IVT,
. By the IVT,  has a zero on
has a zero on  .
.
The Intermediate Value Theorem (IVT) states that if the graph of a function 
![[a, b]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1094264/gif.latex)