Rhombuses - ISEE Upper Level Quantitative Reasoning
Card 0 of 36
Consider the rhombus below. Solve for 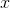 .
.

Consider the rhombus below. Solve for 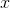

The total sum of the interior angles of a quadrilateral is  degrees. In this problem, we are only considering half of the interior angles:
degrees. In this problem, we are only considering half of the interior angles:



The total sum of the interior angles of a quadrilateral is 
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
The above depicts a rhombus and one of its diagonals. What is 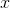 ?
?

Note: Figure NOT drawn to scale.
The above depicts a rhombus and one of its diagonals. What is 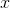
The diagonals of a rhombus bisect the angles.
The angle bisected must be supplementary to the  angle since they are consecutive angles of a parallelogram; therefore, that angle has measure
angle since they are consecutive angles of a parallelogram; therefore, that angle has measure 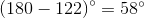 , and
, and  is half that, or
is half that, or 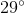 .
.
The diagonals of a rhombus bisect the angles.
The angle bisected must be supplementary to the 
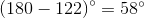

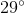
Compare your answer with the correct one above
Two diagonals of a rhombus have lengths of  and
and  . Give the area in terms of
. Give the area in terms of  .
.
Two diagonals of a rhombus have lengths of 


The formula for the area of a rhombus is
 ,
,
where  is the length of one diagonal and
is the length of one diagonal and  is the length of the other diagonal.
is the length of the other diagonal.

The formula for the area of a rhombus is

where 

Compare your answer with the correct one above
A rhombus has side length  , and one of the interior angles is
, and one of the interior angles is  . Give the area of the rhombus.
. Give the area of the rhombus.
A rhombus has side length 

The area of a rhombus can be determined by the following formula:
 ,
,
where  is the length of any side and
is the length of any side and  is any interior angle.
is any interior angle.

The area of a rhombus can be determined by the following formula:

where 

Compare your answer with the correct one above
Find the area of a rhombus with one diagonal having a length of 12in and the other having a length two times the first diagonal.
Find the area of a rhombus with one diagonal having a length of 12in and the other having a length two times the first diagonal.
To find the area of a rhombus, we will use the following formula:

where p and q are the lengths of the diagonals of the rhombus.
Now, we know one diagonal has a length of 12in. We also know the other diagonal is two times the first diagonal. Therefore, the second diagonal is 24in.
Knowing this, we can substitute into the formula. We get



To find the area of a rhombus, we will use the following formula:
where p and q are the lengths of the diagonals of the rhombus.
Now, we know one diagonal has a length of 12in. We also know the other diagonal is two times the first diagonal. Therefore, the second diagonal is 24in.
Knowing this, we can substitute into the formula. We get
Compare your answer with the correct one above
A rhombus has a perimeter of  . Give the side length of the rhombus.
. Give the side length of the rhombus.
A rhombus has a perimeter of 
Like any polygon, the perimeter of the rhombus is the total distance around the outside, which can be found by adding together the length of each side. In the case of a rhombus, all four sides have the same length, i.e.
 ,
,
where  is the length of each side.
is the length of each side.

Like any polygon, the perimeter of the rhombus is the total distance around the outside, which can be found by adding together the length of each side. In the case of a rhombus, all four sides have the same length, i.e.

where 
Compare your answer with the correct one above
A rhombus has the area of  . One of the interior angles is
. One of the interior angles is  . Give the length of each side of the rhombus.
. Give the length of each side of the rhombus.
A rhombus has the area of 

The area of a rhombus can be determined by the following formula:
 ,
,
where  is the length of any side and
is the length of any side and  is any interior angle.
is any interior angle.


The area of a rhombus can be determined by the following formula:

where 

Compare your answer with the correct one above
One side of a rhombus measures 2 yards. Which of the following is equal to the perimeter?
One side of a rhombus measures 2 yards. Which of the following is equal to the perimeter?
A rhombus has four sides of equal measure, so the perimeter of a rhombus with sidelength 2 yards is  yards.
yards.

Also,

The only choice that agrees with any of these measures is 288 inches, the correct choice.
A rhombus has four sides of equal measure, so the perimeter of a rhombus with sidelength 2 yards is 
Also,
The only choice that agrees with any of these measures is 288 inches, the correct choice.
Compare your answer with the correct one above
One side of a rhombus measures  . Give its perimeter in terms of
. Give its perimeter in terms of  .
.
One side of a rhombus measures 

A rhombus has four sides of equal measure, so the perimeter of a rhombus with sidelength  is
is  .
.
A rhombus has four sides of equal measure, so the perimeter of a rhombus with sidelength 

Compare your answer with the correct one above
Consider the rhombus below. Solve for 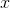 .
.

Consider the rhombus below. Solve for 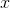

The total sum of the interior angles of a quadrilateral is  degrees. In this problem, we are only considering half of the interior angles:
degrees. In this problem, we are only considering half of the interior angles:



The total sum of the interior angles of a quadrilateral is 
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
The above depicts a rhombus and one of its diagonals. What is 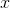 ?
?

Note: Figure NOT drawn to scale.
The above depicts a rhombus and one of its diagonals. What is 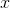
The diagonals of a rhombus bisect the angles.
The angle bisected must be supplementary to the  angle since they are consecutive angles of a parallelogram; therefore, that angle has measure
angle since they are consecutive angles of a parallelogram; therefore, that angle has measure 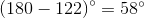 , and
, and  is half that, or
is half that, or 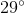 .
.
The diagonals of a rhombus bisect the angles.
The angle bisected must be supplementary to the 

Compare your answer with the correct one above
Two diagonals of a rhombus have lengths of  and
and  . Give the area in terms of
. Give the area in terms of  .
.
Two diagonals of a rhombus have lengths of 


The formula for the area of a rhombus is
 ,
,
where  is the length of one diagonal and
is the length of one diagonal and  is the length of the other diagonal.
is the length of the other diagonal.

The formula for the area of a rhombus is

where 

Compare your answer with the correct one above
A rhombus has side length  , and one of the interior angles is
, and one of the interior angles is  . Give the area of the rhombus.
. Give the area of the rhombus.
A rhombus has side length 

The area of a rhombus can be determined by the following formula:
 ,
,
where  is the length of any side and
is the length of any side and  is any interior angle.
is any interior angle.

The area of a rhombus can be determined by the following formula:

where 

Compare your answer with the correct one above
Find the area of a rhombus with one diagonal having a length of 12in and the other having a length two times the first diagonal.
Find the area of a rhombus with one diagonal having a length of 12in and the other having a length two times the first diagonal.
To find the area of a rhombus, we will use the following formula:

where p and q are the lengths of the diagonals of the rhombus.
Now, we know one diagonal has a length of 12in. We also know the other diagonal is two times the first diagonal. Therefore, the second diagonal is 24in.
Knowing this, we can substitute into the formula. We get



To find the area of a rhombus, we will use the following formula:
where p and q are the lengths of the diagonals of the rhombus.
Now, we know one diagonal has a length of 12in. We also know the other diagonal is two times the first diagonal. Therefore, the second diagonal is 24in.
Knowing this, we can substitute into the formula. We get
Compare your answer with the correct one above
A rhombus has a perimeter of  . Give the side length of the rhombus.
. Give the side length of the rhombus.
A rhombus has a perimeter of 
Like any polygon, the perimeter of the rhombus is the total distance around the outside, which can be found by adding together the length of each side. In the case of a rhombus, all four sides have the same length, i.e.
 ,
,
where  is the length of each side.
is the length of each side.

Like any polygon, the perimeter of the rhombus is the total distance around the outside, which can be found by adding together the length of each side. In the case of a rhombus, all four sides have the same length, i.e.

where 
Compare your answer with the correct one above
A rhombus has the area of  . One of the interior angles is
. One of the interior angles is  . Give the length of each side of the rhombus.
. Give the length of each side of the rhombus.
A rhombus has the area of 

The area of a rhombus can be determined by the following formula:
 ,
,
where  is the length of any side and
is the length of any side and  is any interior angle.
is any interior angle.


The area of a rhombus can be determined by the following formula:

where 

Compare your answer with the correct one above
One side of a rhombus measures 2 yards. Which of the following is equal to the perimeter?
One side of a rhombus measures 2 yards. Which of the following is equal to the perimeter?
A rhombus has four sides of equal measure, so the perimeter of a rhombus with sidelength 2 yards is  yards.
yards.

Also,

The only choice that agrees with any of these measures is 288 inches, the correct choice.
A rhombus has four sides of equal measure, so the perimeter of a rhombus with sidelength 2 yards is 
Also,
The only choice that agrees with any of these measures is 288 inches, the correct choice.
Compare your answer with the correct one above
One side of a rhombus measures  . Give its perimeter in terms of
. Give its perimeter in terms of  .
.
One side of a rhombus measures 

A rhombus has four sides of equal measure, so the perimeter of a rhombus with sidelength  is
is  .
.
A rhombus has four sides of equal measure, so the perimeter of a rhombus with sidelength 

Compare your answer with the correct one above
Consider the rhombus below. Solve for 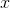 .
.

Consider the rhombus below. Solve for 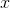

The total sum of the interior angles of a quadrilateral is  degrees. In this problem, we are only considering half of the interior angles:
degrees. In this problem, we are only considering half of the interior angles:



The total sum of the interior angles of a quadrilateral is 
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
The above depicts a rhombus and one of its diagonals. What is 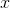 ?
?

Note: Figure NOT drawn to scale.
The above depicts a rhombus and one of its diagonals. What is 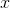
The diagonals of a rhombus bisect the angles.
The angle bisected must be supplementary to the  angle since they are consecutive angles of a parallelogram; therefore, that angle has measure
angle since they are consecutive angles of a parallelogram; therefore, that angle has measure 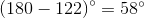 , and
, and  is half that, or
is half that, or 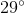 .
.
The diagonals of a rhombus bisect the angles.
The angle bisected must be supplementary to the 

Compare your answer with the correct one above