Series in Calculus - Math
Card 0 of 20
Give the  term of the Taylor series expansion of the function
term of the Taylor series expansion of the function  about
about  .
.
Give the 


The  term of a Taylor series expansion about
term of a Taylor series expansion about  is
is
 .
.
We can find  by differentiating twice in succession:
by differentiating twice in succession:








so the  term is
term is 
The 


We can find 
so the 
Compare your answer with the correct one above
Give the  term of the Maclaurin series expansion of the function
term of the Maclaurin series expansion of the function  .
.
Give the 

The  term of a Maclaurin series expansion has coefficient
term of a Maclaurin series expansion has coefficient
 .
.
We can find  by differentiating twice in succession:
by differentiating twice in succession:




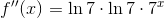


The coefficient we want is
 ,
,
so the corresponding term is  .
.
The 

We can find 
The coefficient we want is

so the corresponding term is 
Compare your answer with the correct one above
Give the  term of the Maclaurin series expansion of the function
term of the Maclaurin series expansion of the function  .
.
Give the 

This can most easily be answered by recalling that the Maclaurin series for  is
is

Multiply by  to get:
to get:


The  term is therefore
term is therefore  .
.
This can most easily be answered by recalling that the Maclaurin series for 
Multiply by 
The 

Compare your answer with the correct one above
Give the  term of the Maclaurin series of the function
term of the Maclaurin series of the function  .
.
Give the 

The  term of a Maclaurin series expansion has coefficient
term of a Maclaurin series expansion has coefficient
 .
.
We can find  by differentiating three times in succession:
by differentiating three times in succession:





The term we want is therefore

The 

We can find 
The term we want is therefore
Compare your answer with the correct one above
Give the  term of the Maclaurin series of the function
term of the Maclaurin series of the function 
Give the 
The  term of the Maclaurin series of a function
term of the Maclaurin series of a function  has coefficient
has coefficient 
The second derivative of  can be found as follows:
can be found as follows:




The coeficient of  in the Maclaurin series is therefore
in the Maclaurin series is therefore

The 

The second derivative of 
The coeficient of 
Compare your answer with the correct one above
Give the  term of the Taylor series expansion of the function
term of the Taylor series expansion of the function  about
about  .
.
Give the 


The  term of a Taylor series expansion about
term of a Taylor series expansion about  is
is
 .
.
We can find  by differentiating twice in succession:
by differentiating twice in succession:








so the  term is
term is 
The 


We can find 
so the 
Compare your answer with the correct one above
Give the  term of the Maclaurin series expansion of the function
term of the Maclaurin series expansion of the function  .
.
Give the 

The  term of a Maclaurin series expansion has coefficient
term of a Maclaurin series expansion has coefficient
 .
.
We can find  by differentiating twice in succession:
by differentiating twice in succession:




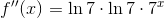


The coefficient we want is
 ,
,
so the corresponding term is  .
.
The 

We can find 
The coefficient we want is

so the corresponding term is 
Compare your answer with the correct one above
Give the  term of the Maclaurin series expansion of the function
term of the Maclaurin series expansion of the function  .
.
Give the 

This can most easily be answered by recalling that the Maclaurin series for  is
is

Multiply by  to get:
to get:


The  term is therefore
term is therefore  .
.
This can most easily be answered by recalling that the Maclaurin series for 
Multiply by 
The 

Compare your answer with the correct one above
Give the  term of the Maclaurin series of the function
term of the Maclaurin series of the function  .
.
Give the 

The  term of a Maclaurin series expansion has coefficient
term of a Maclaurin series expansion has coefficient
 .
.
We can find  by differentiating three times in succession:
by differentiating three times in succession:





The term we want is therefore

The 

We can find 
The term we want is therefore
Compare your answer with the correct one above
Give the  term of the Maclaurin series of the function
term of the Maclaurin series of the function 
Give the 
The  term of the Maclaurin series of a function
term of the Maclaurin series of a function  has coefficient
has coefficient 
The second derivative of  can be found as follows:
can be found as follows:




The coeficient of  in the Maclaurin series is therefore
in the Maclaurin series is therefore

The 

The second derivative of 
The coeficient of 
Compare your answer with the correct one above
Give the  term of the Maclaurin series expansion of the function
term of the Maclaurin series expansion of the function  .
.
Give the 

The  term of a Maclaurin series expansion has coefficient
term of a Maclaurin series expansion has coefficient
 .
.
We can find  by differentiating twice in succession:
by differentiating twice in succession:




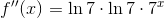


The coefficient we want is
 ,
,
so the corresponding term is  .
.
The 

We can find 
The coefficient we want is

so the corresponding term is 
Compare your answer with the correct one above
Give the  term of the Maclaurin series expansion of the function
term of the Maclaurin series expansion of the function  .
.
Give the 

This can most easily be answered by recalling that the Maclaurin series for  is
is

Multiply by  to get:
to get:


The  term is therefore
term is therefore  .
.
This can most easily be answered by recalling that the Maclaurin series for 
Multiply by 
The 

Compare your answer with the correct one above
Give the  term of the Maclaurin series of the function
term of the Maclaurin series of the function  .
.
Give the 

The  term of a Maclaurin series expansion has coefficient
term of a Maclaurin series expansion has coefficient
 .
.
We can find  by differentiating three times in succession:
by differentiating three times in succession:





The term we want is therefore

The 

We can find 
The term we want is therefore
Compare your answer with the correct one above
Give the  term of the Maclaurin series of the function
term of the Maclaurin series of the function 
Give the 
The  term of the Maclaurin series of a function
term of the Maclaurin series of a function  has coefficient
has coefficient 
The second derivative of  can be found as follows:
can be found as follows:




The coeficient of  in the Maclaurin series is therefore
in the Maclaurin series is therefore

The 

The second derivative of 
The coeficient of 
Compare your answer with the correct one above
Give the  term of the Taylor series expansion of the function
term of the Taylor series expansion of the function  about
about  .
.
Give the 


The  term of a Taylor series expansion about
term of a Taylor series expansion about  is
is
 .
.
We can find  by differentiating twice in succession:
by differentiating twice in succession:








so the  term is
term is 
The 


We can find 
so the 
Compare your answer with the correct one above
Give the  term of the Maclaurin series expansion of the function
term of the Maclaurin series expansion of the function  .
.
Give the 

The  term of a Maclaurin series expansion has coefficient
term of a Maclaurin series expansion has coefficient
 .
.
We can find  by differentiating twice in succession:
by differentiating twice in succession:




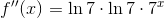


The coefficient we want is
 ,
,
so the corresponding term is  .
.
The 

We can find 
The coefficient we want is

so the corresponding term is 
Compare your answer with the correct one above
Give the  term of the Maclaurin series expansion of the function
term of the Maclaurin series expansion of the function  .
.
Give the 

This can most easily be answered by recalling that the Maclaurin series for  is
is

Multiply by  to get:
to get:


The  term is therefore
term is therefore  .
.
This can most easily be answered by recalling that the Maclaurin series for 
Multiply by 
The 

Compare your answer with the correct one above
Give the  term of the Maclaurin series of the function
term of the Maclaurin series of the function  .
.
Give the 

The  term of a Maclaurin series expansion has coefficient
term of a Maclaurin series expansion has coefficient
 .
.
We can find  by differentiating three times in succession:
by differentiating three times in succession:





The term we want is therefore

The 

We can find 
The term we want is therefore
Compare your answer with the correct one above
Give the  term of the Maclaurin series of the function
term of the Maclaurin series of the function 
Give the 
The  term of the Maclaurin series of a function
term of the Maclaurin series of a function  has coefficient
has coefficient 
The second derivative of  can be found as follows:
can be found as follows:




The coeficient of  in the Maclaurin series is therefore
in the Maclaurin series is therefore

The 

The second derivative of 
The coeficient of 
Compare your answer with the correct one above
Give the  term of the Taylor series expansion of the function
term of the Taylor series expansion of the function  about
about  .
.
Give the 


The  term of a Taylor series expansion about
term of a Taylor series expansion about  is
is
 .
.
We can find  by differentiating twice in succession:
by differentiating twice in succession:








so the  term is
term is 
The 


We can find 
so the 
Compare your answer with the correct one above