Parabolas - Math
Card 0 of 8
What is the minimal value of

over all real numbers?
What is the minimal value of
over all real numbers?
Since this is an upwards-opening parabola, its minimum value will occur at the vertex. The  -coordinate for the vertex of any parabola of the form
-coordinate for the vertex of any parabola of the form

is at
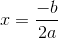
So here,



We plug this value back into the equation of the parabola, to find the value of the function at this 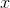 .
.

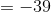
Thus the minimal value of the expression is  .
.
Since this is an upwards-opening parabola, its minimum value will occur at the vertex. The 
is at
So here,
We plug this value back into the equation of the parabola, to find the value of the function at this 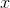
Thus the minimal value of the expression is 
Compare your answer with the correct one above
Find the vertex  for a parabola with equation
for a parabola with equation
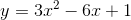
Find the vertex 
For any parabola of the form 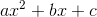 , the
, the 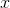 -coordinate of its vertex is
-coordinate of its vertex is
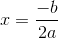
So here, we have

= 
We plug this back into the original equation to find 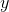 :
:

= 
For any parabola of the form 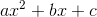
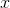
So here, we have
=
We plug this back into the original equation to find 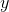
=
Compare your answer with the correct one above
Find the vertex  for a parabola with equation
for a parabola with equation
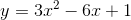
Find the vertex 
For any parabola of the form 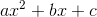 , the
, the 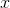 -coordinate of its vertex is
-coordinate of its vertex is
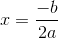
So here, we have

= 
We plug this back into the original equation to find 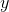 :
:

= 
For any parabola of the form 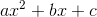
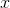
So here, we have
=
We plug this back into the original equation to find 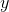
=
Compare your answer with the correct one above
Find the vertex  for a parabola with equation
for a parabola with equation
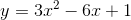
Find the vertex 
For any parabola of the form 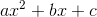 , the
, the 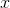 -coordinate of its vertex is
-coordinate of its vertex is
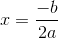
So here, we have

= 
We plug this back into the original equation to find 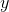 :
:

= 
For any parabola of the form 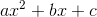
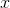
So here, we have
=
We plug this back into the original equation to find 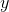
=
Compare your answer with the correct one above
What is the minimal value of

over all real numbers?
What is the minimal value of
over all real numbers?
Since this is an upwards-opening parabola, its minimum value will occur at the vertex. The  -coordinate for the vertex of any parabola of the form
-coordinate for the vertex of any parabola of the form

is at
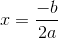
So here,



We plug this value back into the equation of the parabola, to find the value of the function at this 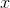 .
.

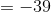
Thus the minimal value of the expression is  .
.
Since this is an upwards-opening parabola, its minimum value will occur at the vertex. The 
is at
So here,
We plug this value back into the equation of the parabola, to find the value of the function at this 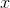
Thus the minimal value of the expression is 
Compare your answer with the correct one above
What is the minimal value of

over all real numbers?
What is the minimal value of
over all real numbers?
Since this is an upwards-opening parabola, its minimum value will occur at the vertex. The  -coordinate for the vertex of any parabola of the form
-coordinate for the vertex of any parabola of the form

is at
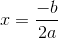
So here,



We plug this value back into the equation of the parabola, to find the value of the function at this 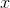 .
.

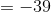
Thus the minimal value of the expression is  .
.
Since this is an upwards-opening parabola, its minimum value will occur at the vertex. The 
is at
So here,
We plug this value back into the equation of the parabola, to find the value of the function at this 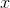
Thus the minimal value of the expression is 
Compare your answer with the correct one above
What is the minimal value of

over all real numbers?
What is the minimal value of
over all real numbers?
Since this is an upwards-opening parabola, its minimum value will occur at the vertex. The  -coordinate for the vertex of any parabola of the form
-coordinate for the vertex of any parabola of the form

is at
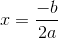
So here,



We plug this value back into the equation of the parabola, to find the value of the function at this 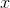 .
.

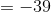
Thus the minimal value of the expression is  .
.
Since this is an upwards-opening parabola, its minimum value will occur at the vertex. The 
is at
So here,
We plug this value back into the equation of the parabola, to find the value of the function at this 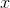
Thus the minimal value of the expression is 
Compare your answer with the correct one above
Find the vertex  for a parabola with equation
for a parabola with equation
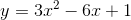
Find the vertex 
For any parabola of the form 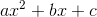 , the
, the 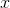 -coordinate of its vertex is
-coordinate of its vertex is
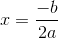
So here, we have

= 
We plug this back into the original equation to find 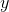 :
:

= 
For any parabola of the form 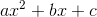
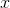
So here, we have
=
We plug this back into the original equation to find 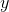
=
Compare your answer with the correct one above