Pentagons - Math
Card 0 of 344
A pentagon with a perimeter of one mile has three congruent sides. The second-longest side is 250 feet longer than any one of those three congruent sides, and the longest side is 500 feet longer than the second-longest side.
Which is the greater quantity?
(a) The length of the longest side of the pentagon
(b) Twice the length of one of the three shortest sides of the pentagon
A pentagon with a perimeter of one mile has three congruent sides. The second-longest side is 250 feet longer than any one of those three congruent sides, and the longest side is 500 feet longer than the second-longest side.
Which is the greater quantity?
(a) The length of the longest side of the pentagon
(b) Twice the length of one of the three shortest sides of the pentagon
If each of the five congruent sides has measure  , then the other two sides have measures
, then the other two sides have measures  and
and  . Add the sides to get the perimeter, which is equal to
. Add the sides to get the perimeter, which is equal to  feet, the solve for
feet, the solve for  :
:





 feet
feet
Now we can compare (a) and (b).
(a) The longest side has measure  feet.
feet.
(b) The three shortest sides each have length 856 feet; twice this is  feet.
feet.
(b) is greater.
If each of the five congruent sides has measure 





Now we can compare (a) and (b).
(a) The longest side has measure 
(b) The three shortest sides each have length 856 feet; twice this is 
(b) is greater.
Compare your answer with the correct one above
A regular pentagon has perimeter one yard. Which is the greater quantity?
(A) The length of one side
(B) 7 inches
A regular pentagon has perimeter one yard. Which is the greater quantity?
(A) The length of one side
(B) 7 inches
One yard is equal to 36 inches. A regular pentagon has five sides of equal length, so one side of the pentagon has length
 inches.
inches.
Since  , (A) is greater.
, (A) is greater.
One yard is equal to 36 inches. A regular pentagon has five sides of equal length, so one side of the pentagon has length

Since 
Compare your answer with the correct one above
A regular pentagon has a side length of  inches and an apothem length of
inches and an apothem length of  inches. Find the area of the pentagon.
inches. Find the area of the pentagon.
A regular pentagon has a side length of 

By definition a regular pentagon must have  equal sides and
equal sides and  equivalent interior angles. Since we are told that this pentagon has a side length of
equivalent interior angles. Since we are told that this pentagon has a side length of  inches, all of the sides must have a length of
inches, all of the sides must have a length of  inches. Additionally, the question provides the length of the apothem of the pentagon--which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into
inches. Additionally, the question provides the length of the apothem of the pentagon--which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into  equivalent interior triangles. Each triangle will have a base of
equivalent interior triangles. Each triangle will have a base of  and a height of
and a height of  .
.
The area of this pentagon can be found by applying the area of a triangle formula:


Note: the area shown above is only the a measurement from one of the five total interior triangles. Thus, to find the total area of the pentagon multiply:

By definition a regular pentagon must have 






The area of this pentagon can be found by applying the area of a triangle formula:
Note: the area shown above is only the a measurement from one of the five total interior triangles. Thus, to find the total area of the pentagon multiply:
Compare your answer with the correct one above
A regular pentagon has an area of  square units and an apothem measurement of
square units and an apothem measurement of  . Find the length of one side of the pentagon.
. Find the length of one side of the pentagon.
A regular pentagon has an area of 

A regular pentagon must have five equivalent sides and five equivalent interior angles. Regular pentagons can be divided up into five equivalent interior triangles, where the base of the triangle is a side length and the height of the triangle is the apothem. This problem provides the total area for the pentagon.
Therefore, you must work backwards using the area formula:  , where the base is equal to the length of one side of the triangle and the height of the triangle is the measurement of the apothem. However, this will only provide the measurement for one of the five interior triangles, thus you first need to divide the total area by
, where the base is equal to the length of one side of the triangle and the height of the triangle is the measurement of the apothem. However, this will only provide the measurement for one of the five interior triangles, thus you first need to divide the total area by 
The solution is:

So, area of one of the five interior triangles is equal to: 
Now, apply the area formula:



A regular pentagon must have five equivalent sides and five equivalent interior angles. Regular pentagons can be divided up into five equivalent interior triangles, where the base of the triangle is a side length and the height of the triangle is the apothem. This problem provides the total area for the pentagon.
Therefore, you must work backwards using the area formula: 
The solution is:
So, area of one of the five interior triangles is equal to:
Now, apply the area formula:
Compare your answer with the correct one above
A regular pentagon has an area of  square units and an apothem measurement of
square units and an apothem measurement of  . Find the length of one side of the pentagon.
. Find the length of one side of the pentagon.
A regular pentagon has an area of 

A regular pentagon must have five equivalent sides and five equivalent interior angles. Regular pentagons can be divided up into five equivalent interior triangles, where the base of the triangle is a side length and the height of the triangle is the apothem. This problem provides the total area for the pentagon.
Therefore, you must work backwards using the area formula:  , where the base is equal to the length of one side of the triangle and the height of the triangle is the measurement of the apothem. However, this will only provide the measurement for one of the five interior triangles, thus you first need to divide the total area by
, where the base is equal to the length of one side of the triangle and the height of the triangle is the measurement of the apothem. However, this will only provide the measurement for one of the five interior triangles, thus you first need to divide the total area by 
The solution is:

So, area of one of the five interior triangles is equal to: 
Now, apply the area formula:



A regular pentagon must have five equivalent sides and five equivalent interior angles. Regular pentagons can be divided up into five equivalent interior triangles, where the base of the triangle is a side length and the height of the triangle is the apothem. This problem provides the total area for the pentagon.
Therefore, you must work backwards using the area formula: 
The solution is:
So, area of one of the five interior triangles is equal to:
Now, apply the area formula:
Compare your answer with the correct one above
Find the area of the regular pentagon.

Find the area of the regular pentagon.


Recall that the area of regular polygons can be found using the following formula:

First, find the perimeter of the pentagon. Since it is a regular pentagon, we can use the following formula to find its perimeter:

Substitute in the length of the given side of the pentagon in order to find the perimeter.


Next, substitute in the given and calculated information to find the area of the pentagon.



Recall that the area of regular polygons can be found using the following formula:
First, find the perimeter of the pentagon. Since it is a regular pentagon, we can use the following formula to find its perimeter:
Substitute in the length of the given side of the pentagon in order to find the perimeter.
Next, substitute in the given and calculated information to find the area of the pentagon.
Compare your answer with the correct one above
The angles at 3 verticies of a pentagon are 60, 80 and 100. Which of the following could NOT be the measures of the other 2 angles?
The angles at 3 verticies of a pentagon are 60, 80 and 100. Which of the following could NOT be the measures of the other 2 angles?
The sum of the angles in a polygon is

For a pentagon, this equals 540. Since the first 3 angles add up to 240, the remaining 2 angles must add up to 
The sum of the angles in a polygon is
For a pentagon, this equals 540. Since the first 3 angles add up to 240, the remaining 2 angles must add up to
Compare your answer with the correct one above
What is the sum of three angles in a hexagon if the perimeter of the hexagon is  ?
?
What is the sum of three angles in a hexagon if the perimeter of the hexagon is 
The perimeter in this question is irrelevant. Use the interior angle formula to determine the total sum of the angles in a hexagon.

There are six interior angles in a hexagon.

Each angle will be a sixth of the total angle.

Therefore, the sum of three angles in a hexagon is:

The perimeter in this question is irrelevant. Use the interior angle formula to determine the total sum of the angles in a hexagon.
There are six interior angles in a hexagon.
Each angle will be a sixth of the total angle.
Therefore, the sum of three angles in a hexagon is:
Compare your answer with the correct one above
Add four interior angles in a regular pentagon. What is the result?
Add four interior angles in a regular pentagon. What is the result?
Use the interior angle formula to find the total sum of angles in a pentagon.

 for a pentagon, so substitute this value into the equation and solve:
for a pentagon, so substitute this value into the equation and solve:

Divide this number by 5, since there are five interior angles.

The sum of four interior angles in a regular pentagon is:

Use the interior angle formula to find the total sum of angles in a pentagon.

Divide this number by 5, since there are five interior angles.
The sum of four interior angles in a regular pentagon is:
Compare your answer with the correct one above
What is the sum of two interior angles of a regular pentagon if the perimeter is 6?
What is the sum of two interior angles of a regular pentagon if the perimeter is 6?
The perimeter of a regular pentagon has no effect on the interior angles of the pentagon.
Use the following formula to solve for the sum of all interior angles in the pentagon.

Since there are 5 sides in a pentagon, substitute the side length  .
.

Divide this by 5 to determine the value of each angle, and then multiply by 2 to determine the sum of 2 interior angles.


The sum of 2 interior angles of a pentagon is  .
.
The perimeter of a regular pentagon has no effect on the interior angles of the pentagon.
Use the following formula to solve for the sum of all interior angles in the pentagon.
Since there are 5 sides in a pentagon, substitute the side length 
Divide this by 5 to determine the value of each angle, and then multiply by 2 to determine the sum of 2 interior angles.
The sum of 2 interior angles of a pentagon is 
Compare your answer with the correct one above
Let the area of a regular pentagon be  . What is the value of an interior angle?
. What is the value of an interior angle?
Let the area of a regular pentagon be 
Area has no effect on the value of the interior angles of a pentagon. To find the sum of all angles of a pentagon, use the following formula, where  is the number of sides:
is the number of sides:

There are 5 sides in a pentagon.

Divide this number by 5 to determine the value of each angle.

Area has no effect on the value of the interior angles of a pentagon. To find the sum of all angles of a pentagon, use the following formula, where 
There are 5 sides in a pentagon.
Divide this number by 5 to determine the value of each angle.
Compare your answer with the correct one above
Suppose an interior angle of a regular pentagon is  . What is
. What is  ?
?
Suppose an interior angle of a regular pentagon is 

The pentagon has 5 sides. To find the value of the interior angle of a pentagon, use the following formula to find the sum of all interior angles.

Substitute  .
.

Divide this number by 5 to determine the value of each interior angle.

Every interior angle is 108 degrees. The problem states that an interior angle is  . Set these two values equal to each other and solve for
. Set these two values equal to each other and solve for  .
.


The pentagon has 5 sides. To find the value of the interior angle of a pentagon, use the following formula to find the sum of all interior angles.
Substitute 
Divide this number by 5 to determine the value of each interior angle.
Every interior angle is 108 degrees. The problem states that an interior angle is 

Compare your answer with the correct one above
True or false: Each of the five angles of a regular pentagon measures  .
.
True or false: Each of the five angles of a regular pentagon measures 
A regular polygon with  sides has
sides has  congruent angles, each of which measures
congruent angles, each of which measures

Setting  , the common angle measure can be calculated to be
, the common angle measure can be calculated to be

The statement is therefore false.
A regular polygon with 

Setting 
The statement is therefore false.
Compare your answer with the correct one above
True or false: Each of the exterior angles of a regular pentagon measures  .
.
True or false: Each of the exterior angles of a regular pentagon measures 
If one exterior angle is taken at each vertex of any polygon, and their measures are added, the sum is  . Each exterior angle of a regular pentagon has the same measure, so if we let
. Each exterior angle of a regular pentagon has the same measure, so if we let  be that common measure, then
be that common measure, then

Solve for  :
:


The statement is true.
If one exterior angle is taken at each vertex of any polygon, and their measures are added, the sum is 

Solve for 
The statement is true.
Compare your answer with the correct one above
Given: Pentagon  .
.

True, false, or undetermined: Pentagon  is regular.
is regular.
Given: Pentagon 
True, false, or undetermined: Pentagon 
Suppose Pentagon  is regular. Each angle of a regular polygon of
is regular. Each angle of a regular polygon of  sides has measure
sides has measure

A pentagon has 5 sides, so set  ; each angle of the regular hexagon has measure
; each angle of the regular hexagon has measure

Since one angle is given to be of measure  , the pentagon might be regular - but without knowing more, it cannot be determined for certain. Therefore, the correct choice is "undetermined".
, the pentagon might be regular - but without knowing more, it cannot be determined for certain. Therefore, the correct choice is "undetermined".
Suppose Pentagon 

A pentagon has 5 sides, so set 
Since one angle is given to be of measure 
Compare your answer with the correct one above
A regular pentagon has a side length of  and an apothem length of
and an apothem length of  . Find the area of the pentagon.
. Find the area of the pentagon.
A regular pentagon has a side length of 

By definition a regular pentagon must have  equal sides and
equal sides and  equivalent interior angles.
equivalent interior angles.
This question provides the length of the apothem of the pentagon--which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into  equivalent interior triangles. Each triangle will have a base of
equivalent interior triangles. Each triangle will have a base of  and a height of
and a height of  .
.
The area of this pentagon can be found by applying the area of a triangle formula:


Note:  is only the measurement for one of the five interior triangles. Thus, the final solution is:
is only the measurement for one of the five interior triangles. Thus, the final solution is:

By definition a regular pentagon must have 

This question provides the length of the apothem of the pentagon--which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into 


The area of this pentagon can be found by applying the area of a triangle formula:
Note: 
Compare your answer with the correct one above
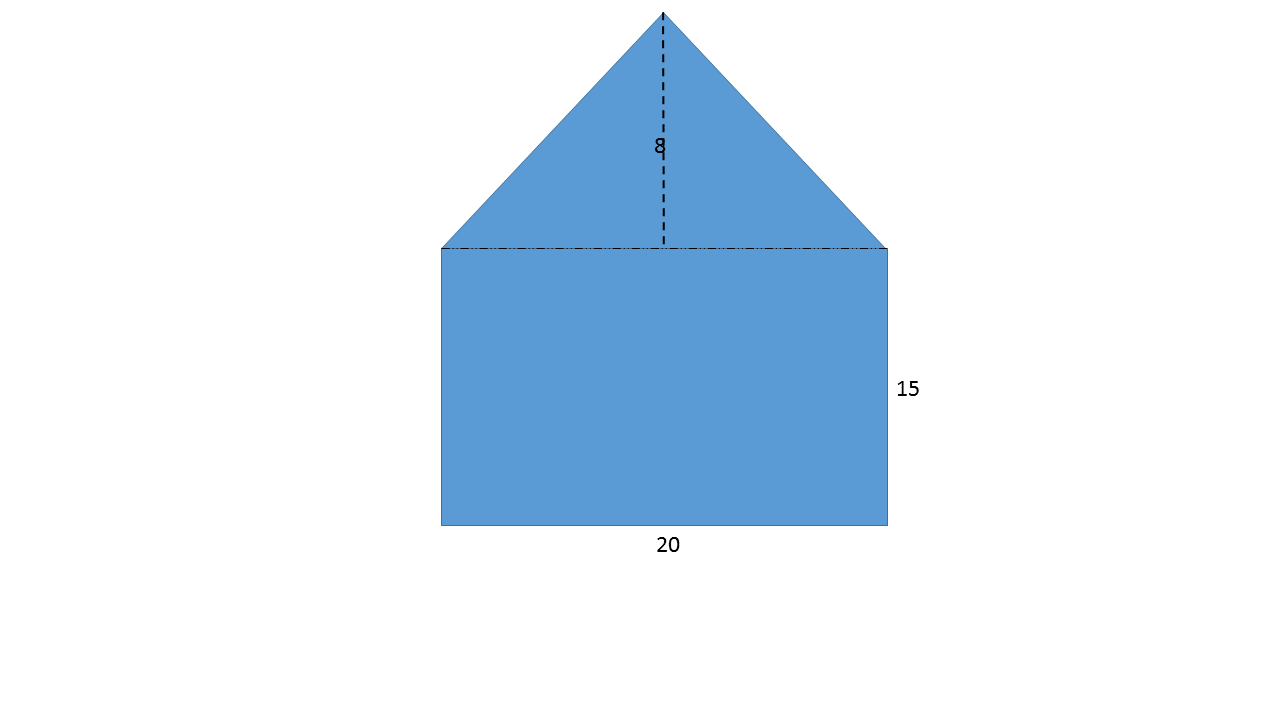
Find the area of the pentagon shown above.

Find the area of the pentagon shown above.
To find the area of this pentagon, divide the interior of the pentagon into a four-sided rectangle and two right triangles. The area of the bottom rectangle can be found using the formula:


The area of the two right triangles can be found using the formula:


Since there are two right triangles, the sum of both will equal the area of the entire triangular top portion of the pentagon.
Thus, the solution is:

To find the area of this pentagon, divide the interior of the pentagon into a four-sided rectangle and two right triangles. The area of the bottom rectangle can be found using the formula:
The area of the two right triangles can be found using the formula:
Since there are two right triangles, the sum of both will equal the area of the entire triangular top portion of the pentagon.
Thus, the solution is:
Compare your answer with the correct one above
A regular pentagon has a perimeter of  yards and an apothem length of
yards and an apothem length of  yards. Find the area of the pentagon.
yards. Find the area of the pentagon.
A regular pentagon has a perimeter of 

To solve this problem, first work backwards using the perimeter formula for a regular pentagon:



Now you have enough information to find the area of this regular triangle.
Note: a regular pentagon must have  equal sides and
equal sides and  equivalent interior angles.
equivalent interior angles.
This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into  equivalent interior triangles. Each triangle will have a base of
equivalent interior triangles. Each triangle will have a base of  and a height of
and a height of  .
.
The area of this pentagon can be found by applying the area of a triangle formula:


Thus, the area of the entire pentagon is:

To solve this problem, first work backwards using the perimeter formula for a regular pentagon:
Now you have enough information to find the area of this regular triangle.
Note: a regular pentagon must have 

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into 


The area of this pentagon can be found by applying the area of a triangle formula:
Thus, the area of the entire pentagon is:
Compare your answer with the correct one above
A regular pentagon has a side length of  and an apothem length of
and an apothem length of  . Find the area of the pentagon.
. Find the area of the pentagon.
A regular pentagon has a side length of 

By definition a regular pentagon must have  equal sides and
equal sides and  equivalent interior angles.
equivalent interior angles.
This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into  equivalent interior triangles. Each triangle will have a base of
equivalent interior triangles. Each triangle will have a base of  and a height of
and a height of  .
.
The area of this pentagon can be found by applying the area of a triangle formula:


Keep in mind that this is the area for only one of the five total interior triangles.
The total area of the pentagon is:

By definition a regular pentagon must have 

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into 


The area of this pentagon can be found by applying the area of a triangle formula:
Keep in mind that this is the area for only one of the five total interior triangles.
The total area of the pentagon is:
Compare your answer with the correct one above
A regular pentagon has a perimeter of  and an apothem length of
and an apothem length of  . Find the area of the pentagon.
. Find the area of the pentagon.
A regular pentagon has a perimeter of 

To solve this problem, first work backwards using the perimeter formula for a regular pentagon:



Now you have enough information to find the area of this regular triangle.
Note: a regular pentagon must have  equal sides and
equal sides and  equivalent interior angles.
equivalent interior angles.
This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into  equivalent interior triangles. Each triangle will have a base of
equivalent interior triangles. Each triangle will have a base of  and a height of
and a height of  .
.
The area of this pentagon can be found by applying the area of a triangle formula:


To find the total area of the pentagon multiply:

To solve this problem, first work backwards using the perimeter formula for a regular pentagon:
Now you have enough information to find the area of this regular triangle.
Note: a regular pentagon must have 

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into 


The area of this pentagon can be found by applying the area of a triangle formula:
To find the total area of the pentagon multiply:
Compare your answer with the correct one above