Quadrilaterals - Math
Card 0 of 316

Find the area of a square with a diagonal of  .
.

Find the area of a square with a diagonal of 
A few facts need to be known to solve this problem. Observe that the diagonal of the square cuts it into two right isosceles triangles; therefore, the length of a side of the square to its diagonal is the same as an isosceles right triangle's leg to its hypotenuse:  .
.


Rearrange an solve for  .
.

Now, solve for the area using the formula  .
.



A few facts need to be known to solve this problem. Observe that the diagonal of the square cuts it into two right isosceles triangles; therefore, the length of a side of the square to its diagonal is the same as an isosceles right triangle's leg to its hypotenuse: 
Rearrange an solve for 
Now, solve for the area using the formula 
Compare your answer with the correct one above
If the ratio of the sides of two squares is  , what is the ratio of the areas of those two squares?
, what is the ratio of the areas of those two squares?
If the ratio of the sides of two squares is 
Express the ratio of the two sides of the squares as  . The area of each square is one side multiplied by itself, so the ratios of the areas would be
. The area of each square is one side multiplied by itself, so the ratios of the areas would be  . The right side of this equation simplifies to a ratio of
. The right side of this equation simplifies to a ratio of  .
.
Express the ratio of the two sides of the squares as 


Compare your answer with the correct one above
What is the area of a square with a diagonal of  ?
?
What is the area of a square with a diagonal of 
The formula for the area of a square is  . However, the problem gives us a diagonal and not a side.
. However, the problem gives us a diagonal and not a side.
Remember that all sides of a square are equal, so the diagonal cuts the square into two equal triangles, each a  right triangle.
right triangle.
If we use the Pythagorean Theorem, we see:


Plug in our given diagonal to solve.





From here we can plug our answer back into our original equation:



The formula for the area of a square is 
Remember that all sides of a square are equal, so the diagonal cuts the square into two equal triangles, each a 
If we use the Pythagorean Theorem, we see:
Plug in our given diagonal to solve.
From here we can plug our answer back into our original equation:
Compare your answer with the correct one above
The perimeter of a square is 48. What is the length of its diagonal?
The perimeter of a square is 48. What is the length of its diagonal?
Perimeter = side * 4
48 = side * 4
Side = 12
We can break up the square into two equal right triangles. The diagonal of the sqaure is then the hypotenuse of these two triangles.
Therefore, we can use the Pythagorean Theorem to solve for the diagonal:





Perimeter = side * 4
48 = side * 4
Side = 12
We can break up the square into two equal right triangles. The diagonal of the sqaure is then the hypotenuse of these two triangles.
Therefore, we can use the Pythagorean Theorem to solve for the diagonal:
Compare your answer with the correct one above
What is the length of a diagonal of a square with a side length  ? Round to the nearest tenth.
? Round to the nearest tenth.
What is the length of a diagonal of a square with a side length 
A square is comprised of two 45-45-90 right triangles. The hypotenuse of a 45-45-90 right triangle follows the rule below, where  is the length of the sides.
is the length of the sides.

In this instance,  is equal to 6.
is equal to 6.

A square is comprised of two 45-45-90 right triangles. The hypotenuse of a 45-45-90 right triangle follows the rule below, where 
In this instance, 
Compare your answer with the correct one above
What is the length of the diagonal of a 7-by-7 square? (Round to the nearest tenth.)
What is the length of the diagonal of a 7-by-7 square? (Round to the nearest tenth.)
To find the diagonal of a square we must use the side lengths to create a 90 degree triangle with side lengths of 7 and a hypotenuse which is equal to the diagonal.
We can use the Pythagorean Theorem here to solve for the hypotenuse of a right triangle.
The Pythagorean Theorem states 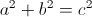 , where a and b are the sidelengths and c is the hypotenuse.
, where a and b are the sidelengths and c is the hypotenuse.
Plug the side lengths into the equation as  and
and  :
:

Square the numbers:

Add the terms on the left side of the equation together:

Take the square root of both sides:


Therefore the length of the diagonal is 9.9.
To find the diagonal of a square we must use the side lengths to create a 90 degree triangle with side lengths of 7 and a hypotenuse which is equal to the diagonal.
We can use the Pythagorean Theorem here to solve for the hypotenuse of a right triangle.
The Pythagorean Theorem states , where a and b are the sidelengths and c is the hypotenuse.
Plug the side lengths into the equation as 

Square the numbers:
Add the terms on the left side of the equation together:
Take the square root of both sides:
Therefore the length of the diagonal is 9.9.
Compare your answer with the correct one above
What is the length of the diagonal of a square with a side length of  ?
?
What is the length of the diagonal of a square with a side length of 
To find the diagonal of a square, we must use the side length to create a 90 degree triangle with side lengths of  ,
,  , and a hypotenuse which is equal to the diagonal.
, and a hypotenuse which is equal to the diagonal.
Pythagorean’s Theorem states 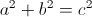 , where a and b are the legs and c is the hypotenuse.
, where a and b are the legs and c is the hypotenuse.
Take  and
and  and plug them into the equation for
and plug them into the equation for  and
and  :
: 
After squaring the numbers, add them together: 
Once you have the sum, take the square root of both sides: 
Simplify to find the answer:  , or
, or  .
.
To find the diagonal of a square, we must use the side length to create a 90 degree triangle with side lengths of 

Pythagorean’s Theorem states , where a and b are the legs and c is the hypotenuse.
Take 



After squaring the numbers, add them together:
Once you have the sum, take the square root of both sides:
Simplify to find the answer: 

Compare your answer with the correct one above
A square has sides of  . What is the length of the diagonal of this square?
. What is the length of the diagonal of this square?
A square has sides of 
To find the diagonal of the square, we effectively cut the square into two  triangles.
triangles.
The pattern for the sides of a  is
is  .
.
Since two sides are equal to  , this triangle will have sides of
, this triangle will have sides of  .
.
Therefore, the diagonal (the hypotenuse) will have a length of  .
.
To find the diagonal of the square, we effectively cut the square into two 
The pattern for the sides of a 

Since two sides are equal to 

Therefore, the diagonal (the hypotenuse) will have a length of 
Compare your answer with the correct one above
A square has sides of  . What is the length of the diagonal of this square?
. What is the length of the diagonal of this square?
A square has sides of 
To find the diagonal of the square, we effectively cut the square into two  triangles.
triangles.
The pattern for the sides of a  is
is  .
.
Since two sides are equal to  , this triangle will have sides of
, this triangle will have sides of  .
.
Therefore, the diagonal (the hypotenuse) will have a length of  .
.
To find the diagonal of the square, we effectively cut the square into two 
The pattern for the sides of a 

Since two sides are equal to 

Therefore, the diagonal (the hypotenuse) will have a length of 
Compare your answer with the correct one above
The area of square R is 12 times the area of square T. If the area of square R is 48, what is the length of one side of square T?
The area of square R is 12 times the area of square T. If the area of square R is 48, what is the length of one side of square T?
We start by dividing the area of square R (48) by 12, to come up with the area of square T, 4. Then take the square root of the area to get the length of one side, giving us 2.
We start by dividing the area of square R (48) by 12, to come up with the area of square T, 4. Then take the square root of the area to get the length of one side, giving us 2.
Compare your answer with the correct one above
When the side of a certain square is increased by 2 inches, the area of the resulting square is 64 sq. inches greater than the original square. What is the length of the side of the original square, in inches?
When the side of a certain square is increased by 2 inches, the area of the resulting square is 64 sq. inches greater than the original square. What is the length of the side of the original square, in inches?
Let x represent the length of the original square in inches. Thus the area of the original square is x2. Two inches are added to x, which is represented by x+2. The area of the resulting square is (x+2)2. We are given that the new square is 64 sq. inches greater than the original. Therefore we can write the algebraic expression:
x2 + 64 = (x+2)2
FOIL the right side of the equation.
x2 + 64 = x2 + 4x + 4
Subtract x2 from both sides and then continue with the alegbra.
64 = 4x + 4
64 = 4(x + 1)
16 = x + 1
15 = x
Therefore, the length of the original square is 15 inches.
If you plug in the answer choices, you would need to add 2 inches to the value of the answer choice and then take the difference of two squares. The choice with 15 would be correct because 172 -152 = 64.
Let x represent the length of the original square in inches. Thus the area of the original square is x2. Two inches are added to x, which is represented by x+2. The area of the resulting square is (x+2)2. We are given that the new square is 64 sq. inches greater than the original. Therefore we can write the algebraic expression:
x2 + 64 = (x+2)2
FOIL the right side of the equation.
x2 + 64 = x2 + 4x + 4
Subtract x2 from both sides and then continue with the alegbra.
64 = 4x + 4
64 = 4(x + 1)
16 = x + 1
15 = x
Therefore, the length of the original square is 15 inches.
If you plug in the answer choices, you would need to add 2 inches to the value of the answer choice and then take the difference of two squares. The choice with 15 would be correct because 172 -152 = 64.
Compare your answer with the correct one above
If the area of a square is 25 inches squared, what is the perimeter?
If the area of a square is 25 inches squared, what is the perimeter?
The area of a square is equal to length times width or length squared (since length and width are equal on a square). Therefore, the length of one side is  or
or  The perimeter of a square is the sum of the length of all 4 sides or
The perimeter of a square is the sum of the length of all 4 sides or 
The area of a square is equal to length times width or length squared (since length and width are equal on a square). Therefore, the length of one side is 

Compare your answer with the correct one above
Two rectangles are similar. The perimeter of the first rectangle is 36. The perimeter of the second is 12. If the base length of the second rectangle is 4, what is the height of the first rectangle?
Two rectangles are similar. The perimeter of the first rectangle is 36. The perimeter of the second is 12. If the base length of the second rectangle is 4, what is the height of the first rectangle?
Solve for the height of the second rectangle.
Perimeter = 2B + 2H
12 = 2(4) + 2H
12 = 8 + 2H
4 = 2H
H = 2
If they are similar, then the base and height are proportionally equal.
B1/H1 = B2/H2
4/2 = B2/H2
2 = B2/H2
B2 = 2H2
Use perimeter equation then solve for H:
Perimeter = 2B + 2H
36 = 2 B2 + 2 H2
36 = 2 (2H2) + 2 H2
36 = 4H2 + 2 H2
36 = 6H2
H2 = 6
Solve for the height of the second rectangle.
Perimeter = 2B + 2H
12 = 2(4) + 2H
12 = 8 + 2H
4 = 2H
H = 2
If they are similar, then the base and height are proportionally equal.
B1/H1 = B2/H2
4/2 = B2/H2
2 = B2/H2
B2 = 2H2
Use perimeter equation then solve for H:
Perimeter = 2B + 2H
36 = 2 B2 + 2 H2
36 = 2 (2H2) + 2 H2
36 = 4H2 + 2 H2
36 = 6H2
H2 = 6
Compare your answer with the correct one above

A square is inscribed inside a circle, as illustrated above. The radius of the circle is  units. If all of the square's diagonals pass through the circle's center, what is the area of the square?
units. If all of the square's diagonals pass through the circle's center, what is the area of the square?

A square is inscribed inside a circle, as illustrated above. The radius of the circle is 
Given that the square's diagonals pass through the circle's center, those diagonals must each form a diameter of the circle. The circle's diameter is twice its radius, i.e.  , which is
, which is  . Since this diameter (i.e., the square's diagonal) is the hypotenuse of a right triangle formed by two sides of the square, the length of one of the square's sides can be calculated with the Pythagorean Theorem.
. Since this diameter (i.e., the square's diagonal) is the hypotenuse of a right triangle formed by two sides of the square, the length of one of the square's sides can be calculated with the Pythagorean Theorem.  replace
replace  and
and  because the sides of the square must be equal in length. Since the objective is to solve for the square's area, solve for
because the sides of the square must be equal in length. Since the objective is to solve for the square's area, solve for  since one side squared will be the square's area.
since one side squared will be the square's area.


 units squared
units squared
Given that the square's diagonals pass through the circle's center, those diagonals must each form a diameter of the circle. The circle's diameter is twice its radius, i.e. 






Compare your answer with the correct one above
The diagonal of a square has a length of 10 inches. What is the perimeter of the square in inches squared?
The diagonal of a square has a length of 10 inches. What is the perimeter of the square in inches squared?
Using the Pythagorean Theorem, we can find the edge of a side to be √50, by 2a2=102. This can be reduced to 5√2. This can then be multiplied by 4 to find the perimeter.
Using the Pythagorean Theorem, we can find the edge of a side to be √50, by 2a2=102. This can be reduced to 5√2. This can then be multiplied by 4 to find the perimeter.
Compare your answer with the correct one above
A circle with a radius 2 in is inscribed in a square. What is the perimeter of the square?
A circle with a radius 2 in is inscribed in a square. What is the perimeter of the square?
To inscribe means to draw inside a figure so as to touch in as many places as possible without overlapping. The circle is inside the square such that the diameter of the circle is the same as the side of the square, so the side is actually 4 in. The perimeter of the square = 4s = 4 * 4 = 16 in.
To inscribe means to draw inside a figure so as to touch in as many places as possible without overlapping. The circle is inside the square such that the diameter of the circle is the same as the side of the square, so the side is actually 4 in. The perimeter of the square = 4s = 4 * 4 = 16 in.
Compare your answer with the correct one above
Square X has 3 times the area of Square Y. If the perimeter of Square Y is 24 ft, what is the area of Square X, in sq ft?
Square X has 3 times the area of Square Y. If the perimeter of Square Y is 24 ft, what is the area of Square X, in sq ft?
Find the area of Square Y, then calculate the area of Square X.
If the perimeter of Square Y is 24, then each side is 24/4, or 6.
A = 6 * 6 = 36 sq ft, for Square Y
If Square X has 3 times the area, then 3 * 36 = 108 sq ft.
Find the area of Square Y, then calculate the area of Square X.
If the perimeter of Square Y is 24, then each side is 24/4, or 6.
A = 6 * 6 = 36 sq ft, for Square Y
If Square X has 3 times the area, then 3 * 36 = 108 sq ft.
Compare your answer with the correct one above
A square garden has an area of 64 square feet. If you add 3 feet to each side, what is the new perimeter of the garden?
A square garden has an area of 64 square feet. If you add 3 feet to each side, what is the new perimeter of the garden?
By finding the square root of the area of the garden, you find the length of one side, which is 8. We add 3 feet to this, giving us 11, then multiply this by 4 to get 44 feet for the perimeter.
By finding the square root of the area of the garden, you find the length of one side, which is 8. We add 3 feet to this, giving us 11, then multiply this by 4 to get 44 feet for the perimeter.
Compare your answer with the correct one above
The area of a square is  . If the square is enlarged by a factor of 2, what is the perimeter of the new square?
. If the square is enlarged by a factor of 2, what is the perimeter of the new square?
The area of a square is 
The area of a square is given by  so we know the side is 5 cm. Enlarging by a factor of two makes the new side 10 cm. The perimeter is given by
so we know the side is 5 cm. Enlarging by a factor of two makes the new side 10 cm. The perimeter is given by  , so the perimeter of the new square is 40 cm.
, so the perimeter of the new square is 40 cm.
The area of a square is given by 

Compare your answer with the correct one above
A square has an area of  . If the side of the square is reduced by a factor of two, what is the perimeter of the new square?
. If the side of the square is reduced by a factor of two, what is the perimeter of the new square?
A square has an area of 
The area of the given square is given by  so the side must be 6 in. The side is reduced by a factor of two, so the new side is 3 in. The perimeter of the new square is given by
so the side must be 6 in. The side is reduced by a factor of two, so the new side is 3 in. The perimeter of the new square is given by  .
.
The area of the given square is given by 

Compare your answer with the correct one above