Spheres - Math
Card 0 of 524
The volume of a sphere is one cubic yard. Give its radius in inches.
The volume of a sphere is one cubic yard. Give its radius in inches.
The volume  of a sphere with radius
of a sphere with radius  is
is
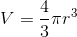 .
.
To find the radius in yards, we set  and solve for
and solve for  .
.


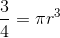


![r = \sqrt[3]{ $\frac{3}{4\pi}$ } = \sqrt[3]{ $\frac{3\cdot 2 $\pi^{2}$$}{4\pi \cdot 2 $\pi^{2}$} }= \sqrt[3]{ $\frac{6 $\pi^{2}$$}{8 $\pi^{3}$} } = $\frac{ \sqrt[3]{6 $\pi^{2}$$} } {2\pi}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/203839/gif.latex) yards.
yards.
Since the problem requests the radius in inches, multiply by 36:
![36 \times $\frac{ \sqrt[3]{6 $\pi^{2}$$} } {2\pi} = $\frac{ 18\sqrt[3]{6 $\pi^{2}$$} } {\pi}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/203840/gif.latex)
The volume 

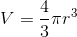
To find the radius in yards, we set 

![r = \sqrt[3]{ $\frac{3}{4\pi}$ } = \sqrt[3]{ $\frac{3\cdot 2 $\pi^{2}$$}{4\pi \cdot 2 $\pi^{2}$} }= \sqrt[3]{ $\frac{6 $\pi^{2}$$}{8 $\pi^{3}$} } = $\frac{ \sqrt[3]{6 $\pi^{2}$$} } {2\pi}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/203839/gif.latex)
Since the problem requests the radius in inches, multiply by 36:
Compare your answer with the correct one above
In terms of  , give the surface area, in square inches, of a spherical water tank with a diameter of 20 feet.
, give the surface area, in square inches, of a spherical water tank with a diameter of 20 feet.
In terms of 
 feet =
feet =  inches, the diameter of the tank; half of this, or 120 inches, is the radius. Set
inches, the diameter of the tank; half of this, or 120 inches, is the radius. Set  , substitute in the surface area formula, and solve for
, substitute in the surface area formula, and solve for  :
:








Compare your answer with the correct one above
Which is the greater quantity?
(a) The surface area of a sphere with radius 1
(b) 12
Which is the greater quantity?
(a) The surface area of a sphere with radius 1
(b) 12
The surface area of a sphere can be found using the formula
 .
.
The surface area of the given sphere can be found by substituting  :
:

 so
so  , or
, or 
This makes (a) greater.
The surface area of a sphere can be found using the formula

The surface area of the given sphere can be found by substituting 


This makes (a) greater.
Compare your answer with the correct one above
Sphere A has volume  . Sphere B has surface area
. Sphere B has surface area  . Which is the greater quantity?
. Which is the greater quantity?
(a) The radius of Sphere A
(b) The radius of Sphere B
Sphere A has volume 

(a) The radius of Sphere A
(b) The radius of Sphere B
(a) Substitute  in the formula for the volume of a sphere:
in the formula for the volume of a sphere:





![r =\sqrt[3]{ 729} = 9](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/149269/gif.latex) inches
inches
(b) Substitute  in the formula for the surface area of a sphere:
in the formula for the surface area of a sphere:




 inches
inches
(b) is greater.
(a) Substitute 
![r =\sqrt[3]{ 729} = 9](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/149269/gif.latex)
(b) Substitute 

(b) is greater.
Compare your answer with the correct one above
 is a positive number. Which is the greater quantity?
is a positive number. Which is the greater quantity?
(A) The surface area of a sphere with radius 
(B) The surface area of a cube with edges of length 

(A) The surface area of a sphere with radius
(B) The surface area of a cube with edges of length
The surface area of a sphere is  times the square of its radius, which here is
times the square of its radius, which here is  ; the surface area of the sphere in (A) is
; the surface area of the sphere in (A) is  .
.
The area of one face of a cube is the square of the length of an edge, which here is  , so the area of one face of the cube in (B) is
, so the area of one face of the cube in (B) is  . The cube has six faces so the total surface area is
. The cube has six faces so the total surface area is  .
.
 , so
, so  , giving the sphere less surface area. (B) is greater.
, giving the sphere less surface area. (B) is greater.
The surface area of a sphere is 


The area of one face of a cube is the square of the length of an edge, which here is 




Compare your answer with the correct one above
In terms of  , give the volume, in cubic feet, of a spherical tank with diameter 36 inches.
, give the volume, in cubic feet, of a spherical tank with diameter 36 inches.
In terms of 
36 inches =  feet, the diameter of the tank. Half of this, or
feet, the diameter of the tank. Half of this, or  feet, is the radius. Set
feet, is the radius. Set  , substitute in the volume formula, and solve for
, substitute in the volume formula, and solve for  :
:





36 inches = 



Compare your answer with the correct one above
Which is the greater quantity?
(a) The volume of a sphere with radius 
(b) The volume of a cube with sidelength 
Which is the greater quantity?
(a) The volume of a sphere with radius
(b) The volume of a cube with sidelength
A sphere with radius  has diameter
has diameter  and can be inscribed inside a cube of sidelength
and can be inscribed inside a cube of sidelength  . Therefore, the cube in (b) has the greater volume.
. Therefore, the cube in (b) has the greater volume.
A sphere with radius 


Compare your answer with the correct one above
Which is the greater quantity?
(a) The volume of a cube with sidelength  inches.
inches.
(b) The volume of a sphere with radius  inches.
inches.
Which is the greater quantity?
(a) The volume of a cube with sidelength inches.
(b) The volume of a sphere with radius inches.
You do not need to calculate the volumes of the figures. All you need to do is observe that a sphere with radius  inches has diameter
inches has diameter  inches, and can therefore be inscribed inside the cube with sidelength
inches, and can therefore be inscribed inside the cube with sidelength  inches. This give the cube larger volume, making (a) the greater quantity.
inches. This give the cube larger volume, making (a) the greater quantity.
You do not need to calculate the volumes of the figures. All you need to do is observe that a sphere with radius inches has diameter
inches, and can therefore be inscribed inside the cube with sidelength
inches. This give the cube larger volume, making (a) the greater quantity.
Compare your answer with the correct one above
Which is the greater quantity?
(a) The volume of a sphere with diameter one foot
(b) 
Which is the greater quantity?
(a) The volume of a sphere with diameter one foot
(b)
The radius of the sphere is one half of its diameter of one foot, which is six inches, so substitute  :
:



 cubic inches,
cubic inches,
which is greater than  .
.
The radius of the sphere is one half of its diameter of one foot, which is six inches, so substitute 

which is greater than 
Compare your answer with the correct one above
 is a positive number. Which is the greater quantity?
is a positive number. Which is the greater quantity?
(A) The volume of a cube with edges of length 
(B) The volume of a sphere with radius 

(A) The volume of a cube with edges of length
(B) The volume of a sphere with radius
No calculation is really needed here, as a sphere with radius  - and, subsequently, diameter
- and, subsequently, diameter  - can be inscribed inside a cube of sidelength
- can be inscribed inside a cube of sidelength  . This makes (A), the volume of the cube, the greater.
. This makes (A), the volume of the cube, the greater.
No calculation is really needed here, as a sphere with radius 


Compare your answer with the correct one above
Which is the greater quantity?
(a) The radius of a sphere with surface area 
(b) The radius of a sphere with volume 
Which is the greater quantity?
(a) The radius of a sphere with surface area
(b) The radius of a sphere with volume
The formula for the surface area of a sphere, given its radius  , is
, is

The sphere in (a) has surface area  , so
, so




The formula for the volume of a sphere, given its radius  , is
, is

The sphere in (b) has volume  , so
, so





![r = \sqrt[3]{27} = 3](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/658471/gif.latex)
The radius of both spheres is 3.
The formula for the surface area of a sphere, given its radius 
The sphere in (a) has surface area 
The formula for the volume of a sphere, given its radius 
The sphere in (b) has volume 
The radius of both spheres is 3.
Compare your answer with the correct one above
Find the diameter of a sphere if the volume is  .
.
Find the diameter of a sphere if the volume is 
Write the volume for the sphere.

Substitute the volume and solve for the radius.



![r=\sqrt[3]{$\frac{3}{4}$\pi}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/295720/gif.latex)
Double the radius to find diameter.
![d=2\sqrt[3]{$\frac{3}{4}$\pi}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/295721/gif.latex)
Write the volume for the sphere.
Substitute the volume and solve for the radius.
Double the radius to find diameter.
Compare your answer with the correct one above
The surface area of a sphere is  . What is the diameter of the sphere?
. What is the diameter of the sphere?
The surface area of a sphere is 
The surface area of a sphere is given by 
So the equation to sovle becomes  or
or  so
so 
To answer the question we need to find the diameter:

The surface area of a sphere is given by
So the equation to sovle becomes 

To answer the question we need to find the diameter:
Compare your answer with the correct one above
A company wants to construct an advertising balloon spherical in shape. It can afford to buy 28,000 square meters of material to make the balloon. What is the largest possible diameter of this balloon (nearest whole meter)?
A company wants to construct an advertising balloon spherical in shape. It can afford to buy 28,000 square meters of material to make the balloon. What is the largest possible diameter of this balloon (nearest whole meter)?
This is equivalent to asking the diameter of a balloon with surface area 28,000 square meters.
The relationship between the surface area  and the radius
and the radius  is:
is:

To find the radius, substitute for the surface area, then solve:



To find the diameter  , double the radius—this is 94.
, double the radius—this is 94.
This is equivalent to asking the diameter of a balloon with surface area 28,000 square meters.
The relationship between the surface area 

To find the radius, substitute for the surface area, then solve:
To find the diameter 
Compare your answer with the correct one above
If the volume of a sphere is  , what is the sphere's diameter?
, what is the sphere's diameter?
If the volume of a sphere is 
Write the formula for the volume of a sphere:

Plug in the volume and find the radius by solving for  :
:

Start solving for  by multiplying both sides of the equation by
by multiplying both sides of the equation by  :
:


Now, divide each side of the equation by  :
:


Reduce the left side of the equation:

Finally, take the cubed root of both sides of the equation:
![\sqrt[3]{$\frac{3}{2\pi}$}=r](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/284622/gif.latex)
Keep in mind that you've solved for the radius, not the diameter. The diameter is double the radius, which is: ![2\sqrt[3]{$\frac{3}{2\pi}$}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/284623/gif.latex) .
.
Write the formula for the volume of a sphere:
Plug in the volume and find the radius by solving for 
Start solving for 

Now, divide each side of the equation by 
Reduce the left side of the equation:
Finally, take the cubed root of both sides of the equation:
Keep in mind that you've solved for the radius, not the diameter. The diameter is double the radius, which is: ![2\sqrt[3]{$\frac{3}{2\pi}$}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/284623/gif.latex)
Compare your answer with the correct one above
The circumference of a sphere is  . Find the radius.
. Find the radius.
The circumference of a sphere is 
If the circumference of a sphere is  , that means we can easily solve for the diameter by using
, that means we can easily solve for the diameter by using  . This is the equation to find the circumference.
. This is the equation to find the circumference.
By substituting in the value for circumference ( ), we can solve for the missing variable
), we can solve for the missing variable  :
:



To find the radius of the sphere, we need to divide this value by  :
:

If the circumference of a sphere is 

By substituting in the value for circumference (

To find the radius of the sphere, we need to divide this value by 
Compare your answer with the correct one above
Find the diameter of a sphere if the volume is  .
.
Find the diameter of a sphere if the volume is 
Write the formula for the volume of a sphere.

Plug in the given volume and solve for the radius.


![r=\sqrt[3]{$\frac{3}{4}$}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/295726/gif.latex)
The diameter is double the radius.
![d=2\sqrt[3]{$\frac{3}{4}$}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/295727/gif.latex)
Write the formula for the volume of a sphere.
Plug in the given volume and solve for the radius.
The diameter is double the radius.
Compare your answer with the correct one above
Find the diameter of a sphere with the volume listed below.

Find the diameter of a sphere with the volume listed below.
In order to solve, we must the given volume into the volume formula for a sphere.


Divide both sides by pi.

Multiply both sides by 3.

Take the cube root of both sides to find the radius.

Double the radius to get the diameter, diameter is 12.
In order to solve, we must the given volume into the volume formula for a sphere.
Divide both sides by pi.
Multiply both sides by 3.
Take the cube root of both sides to find the radius.
Double the radius to get the diameter, diameter is 12.
Compare your answer with the correct one above
Find the diameter of a sphere if it has a volume of  .
.
Find the diameter of a sphere if it has a volume of 
Recall how to find the volume of a sphere:
 , where
, where  is the radius of the sphere.
is the radius of the sphere.
Now, since the radius is half the diameter, the equation for the volume of a sphere can be rewritten as thus:
 , where
, where  is the diameter of the sphere.
is the diameter of the sphere.
Rewrite the equation to solve for  .
.

![d=\sqrt[3]{$\frac{6(\text{Volume of Sphere}$)}{\pi}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/768606/gif.latex)
Now, plug in the volume of the sphere to find the diameter.
![d=\sqrt[3]{$\frac{6(16\pi)}{\pi}$}=4.58](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/768607/gif.latex)
Recall how to find the volume of a sphere:


Now, since the radius is half the diameter, the equation for the volume of a sphere can be rewritten as thus:


Rewrite the equation to solve for 
Now, plug in the volume of the sphere to find the diameter.
Compare your answer with the correct one above
Find the diameter of a sphere if it has a volume of  .
.
Find the diameter of a sphere if it has a volume of 
Recall how to find the volume of a sphere:
 , where
, where  is the radius of the sphere.
is the radius of the sphere.
Now, since the radius is half the diameter, the equation for the volume of a sphere can be rewritten as thus:
 , where
, where  is the diameter of the sphere.
is the diameter of the sphere.
Rewrite the equation to solve for  .
.

![d=\sqrt[3]{$\frac{6(\text{Volume of Sphere}$)}{\pi}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/768486/gif.latex)
Now, plug in the volume of the sphere to find the diameter.
![d=\sqrt[3]{$\frac{6(24\pi)}{\pi}$}=5.24](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/768487/gif.latex)
Recall how to find the volume of a sphere:


Now, since the radius is half the diameter, the equation for the volume of a sphere can be rewritten as thus:


Rewrite the equation to solve for 
Now, plug in the volume of the sphere to find the diameter.
Compare your answer with the correct one above