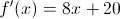Using the Chain Rule

Help Questions

Math › Using the Chain Rule

Questions 1 - 4

1

$\frac{\mathrm{d} }{\mathrm{d} x} \sin(2x)=?$

$2\cos(2x)$

$\cos(2x)$

$-\frac{1}{2}\cos(2x)$

$2\cos(x)$

$2\sin(2x)$

Explanation

For this problem we need to use the chain rule:

$\frac{\mathrm{d} }{\mathrm{d} x}\sin(2x)=\frac{\mathrm{d} }{\mathrm{d} x} \sin(2x)*\frac{\mathrm{d} }{\mathrm{d} x}2x$

$\frac{\mathrm{d} }{\mathrm{d} x}\sin(2x)=\cos(2x)*2$

$\frac{\mathrm{d} }{\mathrm{d} x}\sin(2x)=2\cos(2x)$

2

Find the derivative of the following function:

Explanation

Use -substitution so that .

Then the function becomes .

By the chain rule, $f'(x) = \frac{du}{dx} \times \frac{df}{du}$ .

We calculate each term using the power rule:

$\frac{du}{dx} = 2$

$\frac{df}{du} = 2u$

Plug in :

3

If what is the slope of the line at .

$\infty$

Explanation

The slope at any point on a line is also equal to the derivative. So first we want to find the derivative function of this function and then evaluate it at. So, to find the derivative we will need to use the chain rule. The chain rule says

$\frac{d}{dx}} f(g(x)) = f'(g(x))g'(x)$

so if we let and then

since $f'(x)=\frac{1}{x}}$ and

$\frac{d}{dx}} f(g(x)) = f'(g(x))g'(x) = \frac{1}{x^3}*3x^2 = \frac{3}{x}$

Therefore we evaluate at and we get $\frac{3}{12}$ or .

4

What is the first derivative of ?

Explanation

To solve for the first derivative, we're going to use the chain rule. The chain rule says that when taking the derivative of a nested function, your answer is the derivative of the outside times the derivative of the inside.

Mathematically, it would look like this: $\frac{\mathrm{d} }{\mathrm{d} x}f(g(x))=f'(g(x))*g'(x)$

Plug in our equations.

$\frac{\mathrm{d} }{\mathrm{d} x}(x+6)^2=(2(x+6)^{1})*(1+0)$

$\frac{\mathrm{d} }{\mathrm{d} x}(x+6)^2=(2(x+6))$

$\frac{\mathrm{d} }{\mathrm{d} x}(x+6)^2=2x+12$

Return to subject