Quantum Chemistry - Physical Chemistry
Card 0 of 96
Microwave radiation falls in the wavelength region of  .
.
What is the frequency of microwave radiation that has a wavelength of  ?
?

Microwave radiation falls in the wavelength region of 
What is the frequency of microwave radiation that has a wavelength of 
 , where
, where  is the speed of light,
is the speed of light,  is the wavelength, and
is the wavelength, and  is frequency.
is frequency.





Compare your answer with the correct one above
The wavelength of a particular color of red-orange light is  .
.
What is the frequency of this color?

The wavelength of a particular color of red-orange light is 
What is the frequency of this color?
 , where
, where  is the speed of light,
is the speed of light,  is the wavelength, and
is the wavelength, and  is frequency.
is frequency.





Compare your answer with the correct one above
What is the frequency of microwave radiation that has a wavelength of 0.885m?

What is the frequency of microwave radiation that has a wavelength of 0.885m?
To solve this problem, we use the following equation:

Where  is the wavelength and
is the wavelength and  is the frequency.
is the frequency.
Wavelength is given, and as we are dealing with the electromagnetic spectrum, we know that  is equal to the speed of light, which is given. We need to solve for frequency, so we arrange the equation as follows:
is equal to the speed of light, which is given. We need to solve for frequency, so we arrange the equation as follows: 
Plug in known values and solve.


To solve this problem, we use the following equation:
Where 

Wavelength is given, and as we are dealing with the electromagnetic spectrum, we know that 
Plug in known values and solve.
Compare your answer with the correct one above
The wavelength of a particular color of orange light is 629nm.
What is the frequency of this color?

The wavelength of a particular color of orange light is 629nm.
What is the frequency of this color?
To solve this problem, we use the following equation:

Where  is the wavelength and
is the wavelength and  is the frequency.
is the frequency.
Wavelength is given, and as we are dealing with the electromagnetic spectrum, we know that  is equal to the speed of light, which is given. We need to solve for frequency, so we arrange the equation as follows:
is equal to the speed of light, which is given. We need to solve for frequency, so we arrange the equation as follows: 
Plug in known values and solve.


To solve this problem, we use the following equation:
Where 

Wavelength is given, and as we are dealing with the electromagnetic spectrum, we know that 
Plug in known values and solve.
Compare your answer with the correct one above
A local FM radio station broadcasts at a frequency of 99.0MHz.
What is the wavelength at which the station is broadcasting?

A local FM radio station broadcasts at a frequency of 99.0MHz.
What is the wavelength at which the station is broadcasting?
To solve this problem, we use the following equation:

Where  is the wavelength and
is the wavelength and  is the frequency.
is the frequency.
Rearrange the equation to solve for wavelength.

Plug in known values and solve.


To solve this problem, we use the following equation:
Where 

Rearrange the equation to solve for wavelength.
Plug in known values and solve.
Compare your answer with the correct one above
A researcher analyzes two types of electromagnetic waves. He observes that wave A has a higher amplitude than wave B. What can you conclude about these two waves?
A researcher analyzes two types of electromagnetic waves. He observes that wave A has a higher amplitude than wave B. What can you conclude about these two waves?
Amplitude of a wave is defined as the maximum peak of oscillation or vibration. Recall that frequency, wavelength, and speed are not dependent on the amplitude and are calculated using the wave equation:

Here,  is the speed of the wave (which is the speed of light for electromagnetic waves),
is the speed of the wave (which is the speed of light for electromagnetic waves),  is the frequency, and
is the frequency, and  is the wavelength. Amplitude of a wave is not present in this equation and, therefore, cannot be used to determine relative values of frequency, wavelength, and speed.
is the wavelength. Amplitude of a wave is not present in this equation and, therefore, cannot be used to determine relative values of frequency, wavelength, and speed.
Amplitude of a wave is defined as the maximum peak of oscillation or vibration. Recall that frequency, wavelength, and speed are not dependent on the amplitude and are calculated using the wave equation:
Here, 


Compare your answer with the correct one above
If a star approaches earth the electromagnetic waves from the star are perceived to have shorter wavelength whereas if a star moves away from the earth the waves have longer wavelength.
When observing through a telescope, a scientist notices that star A appears red whereas star B appears blue. Which of the following is true regarding these two stars?
If a star approaches earth the electromagnetic waves from the star are perceived to have shorter wavelength whereas if a star moves away from the earth the waves have longer wavelength.
When observing through a telescope, a scientist notices that star A appears red whereas star B appears blue. Which of the following is true regarding these two stars?
The phenomenon described in this question is called redshift and blueshift. All stars emit electromagnetic waves. The perceived wavelength of these waves depends on the relative motion of the object. If an object is approaching the observer (in this case, the earth) then the apparent wavelength of emitted waves decreases whereas if the object moves away then the apparent wavelength increases. This is called the Doppler effect.
To answer this question, we need to know the relative wavelengths of blue and red light. Blue light has wavelength between  whereas red light has wavelength between
whereas red light has wavelength between  . The question states that star A appears red and star B appears blue. Since red has the higher wavelength, star A is going away from the earth. Similarly, since blue has a lower wavelength, star B is approaching earth.
. The question states that star A appears red and star B appears blue. Since red has the higher wavelength, star A is going away from the earth. Similarly, since blue has a lower wavelength, star B is approaching earth.
Recall that lower wavelength means higher frequency; therefore, blue has the higher frequency.
The phenomenon described in this question is called redshift and blueshift. All stars emit electromagnetic waves. The perceived wavelength of these waves depends on the relative motion of the object. If an object is approaching the observer (in this case, the earth) then the apparent wavelength of emitted waves decreases whereas if the object moves away then the apparent wavelength increases. This is called the Doppler effect.
To answer this question, we need to know the relative wavelengths of blue and red light. Blue light has wavelength between 

Recall that lower wavelength means higher frequency; therefore, blue has the higher frequency.
Compare your answer with the correct one above
Microwave rays have a
wavelength and a
energy than ultraviolet rays.
Microwave rays have a wavelength and a energy than ultraviolet rays.
To solve this question, we need to first recall the electromagnetic spectrum. Microwaves have very large wavelengths. They are found between visible light and radio waves. Ultraviolet, on the other hand, is found below visible light; therefore, ultraviolet rays have smaller wavelength than microwaves.
To solve for energy we need to use the following equation.

Here,  is the energy,
is the energy,  is Planck’s constant,
is Planck’s constant,  is speed of light, and
is speed of light, and  is wavelength. Since energy is inversely proportional to wavelength, higher wavelengths will lead to lower energy. This means that microwaves will have lower energy than ultraviolet rays.
is wavelength. Since energy is inversely proportional to wavelength, higher wavelengths will lead to lower energy. This means that microwaves will have lower energy than ultraviolet rays.
Gamma rays have the lowest wavelength and highest energy whereas radio waves typically have the highest wavelength and lowest energy.
To solve this question, we need to first recall the electromagnetic spectrum. Microwaves have very large wavelengths. They are found between visible light and radio waves. Ultraviolet, on the other hand, is found below visible light; therefore, ultraviolet rays have smaller wavelength than microwaves.
To solve for energy we need to use the following equation.
Here, 



Gamma rays have the lowest wavelength and highest energy whereas radio waves typically have the highest wavelength and lowest energy.
Compare your answer with the correct one above
Two light sources are placed equidistant from a detector. The light from light source A is detected quicker than light from light source B. What can be concluded from these results?
Two light sources are placed equidistant from a detector. The light from light source A is detected quicker than light from light source B. What can be concluded from these results?
The question states that there are two light sources and that both are placed equidistant from a detector. This means that any differences in detection speed is not related to the distance. The question also states that the detector picks up light from source A quicker that light from source B. This means that the speed of the light from source A is faster. Recall that light (or electromagnetic rays) can have varying wavelengths and frequencies; however, the speed of all electromagnetic rays is the same. It doesn’t matter if it is gamma rays or visible light, the speed of light in air is  . The information given in this question contradicts this; therefore, these results are invalid.
. The information given in this question contradicts this; therefore, these results are invalid.
We cannot determine the color of the light for the light sources because we don't have any information regarding their respective wavelength or frequency. The number of photons per unit time refers to the amplitude of the wave, which also cannot be determined from the given information.
The question states that there are two light sources and that both are placed equidistant from a detector. This means that any differences in detection speed is not related to the distance. The question also states that the detector picks up light from source A quicker that light from source B. This means that the speed of the light from source A is faster. Recall that light (or electromagnetic rays) can have varying wavelengths and frequencies; however, the speed of all electromagnetic rays is the same. It doesn’t matter if it is gamma rays or visible light, the speed of light in air is 
We cannot determine the color of the light for the light sources because we don't have any information regarding their respective wavelength or frequency. The number of photons per unit time refers to the amplitude of the wave, which also cannot be determined from the given information.
Compare your answer with the correct one above
Photons in ultraviolet rays have a wavelength of 10nm. What is the energy of photons in radio waves?
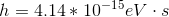
Photons in ultraviolet rays have a wavelength of 10nm. What is the energy of photons in radio waves?
To solve this question, we need to use the equation relating energy of a wave to its wavelength.

Here,  is the energy,
is the energy,  is Planck’s constant,
is Planck’s constant,  is speed of light (for us it’s always
is speed of light (for us it’s always  ), and
), and  is the wavelength (in meters). The energy of the ultraviolet rays is
is the wavelength (in meters). The energy of the ultraviolet rays is


If we look at the electromagnetic spectrum we will notice that the wavelength of radio waves is a lot higher than ultraviolet rays. Since energy is inversely proportional to wavelength we can conclude that the energy of radio waves is lower than ultraviolet's. The only answer choice with an energy lower than ultraviolet rays energy is 1.24neV.
To solve this question, we need to use the equation relating energy of a wave to its wavelength.
Here, 




If we look at the electromagnetic spectrum we will notice that the wavelength of radio waves is a lot higher than ultraviolet rays. Since energy is inversely proportional to wavelength we can conclude that the energy of radio waves is lower than ultraviolet's. The only answer choice with an energy lower than ultraviolet rays energy is 1.24neV.
Compare your answer with the correct one above
Which of the following is/are the same for photons in gamma rays and in visible light?
I. frequency
II. wavelength
III. speed
Which of the following is/are the same for photons in gamma rays and in visible light?
I. frequency
II. wavelength
III. speed
Electromagnetic spectrum is a spectrum of different types of light. Each type of electromagnetic wave differs from one another based on the frequency and wavelength; however, the speed of every electromagnetic wave in air is  . The wave equation relates the speed of an electromagnetic to its wavelength and frequency as follows.
. The wave equation relates the speed of an electromagnetic to its wavelength and frequency as follows.

Here,  is speed of light,
is speed of light,  is wavelength, and
is wavelength, and  is frequency. Since
is frequency. Since  is always constant, wavelength and frequency are inversely proportional to each other. This means that if the wavelength increases the frequency decreases.
is always constant, wavelength and frequency are inversely proportional to each other. This means that if the wavelength increases the frequency decreases.
Electromagnetic spectrum is a spectrum of different types of light. Each type of electromagnetic wave differs from one another based on the frequency and wavelength; however, the speed of every electromagnetic wave in air is 
Here, 



Compare your answer with the correct one above
What is the maximum number of electrons possible with n = 4 in an atom?
What is the maximum number of electrons possible with n = 4 in an atom?
The types of subshells, from smallest to largest, are as follows: s, p, d, and f. These four subshells correspond respectively to the following quantum numbers: 0, 1, 2, and 3. The total number of orbitals in an atom with n = 4 is 42 or 16: one 4s , three 4p , five 4d and seven 4f. Each orbital can hold a maximum of 2 electrons. Therefore, the maximum number of electrons possible is 32.
The types of subshells, from smallest to largest, are as follows: s, p, d, and f. These four subshells correspond respectively to the following quantum numbers: 0, 1, 2, and 3. The total number of orbitals in an atom with n = 4 is 42 or 16: one 4s , three 4p , five 4d and seven 4f. Each orbital can hold a maximum of 2 electrons. Therefore, the maximum number of electrons possible is 32.
Compare your answer with the correct one above
How many sublevels are there with n = 2 in an atom?
How many sublevels are there with n = 2 in an atom?
The types of subshells, from smallest to largest, are as follows: s, p, d, and f. These four subshells correspond respectively to the following quantum numbers: 0, 1, 2, and 3. The total number of orbitals in an atom with n = 3 is 32 or 9: one 3s , three 3p and five 3d. Each orbital can hold a maximum of 2 electrons. Therefore, the maximum number of electrons possible is 2 x 9 = 18.
The types of subshells, from smallest to largest, are as follows: s, p, d, and f. These four subshells correspond respectively to the following quantum numbers: 0, 1, 2, and 3. The total number of orbitals in an atom with n = 3 is 32 or 9: one 3s , three 3p and five 3d. Each orbital can hold a maximum of 2 electrons. Therefore, the maximum number of electrons possible is 2 x 9 = 18.
Compare your answer with the correct one above
Which of the following sets of quantum numbers ( ) could correspond to a
) could correspond to a  orbital?
orbital?
Which of the following sets of quantum numbers (

Since we're looking at the  orbital, we know
orbital, we know  . The range of possible values for
. The range of possible values for  is 0 to
is 0 to  . Possible values for
. Possible values for  range
range  to
to  . Therefore, among the answer choices,
. Therefore, among the answer choices,  is the only possible combination of quantum numbers corresponding to an
is the only possible combination of quantum numbers corresponding to an  orbital.
orbital.
Since we're looking at the 








Compare your answer with the correct one above
Which of the following sets of quantum numbers could correspond to a  orbital?
orbital?
Which of the following sets of quantum numbers could correspond to a 
Since we're looking at the  orbital, we know
orbital, we know  . The range of possible values for
. The range of possible values for  is 0 to
is 0 to  . Possible values for
. Possible values for  range
range  to
to  . Therefore, among the answer choices,
. Therefore, among the answer choices,



is the only possible combination of quantum numbers corresponding to a  orbital.
orbital.
Since we're looking at the 






is the only possible combination of quantum numbers corresponding to a 
Compare your answer with the correct one above
How many subshells are there with n = 4 in an atom?
How many subshells are there with n = 4 in an atom?
The types of subshells, from smallest to largest, are as follows: s, p, d, and f. These four subshells correspond respectively to the following quantum numbers: 0, 1, 2, and 3. The total number of sublevels with n = 4 is n or 4: 4s, 4p, 4d and 4f.
The types of subshells, from smallest to largest, are as follows: s, p, d, and f. These four subshells correspond respectively to the following quantum numbers: 0, 1, 2, and 3. The total number of sublevels with n = 4 is n or 4: 4s, 4p, 4d and 4f.
Compare your answer with the correct one above
Which of the following is/are true regarding the principal quantum number?
I. Principal quantum number signifies the energy level
II. Principal quantum number can never equal zero
III. Principal quantum number can be positive or negative
Which of the following is/are true regarding the principal quantum number?
I. Principal quantum number signifies the energy level
II. Principal quantum number can never equal zero
III. Principal quantum number can be positive or negative
Quantum numbers are fancy coordinate systems that describe the potential location of an electron within an atom. The first quantum number is called the principal quantum number and it signifies the shell the electron is located in. Recall that electron shells are discrete orbits in an atom that have discrete energy; therefore, the principal quantum number signifies the energy level of an electron.
The principal quantum number is always an integer and is always greater than zero. If  the electron is found within the first shell, if
the electron is found within the first shell, if  then the electron is found within the second shell, and so and and so forth. Also, since it is always greater than zero, the principal quantum number can never be negative.
then the electron is found within the second shell, and so and and so forth. Also, since it is always greater than zero, the principal quantum number can never be negative.
Quantum numbers are fancy coordinate systems that describe the potential location of an electron within an atom. The first quantum number is called the principal quantum number and it signifies the shell the electron is located in. Recall that electron shells are discrete orbits in an atom that have discrete energy; therefore, the principal quantum number signifies the energy level of an electron.
The principal quantum number is always an integer and is always greater than zero. If 

Compare your answer with the correct one above
What can be concluded about the quantum numbers for potassium and potassium ion?
What can be concluded about the quantum numbers for potassium and potassium ion?
Potassium has one valence electron. This means that there is one electron in its outermost shell (4th shell). Potassium ion, on the other hand, loses an electron and has a complete octet (has eight valence electrons) in its 3rd shell. Recall that the principal quantum number signifies the shell. Since the valence electron of potassium is found in the fourth shell,  . Similarly, the valence electrons of potassium ion are found in the third shell and
. Similarly, the valence electrons of potassium ion are found in the third shell and  for them. Valence electron of potassium has the higher principal quantum number.
for them. Valence electron of potassium has the higher principal quantum number.
Orbital angular momentum number ( ) is the second quantum number and it signifies the type of orbital. It is always greater than or equal to zero. There are four main types of orbital: s, p, d, and f. Each orbital can hold two electrons. In a given shell, there are one ‘s’ orbital, three ‘p’ orbitals, five ‘d’ orbitals, and seven ‘f’ orbitals. ‘l’ = 0 for ‘s’ orbitals, ‘l’ = 1 for ‘p’ orbitals, ‘l’ = 2 for ‘d’ orbitals, and ‘l’ = 3 for ‘f’ orbitals. In potassium, there is only one valence electron; therefore, there is only one electron in the fourth shell and it can fit into the ‘s’ orbital. In potassium ion, there are eight valence electrons; therefore, two electrons can be found in the ‘s’ orbital and the remaining six electrons can be found in the three ‘p’ orbitals. Not all valence electrons of potassium ion and potassium have different ‘l’ value. This is because valence electron of potassium and two of the valence electrons of potassium ion are found in the ‘s’ orbital (
) is the second quantum number and it signifies the type of orbital. It is always greater than or equal to zero. There are four main types of orbital: s, p, d, and f. Each orbital can hold two electrons. In a given shell, there are one ‘s’ orbital, three ‘p’ orbitals, five ‘d’ orbitals, and seven ‘f’ orbitals. ‘l’ = 0 for ‘s’ orbitals, ‘l’ = 1 for ‘p’ orbitals, ‘l’ = 2 for ‘d’ orbitals, and ‘l’ = 3 for ‘f’ orbitals. In potassium, there is only one valence electron; therefore, there is only one electron in the fourth shell and it can fit into the ‘s’ orbital. In potassium ion, there are eight valence electrons; therefore, two electrons can be found in the ‘s’ orbital and the remaining six electrons can be found in the three ‘p’ orbitals. Not all valence electrons of potassium ion and potassium have different ‘l’ value. This is because valence electron of potassium and two of the valence electrons of potassium ion are found in the ‘s’ orbital ( ).
).
Electrons found in higher shell numbers have higher energy. Valence electron of potassium is found in the fourth shell; therefore, it will have a higher energy than any of the valence electrons of potassium ion.
Potassium has one valence electron. This means that there is one electron in its outermost shell (4th shell). Potassium ion, on the other hand, loses an electron and has a complete octet (has eight valence electrons) in its 3rd shell. Recall that the principal quantum number signifies the shell. Since the valence electron of potassium is found in the fourth shell, 

Orbital angular momentum number (

Electrons found in higher shell numbers have higher energy. Valence electron of potassium is found in the fourth shell; therefore, it will have a higher energy than any of the valence electrons of potassium ion.
Compare your answer with the correct one above
Consider the following descriptions of quantum numbers:
A: energy level within a subshell
B: shape of orbital
C: spin of electron
D: energy level
Which of the following is the correct pairing of quantum numbers (1st, 2nd, 3rd, and 4th) with the given descriptions?
Consider the following descriptions of quantum numbers:
A: energy level within a subshell
B: shape of orbital
C: spin of electron
D: energy level
Which of the following is the correct pairing of quantum numbers (1st, 2nd, 3rd, and 4th) with the given descriptions?
There are four quantum numbers. The first quantum, or principal quantum number, is designated by the letter ‘n’. It signifies the electron shell, or the energy level of the electron. The second quantum number, or orbital angular momentum quantum number, is designated by the letter ‘l’. It signifies the shape (or type) of the orbital. The third quantum number, or magnetic quantum number, is designated by  . This signifies the energy level within a subshell. Each orbital can be located in different orientations in space. For example, each of the three ‘p’ orbitals are oriented differently in space and have different energy levels. The third quantum number describes this phenomenon. Finally, the fourth quantum number, or spin quantum number, is designated by
. This signifies the energy level within a subshell. Each orbital can be located in different orientations in space. For example, each of the three ‘p’ orbitals are oriented differently in space and have different energy levels. The third quantum number describes this phenomenon. Finally, the fourth quantum number, or spin quantum number, is designated by  and describes the spin of the electron. An electron can spin clockwise or counterclockwise.
and describes the spin of the electron. An electron can spin clockwise or counterclockwise.  describes the direction of the spin. Since an electron can only rotate two ways,
describes the direction of the spin. Since an electron can only rotate two ways,  can only be two values
can only be two values  or
or  .
.
These four numbers together describe the potential location of an electron inside an atom. Note that no two electrons can have the same set of quantum numbers (meaning at least one of the four numbers will be different).
There are four quantum numbers. The first quantum, or principal quantum number, is designated by the letter ‘n’. It signifies the electron shell, or the energy level of the electron. The second quantum number, or orbital angular momentum quantum number, is designated by the letter ‘l’. It signifies the shape (or type) of the orbital. The third quantum number, or magnetic quantum number, is designated by 





These four numbers together describe the potential location of an electron inside an atom. Note that no two electrons can have the same set of quantum numbers (meaning at least one of the four numbers will be different).
Compare your answer with the correct one above
Which of the following is true regarding ethene? (The electrons in answer choices refer to carbon electrons)
Which of the following is true regarding ethene? (The electrons in answer choices refer to carbon electrons)
Ethene, or  , has a carbon-carbon single (
, has a carbon-carbon single ( ) and double (
) and double ( ) bond. Recall that a
) bond. Recall that a  bond can be found in hybridized orbitals whereas a
bond can be found in hybridized orbitals whereas a  bond cannot. This means that the carbon atoms in ethene hybridize the single ‘s’ orbital and two of the ‘p’ orbitals, forming a
bond cannot. This means that the carbon atoms in ethene hybridize the single ‘s’ orbital and two of the ‘p’ orbitals, forming a  hybridization. The
hybridization. The  bonds (
bonds ( ) are found in these three hybridized orbitals. The remaining unhybridized ‘p’ orbital will house the two electrons in the
) are found in these three hybridized orbitals. The remaining unhybridized ‘p’ orbital will house the two electrons in the  bond.
bond.
The orbital angular momentum number is the second quantum number and it signifies the type of orbital. An electron found in a ‘p’ orbital will always have an  . Since both electrons in the
. Since both electrons in the  bond are found in the ‘p’ orbital, the ‘l’ value for both electrons is the same.
bond are found in the ‘p’ orbital, the ‘l’ value for both electrons is the same.
The principal quantum number is the first quantum number and it signifies the shell or energy level of an electron. All electrons involved in bonds are found in carbon’s outermost shell (2nd shell); therefore, they will all have an  . Remember that no two electrons can have the same set of quantum numbers (regardless of whether the electrons are found as lone pairs, in
. Remember that no two electrons can have the same set of quantum numbers (regardless of whether the electrons are found as lone pairs, in  bonds, or in
bonds, or in  bonds).
bonds).
Ethene, or 








The orbital angular momentum number is the second quantum number and it signifies the type of orbital. An electron found in a ‘p’ orbital will always have an 

The principal quantum number is the first quantum number and it signifies the shell or energy level of an electron. All electrons involved in bonds are found in carbon’s outermost shell (2nd shell); therefore, they will all have an 


Compare your answer with the correct one above