Mechanics - Physics
Card 0 of 228
A toy car is set up on a frictionless track containing a downward sloping ramp and a vertically oriented loop. Assume the ramp is  tall. The car starts at the top of the ramp at rest.
tall. The car starts at the top of the ramp at rest.
What additional piece of information is necessary to calculate the maximum height of the loop if the car is to complete the loop and continue out the other side?
A toy car is set up on a frictionless track containing a downward sloping ramp and a vertically oriented loop. Assume the ramp is 
What additional piece of information is necessary to calculate the maximum height of the loop if the car is to complete the loop and continue out the other side?
This is an example of conservation of energy. The car starts at the top of the ramp, at height  . It has no velocity at this time since it is starting from a rest. Therefore its total energy is
. It has no velocity at this time since it is starting from a rest. Therefore its total energy is  where
where  is the mass of the car and
is the mass of the car and  is the value of gravitational acceleration.
is the value of gravitational acceleration.
At the bottom of the loop, all of the potential energy will have been converted into kinetic energy.
As the car traverses the loop and rises above the ground, kinetic energy will be converted back into potential energy. The shape of the loop does not matter in this case -- only the vertical distance between the ground and the car.
In the tallest possible loop, all kinetic energy at the bottom is converted to potential energy at the top. This is the maximum height the car can reach -- there is no additional energy left to continue climbing a taller loop. Therefore, the potential energy at the top of the tallest loop we can build is equal to the kinetic energy at the bottom of the loop. But we have already noted that the kinetic energy at the bottom of the loop is equal to the potential energy at the top of the ramp.
Therefore, we set  . We see that
. We see that  and
and  cancel, and we are left with
cancel, and we are left with  . In other words, the tallest loop you can build is equal to the height of whatever ramp you select. In this example, the tallest loop we can build is
. In other words, the tallest loop you can build is equal to the height of whatever ramp you select. In this example, the tallest loop we can build is  . We do not need to know the specific values of
. We do not need to know the specific values of  or
or  .
.
This is an example of conservation of energy. The car starts at the top of the ramp, at height 



At the bottom of the loop, all of the potential energy will have been converted into kinetic energy.
As the car traverses the loop and rises above the ground, kinetic energy will be converted back into potential energy. The shape of the loop does not matter in this case -- only the vertical distance between the ground and the car.
In the tallest possible loop, all kinetic energy at the bottom is converted to potential energy at the top. This is the maximum height the car can reach -- there is no additional energy left to continue climbing a taller loop. Therefore, the potential energy at the top of the tallest loop we can build is equal to the kinetic energy at the bottom of the loop. But we have already noted that the kinetic energy at the bottom of the loop is equal to the potential energy at the top of the ramp.
Therefore, we set 






Compare your answer with the correct one above
An elevator is designed to hold  of cargo. The designers want the elevator to be able to go from the ground floor to the top of a
of cargo. The designers want the elevator to be able to go from the ground floor to the top of a  tall building in
tall building in  . What is the minimum amount of power that must be delivered to the motor at the top of the shaft? Assume no friction and that the elevator itself has a negligible weight.
. What is the minimum amount of power that must be delivered to the motor at the top of the shaft? Assume no friction and that the elevator itself has a negligible weight.
An elevator is designed to hold 


Power is the rate of energy transfer. To raise a  object
object  , a total of
, a total of  or (
or ( is required. To find the power in Watts (
is required. To find the power in Watts ( ), we divide the total energy required by the time over which the energy must be transferred:
), we divide the total energy required by the time over which the energy must be transferred:

Power is the rate of energy transfer. To raise a 




Compare your answer with the correct one above
How far can a person jump while running at  and a vertical velocity of
and a vertical velocity of  ?
?
How far can a person jump while running at 

We know that:


and we are looking for the maximum height (vertical displacement) this person can obtain, so we aren't concerned with  .
.
We can apply the conservation of energy:



Masses cancel, so

Solve for  :
:

 (rounded to simplify our calculations)
(rounded to simplify our calculations)
so let's plug in what we know
 . This is our final answer.
. This is our final answer.
We know that:
and we are looking for the maximum height (vertical displacement) this person can obtain, so we aren't concerned with 
We can apply the conservation of energy:
Masses cancel, so
Solve for 

so let's plug in what we know

Compare your answer with the correct one above
If a  object has a kinetic energy of
object has a kinetic energy of  right after it is launched in the air, and it has
right after it is launched in the air, and it has  KE at its max height, what is its max height?
KE at its max height, what is its max height?
If a 


Let's first write down the information we are given:



In order to solve this problem we must apply the conservation of energy, which states  since no friction.
since no friction.
This means that as the project reaches its max height energy is converted from Kinetic Energy (energy of motion) to potential gravitational energy (based off of height).
We can subtract  from
from  to get the
to get the  at its max height
at its max height
 =
=


so we can solve for the height


where 
therefore 
Let's first write down the information we are given:
In order to solve this problem we must apply the conservation of energy, which states 
This means that as the project reaches its max height energy is converted from Kinetic Energy (energy of motion) to potential gravitational energy (based off of height).
We can subtract 



so we can solve for the height
where
therefore
Compare your answer with the correct one above
If an object has a kinetic energy of  right after it is launched in the air, and it has
right after it is launched in the air, and it has  KE at its max height of
KE at its max height of  , what is the object's mass?
, what is the object's mass?
If an object has a kinetic energy of 


Let's first write down the information we are given:



In order to solve this problem we must apply the conservation of energy, which states  since no friction.
since no friction.
This means that as the project reaches its max height energy is converted from Kinetic energy (energy of motion) to potential gravitational energy (based off of height).
We can subtract  from
from  to get the
to get the  at its max height
at its max height
 =
=


so we can solve for the mass


where 
therefore 
Let's first write down the information we are given:
In order to solve this problem we must apply the conservation of energy, which states 
This means that as the project reaches its max height energy is converted from Kinetic energy (energy of motion) to potential gravitational energy (based off of height).
We can subtract 



so we can solve for the mass
where
therefore
Compare your answer with the correct one above
A baseball weighing  is dropped from a second story window which is
is dropped from a second story window which is  high. What is the gravitational potential energy?
high. What is the gravitational potential energy?

A baseball weighing 

Gravitational potential energy is given by the equation:

We are given all the information needed to solve for the potential energy.



Plug in known values and solve.



Recall that the units for energy are Joules. Newtons is the unit for force.
Gravitational potential energy is given by the equation:
We are given all the information needed to solve for the potential energy.
Plug in known values and solve.
Recall that the units for energy are Joules. Newtons is the unit for force.
Compare your answer with the correct one above
A  bowling ball is released from
bowling ball is released from  in the air. What is it's gravitation potential energy upon release?
in the air. What is it's gravitation potential energy upon release?

A 

The equation for gravitational potential energy is:

We are given all the information needed to answer the question.



Plug in known values and solve.


The equation for gravitational potential energy is:
We are given all the information needed to answer the question.
Plug in known values and solve.
Compare your answer with the correct one above
A pendulum on earth has a period of  . What is it's period on Mars with it's gravity is
. What is it's period on Mars with it's gravity is 
A pendulum on earth has a period of 
First, we need to find the length of the pendulum. Begin with the equation for finding the period of a pendulum:

solve for  to get:
to get:

Now we can plug in our given values:

Since we have the length of the pendulum determined, we can now find the period of the pendulum on Mars:

First, we need to find the length of the pendulum. Begin with the equation for finding the period of a pendulum:
solve for 
Now we can plug in our given values:
Since we have the length of the pendulum determined, we can now find the period of the pendulum on Mars:
Compare your answer with the correct one above
A  bouncy ball is dropped from
bouncy ball is dropped from  . When it bounces back up is reaches a height of
. When it bounces back up is reaches a height of  . How much energy was loss?
. How much energy was loss?

A 


The formula for gravitational potential energy is:

To find the potential energy lost, we need to find the potential energy of the ball at two heights, then find the difference.






Note that the energy was not actually lost; rather, it was converted to kinetic energy.
The formula for gravitational potential energy is:
To find the potential energy lost, we need to find the potential energy of the ball at two heights, then find the difference.
Note that the energy was not actually lost; rather, it was converted to kinetic energy.
Compare your answer with the correct one above
A car traveling at  has a kinetic energy
has a kinetic energy  . If the car accelerates to
. If the car accelerates to  , what will the new kinetic energy be?
, what will the new kinetic energy be?
A car traveling at 


Kinetic energy is given by . We will begin by calculating the car's initial kinetic energy, in terms of the unknown mass of the car
. We will begin by calculating the car's initial kinetic energy, in terms of the unknown mass of the car  :
:
 .
.
Next, we will calculate the final energy of the car, also in terms of the unknown mass of the car:
 .
.
To find the ratio of the final to initial kinetic energy, we divide  by
by  . We see that this reduces to
. We see that this reduces to  with the both the mass
with the both the mass  and
and  terms cancelling.
terms cancelling.  . Thus, the new kinetic energy is
. Thus, the new kinetic energy is  .
.
Kinetic energy is given by


Next, we will calculate the final energy of the car, also in terms of the unknown mass of the car:

To find the ratio of the final to initial kinetic energy, we divide 






Compare your answer with the correct one above
A  steel ball is in a spring loaded launcher. The spring has a constant of
steel ball is in a spring loaded launcher. The spring has a constant of  . If the ball is pulled back 50 cm then released and the ball leaves the launcher at a speed of
. If the ball is pulled back 50 cm then released and the ball leaves the launcher at a speed of  , how much work was done by friction?
, how much work was done by friction?
A 


So in order to solve this problem, we first should think about where all the energy in the system is coming from and going. Specifically when you pull the spring back, the work you do is turned into potential energy stored in the spring. So:

and the energy transforms into kinetic when you let go, but some of that energy is lost to friction so
 and
and 
So use the equation below, enter in your known quantities and then solve for the work done by friction.

Plug in known values and solve.


So in order to solve this problem, we first should think about where all the energy in the system is coming from and going. Specifically when you pull the spring back, the work you do is turned into potential energy stored in the spring. So:
and the energy transforms into kinetic when you let go, but some of that energy is lost to friction so

So use the equation below, enter in your known quantities and then solve for the work done by friction.
Plug in known values and solve.
Compare your answer with the correct one above
Suppose that an object of mass  is travelling towards a massless spring with a velocity
is travelling towards a massless spring with a velocity  . If the maximum displacement of the spring is
. If the maximum displacement of the spring is  , which of the following gives an expression for the spring constant,
, which of the following gives an expression for the spring constant, 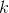 ?
?
Note: Assume that there is no friction.
Suppose that an object of mass 


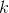
Note: Assume that there is no friction.
For this question, we're told than an object is travelling with a certain velocity towards a spring. After colliding with the spring and causing it to undergo a maximum displacement, we're asked to provide an expression for the spring constant.
In order to answer this question, we'll need to consider the energy of the object and the spring during the process described. First, the object is moving with a certain velocity towards the spring. Thus, the object has kinetic energy. When the object collides with the spring and displaces the spring to its maximum displacement, there will be a brief instant where the object has completely stopped moving. At this point, all of the block's kinetic energy will have been transferred into the spring in the form of potential energy. With this information in mind, we can equate the two forms of energy.

Now, we can rearrange terms in order to isolate  .
.

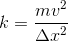
For this question, we're told than an object is travelling with a certain velocity towards a spring. After colliding with the spring and causing it to undergo a maximum displacement, we're asked to provide an expression for the spring constant.
In order to answer this question, we'll need to consider the energy of the object and the spring during the process described. First, the object is moving with a certain velocity towards the spring. Thus, the object has kinetic energy. When the object collides with the spring and displaces the spring to its maximum displacement, there will be a brief instant where the object has completely stopped moving. At this point, all of the block's kinetic energy will have been transferred into the spring in the form of potential energy. With this information in mind, we can equate the two forms of energy.
Now, we can rearrange terms in order to isolate 
Compare your answer with the correct one above
A pendulum is made up of a small  mass that hangs on the end of a
mass that hangs on the end of a  long string of negligible mass. The pendulum is displaced by
long string of negligible mass. The pendulum is displaced by  and allowed to undergo harmonic motion. What is the angular frequency of the resulting motion?
and allowed to undergo harmonic motion. What is the angular frequency of the resulting motion?

A pendulum is made up of a small 


The angular frequency of a simple pendulum is  , where
, where  is the length of the pendulum.
is the length of the pendulum.
The angular frequency of a simple pendulum is 

Compare your answer with the correct one above
For a simple harmonic motion governed by Hooke's Law,  , if
, if  is the period then the quantity
is the period then the quantity  is equivalent to which of the following?
is equivalent to which of the following?
For a simple harmonic motion governed by Hooke's Law, 


We know that T is the period. The equation for T is  for harmonic motion.
for harmonic motion.
Solve for  by dividing the equation by
by dividing the equation by  on both sides. The result is
on both sides. The result is  , which is the answer.
, which is the answer.
We know that T is the period. The equation for T is 
Solve for 


Compare your answer with the correct one above
If the mass of a simple pendulum is quadrupled, then its period .
If the mass of a simple pendulum is quadrupled, then its period .
We know that the equation for the period of a simple pendulum is  . This equation does not depend on mass. It is only affected by the length of the pendulum (L) and the gravitational constant (g). Therefore, adding mass to the pendulum will not effect the period, so the period remains the same.
. This equation does not depend on mass. It is only affected by the length of the pendulum (L) and the gravitational constant (g). Therefore, adding mass to the pendulum will not effect the period, so the period remains the same.
We know that the equation for the period of a simple pendulum is 
Compare your answer with the correct one above
A violin string  long has a linear density of
long has a linear density of  . What is the string tension if the second harmonic has a frequency of
. What is the string tension if the second harmonic has a frequency of  ?
?
A violin string 


Since we are solving for string tension, we need to use the frequency equation with the tension variable in it. That equation is  where
where  is the frequency,
is the frequency,  is the number of the harmonic,
is the number of the harmonic,  is the length of the string,
is the length of the string,  is the linear density of the string, and
is the linear density of the string, and  is the tension of the string.
is the tension of the string.
We are given:




Next we must convert the length of  to meters which is
to meters which is  and the mass density of
and the mass density of  to
to  . Then we plug in our known values into the equation and solve for the string tension. The result is
. Then we plug in our known values into the equation and solve for the string tension. The result is  .
.
Since we are solving for string tension, we need to use the frequency equation with the tension variable in it. That equation is 





We are given:
Next we must convert the length of 




Compare your answer with the correct one above
An hourglass is placed on a scale with all its sand in the upper chamber. A short time later, the sand begins to fall into the lower chamber. Which of the following best describes the reading on the scale as a function of time before any sand has accumulated in the bottom chamber?
An hourglass is placed on a scale with all its sand in the upper chamber. A short time later, the sand begins to fall into the lower chamber. Which of the following best describes the reading on the scale as a function of time before any sand has accumulated in the bottom chamber?
Initially, when all the sand is in the upper chamber, the reading on the scale is constant and corresponds to the weight of the hourglass and the sand within. As some sand falls, there is no normal force on it so the scale can not register its weight. The fraction of sand that is falling is small, so there is only a small decrease in the apparent weight of the hourglass.
Initially, when all the sand is in the upper chamber, the reading on the scale is constant and corresponds to the weight of the hourglass and the sand within. As some sand falls, there is no normal force on it so the scale can not register its weight. The fraction of sand that is falling is small, so there is only a small decrease in the apparent weight of the hourglass.
Compare your answer with the correct one above
Which of the following is not an example of simple harmonic motion?
Which of the following is not an example of simple harmonic motion?
For this question, we need to recall what simple harmonic motion is. Remember that it is a periodic motion where the restoring force depends on the displacement of the object undergoing these motions. So to answer this question, we need to keep this idea in mind and see which example doesn't match up.
A mass on a pendulum moving back and forth is clearly an example of simple harmonic motion. As the mass moves further from the center in either direction, it experiences a greater and greater force in the opposite direction.
A child swinging on a swing set is another correct example. This situation is analogous to the mass on a pendulum swinging back and forth.
A vibrating guitar string is yet another example of simple harmonic motion. After it is plucked, the string oscillates back and forth.
Finally, a book falling to the ground does not represent harmonic motion. Once the book is released from rest, we intuitively know that it will fall to the ground and will then stay there; in no way is there any periodic motion.
For this question, we need to recall what simple harmonic motion is. Remember that it is a periodic motion where the restoring force depends on the displacement of the object undergoing these motions. So to answer this question, we need to keep this idea in mind and see which example doesn't match up.
A mass on a pendulum moving back and forth is clearly an example of simple harmonic motion. As the mass moves further from the center in either direction, it experiences a greater and greater force in the opposite direction.
A child swinging on a swing set is another correct example. This situation is analogous to the mass on a pendulum swinging back and forth.
A vibrating guitar string is yet another example of simple harmonic motion. After it is plucked, the string oscillates back and forth.
Finally, a book falling to the ground does not represent harmonic motion. Once the book is released from rest, we intuitively know that it will fall to the ground and will then stay there; in no way is there any periodic motion.
Compare your answer with the correct one above
The bases on a baseball field are 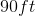 apart in a perfect square.
apart in a perfect square.
A player hits a home run and goes around all 4 bases. What is the total distance he travelled?
The bases on a baseball field are 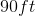
A player hits a home run and goes around all 4 bases. What is the total distance he travelled?
There is 90 feet between each base and distance does not depend on direction. Distance is scaler therefore, the batter travels 360 feet.
There is 90 feet between each base and distance does not depend on direction. Distance is scaler therefore, the batter travels 360 feet.
Compare your answer with the correct one above
The bases on a baseball field are  apart.
apart.
A player hits a home run and runs around all four bases. What is his total displacement?
The bases on a baseball field are 
A player hits a home run and runs around all four bases. What is his total displacement?
Displacement is a vector. Therefore, magnitude and direction matters and because direction matters the total displacement is 0 feet.
Displacement is a vector. Therefore, magnitude and direction matters and because direction matters the total displacement is 0 feet.
Compare your answer with the correct one above