Number Lines - Pre-Algebra
Card 0 of 32
Find the distance between  and
and  on a number line.
on a number line.
Find the distance between 

Tap to see back →
To find the distance on a number line:




To find the distance on a number line:
Plot the fraction  on the number line.
on the number line.
Plot the fraction 
Tap to see back →
The fraction  is less than
is less than 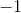 and greater than
and greater than  , so it must fall between those points on the number line. Negative numbers are to the left of
, so it must fall between those points on the number line. Negative numbers are to the left of  while positive numbers are to the right.
while positive numbers are to the right.

Because  is less than
is less than  , the point must be closer to
, the point must be closer to  than
than  .
.
The fraction 
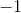


Because 



Which of the following numbers is depicted by the point on the number line?

Which of the following numbers is depicted by the point on the number line?

Tap to see back →
The point lies halfway between  and
and  , or at
, or at  .
.

The point lies halfway between 


Express this inequality statement using symbols.

Express this inequality statement using symbols.
Tap to see back →
 = less than
= less than
 = greater than
= greater than
 = less than or equal to
= less than or equal to
 = greater than or equal to
= greater than or equal to




Put in order from least to greatest.

Put in order from least to greatest.
Tap to see back →





Thus, in increasing order:

Thus, in increasing order:
Find the inequality that corresponds to the following number line.
Find the inequality that corresponds to the following number line.
Tap to see back →

When looking at the number line, we can see that x is any integer between 2 and 7.
Anything to the right of an integer is considered "greater than" and anything left of an integer is considered "less than".
So, we know that x is greater than 2, but less than 7.
Now, since the circle above the 2 is shaded in, 2 is included in the solution. The circle above the 7 is not shaded in, so 7 is not included in the solution.
We now know that x is greater than or equal to 2, and it is still less than 7.
Using the statement above, we will create 2 inequalities.


Now,  can also be written as
can also be written as  . It has the same value, it just looks a little different.
. It has the same value, it just looks a little different.
So we have the two inequalities
 and
and 
We can combine them, and it'll look like this

When looking at the number line, we can see that x is any integer between 2 and 7.
Anything to the right of an integer is considered "greater than" and anything left of an integer is considered "less than".
So, we know that x is greater than 2, but less than 7.
Now, since the circle above the 2 is shaded in, 2 is included in the solution. The circle above the 7 is not shaded in, so 7 is not included in the solution.
We now know that x is greater than or equal to 2, and it is still less than 7.
Using the statement above, we will create 2 inequalities.
Now, 

So we have the two inequalities

We can combine them, and it'll look like this
Find the inequality that corresponds with this number line.

Find the inequality that corresponds with this number line.
Tap to see back →
When looking at the number line,

we see at -5 there is a filled in circle. We also see there is an arrow going to the right of -5. Every integer to the right of -5 is greater than -5 itself. Because the circle above -5 is filled in, we know -5 is included in the inequality. We get

When looking at the number line,
we see at -5 there is a filled in circle. We also see there is an arrow going to the right of -5. Every integer to the right of -5 is greater than -5 itself. Because the circle above -5 is filled in, we know -5 is included in the inequality. We get
Put the following numbers in order from least to greatest.

Put the following numbers in order from least to greatest.
Tap to see back →
There is only one negative number in the numbers.

The next biggest is  ,
,

Next is  ,
,

Next is  ,
,

Lastly is 

There is only one negative number in the numbers.
The next biggest is 
Next is 
Next is 
Lastly is
Find the distance between  and
and  on a number line.
on a number line.
Find the distance between 

Tap to see back →
To find the distance on a number line:




To find the distance on a number line:
Plot the fraction  on the number line.
on the number line.
Plot the fraction 
Tap to see back →
The fraction  is less than
is less than 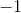 and greater than
and greater than  , so it must fall between those points on the number line. Negative numbers are to the left of
, so it must fall between those points on the number line. Negative numbers are to the left of  while positive numbers are to the right.
while positive numbers are to the right.

Because  is less than
is less than  , the point must be closer to
, the point must be closer to  than
than  .
.
The fraction 
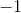


Because 



Which of the following numbers is depicted by the point on the number line?

Which of the following numbers is depicted by the point on the number line?

Tap to see back →
The point lies halfway between  and
and  , or at
, or at  .
.

The point lies halfway between 


Express this inequality statement using symbols.

Express this inequality statement using symbols.
Tap to see back →
 = less than
= less than
 = greater than
= greater than
 = less than or equal to
= less than or equal to
 = greater than or equal to
= greater than or equal to




Put in order from least to greatest.

Put in order from least to greatest.
Tap to see back →





Thus, in increasing order:

Thus, in increasing order:
Find the inequality that corresponds to the following number line.
Find the inequality that corresponds to the following number line.
Tap to see back →

When looking at the number line, we can see that x is any integer between 2 and 7.
Anything to the right of an integer is considered "greater than" and anything left of an integer is considered "less than".
So, we know that x is greater than 2, but less than 7.
Now, since the circle above the 2 is shaded in, 2 is included in the solution. The circle above the 7 is not shaded in, so 7 is not included in the solution.
We now know that x is greater than or equal to 2, and it is still less than 7.
Using the statement above, we will create 2 inequalities.


Now,  can also be written as
can also be written as  . It has the same value, it just looks a little different.
. It has the same value, it just looks a little different.
So we have the two inequalities
 and
and 
We can combine them, and it'll look like this

When looking at the number line, we can see that x is any integer between 2 and 7.
Anything to the right of an integer is considered "greater than" and anything left of an integer is considered "less than".
So, we know that x is greater than 2, but less than 7.
Now, since the circle above the 2 is shaded in, 2 is included in the solution. The circle above the 7 is not shaded in, so 7 is not included in the solution.
We now know that x is greater than or equal to 2, and it is still less than 7.
Using the statement above, we will create 2 inequalities.
Now, 

So we have the two inequalities

We can combine them, and it'll look like this
Find the inequality that corresponds with this number line.

Find the inequality that corresponds with this number line.
Tap to see back →
When looking at the number line,

we see at -5 there is a filled in circle. We also see there is an arrow going to the right of -5. Every integer to the right of -5 is greater than -5 itself. Because the circle above -5 is filled in, we know -5 is included in the inequality. We get

When looking at the number line,
we see at -5 there is a filled in circle. We also see there is an arrow going to the right of -5. Every integer to the right of -5 is greater than -5 itself. Because the circle above -5 is filled in, we know -5 is included in the inequality. We get
Put the following numbers in order from least to greatest.

Put the following numbers in order from least to greatest.
Tap to see back →
There is only one negative number in the numbers.

The next biggest is  ,
,

Next is  ,
,

Next is  ,
,

Lastly is 

There is only one negative number in the numbers.
The next biggest is 
Next is 
Next is 
Lastly is
Find the distance between  and
and  on a number line.
on a number line.
Find the distance between 

Tap to see back →
To find the distance on a number line:




To find the distance on a number line:
Plot the fraction  on the number line.
on the number line.
Plot the fraction 
Tap to see back →
The fraction  is less than
is less than 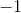 and greater than
and greater than  , so it must fall between those points on the number line. Negative numbers are to the left of
, so it must fall between those points on the number line. Negative numbers are to the left of  while positive numbers are to the right.
while positive numbers are to the right.

Because  is less than
is less than  , the point must be closer to
, the point must be closer to  than
than  .
.
The fraction 
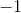


Because 



Which of the following numbers is depicted by the point on the number line?

Which of the following numbers is depicted by the point on the number line?

Tap to see back →
The point lies halfway between  and
and  , or at
, or at  .
.

The point lies halfway between 


Express this inequality statement using symbols.

Express this inequality statement using symbols.
Tap to see back →
 = less than
= less than
 = greater than
= greater than
 = less than or equal to
= less than or equal to
 = greater than or equal to
= greater than or equal to



