Find the Period of a Sine or Cosine Function - Pre-Calculus
Card 0 of 36
Please choose the best answer from the following choices.
Find the period of the following function in radians:

Please choose the best answer from the following choices.
Find the period of the following function in radians:
Tap to see back →
If you look at a graph, you can see that the period (length of one wave) is  . Without the graph, you can divide
. Without the graph, you can divide  with the frequency, which in this case, is 1.
with the frequency, which in this case, is 1.
If you look at a graph, you can see that the period (length of one wave) is 

Given  , what is the period for the function?
, what is the period for the function?
Given 
Tap to see back →
The formula for the period of a sine/cosine function is  .
.
With the standard form being:

Since  , the formula becomes
, the formula becomes  .
.
Simplified, the period is  .
.
The formula for the period of a sine/cosine function is 
With the standard form being:
Since 

Simplified, the period is 
What could be the function for the following graph?

What could be the function for the following graph?
Tap to see back →
What could be the function for the following graph?

Begin by realizing we are dealing with a periodic function, so sine and cosine are your best bet.
Next, note that the range of the function is  and that the function goes through the point
and that the function goes through the point  .
.
From this information, we can find the amplitude:

So our function must have a  out in front.
out in front.
Also, from the point  , we can deduce that the function has a vertical translation of positive two.
, we can deduce that the function has a vertical translation of positive two.
The only remaining obstacle, is whether the function is sine or cosine. Recall that sine passes through  , while cosine passes through
, while cosine passes through  . this means that our function must be a sine function, because in order to be a cosien graph, we would need a horizontal translation as well.
. this means that our function must be a sine function, because in order to be a cosien graph, we would need a horizontal translation as well.
Thus, our answer is:

What could be the function for the following graph?
Begin by realizing we are dealing with a periodic function, so sine and cosine are your best bet.
Next, note that the range of the function is 

From this information, we can find the amplitude:
So our function must have a 
Also, from the point 
The only remaining obstacle, is whether the function is sine or cosine. Recall that sine passes through 

Thus, our answer is:
What is the period of this sine graph?

What is the period of this sine graph?

Tap to see back →
The graph has 3 waves between 0 and  , meaning that the length of each of the waves is
, meaning that the length of each of the waves is  divided by 3, or
divided by 3, or  .
.
The graph has 3 waves between 0 and 


What is the period of this graph?

What is the period of this graph?

Tap to see back →
One wave of the graph goes exactly from 0 to  before repeating itself. This means that the period is
before repeating itself. This means that the period is  .
.
One wave of the graph goes exactly from 0 to 

Please choose the best answer from the following choices.
Find the period of the following function.

Please choose the best answer from the following choices.
Find the period of the following function.
Tap to see back →
The period is defined as the length of one wave of the function. In this case, one full wave is 180 degrees or  radians. You can figure this out without looking at a graph by dividing
radians. You can figure this out without looking at a graph by dividing  with the frequency, which in this case, is 2.
with the frequency, which in this case, is 2.
The period is defined as the length of one wave of the function. In this case, one full wave is 180 degrees or 

Write the equation for a cosine graph with a minimum at  and a maximum at
and a maximum at  .
.
Write the equation for a cosine graph with a minimum at 

Tap to see back →
The equation for this graph will be in the form  where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.
where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.
To write this equation, it is helpful to sketch a graph:
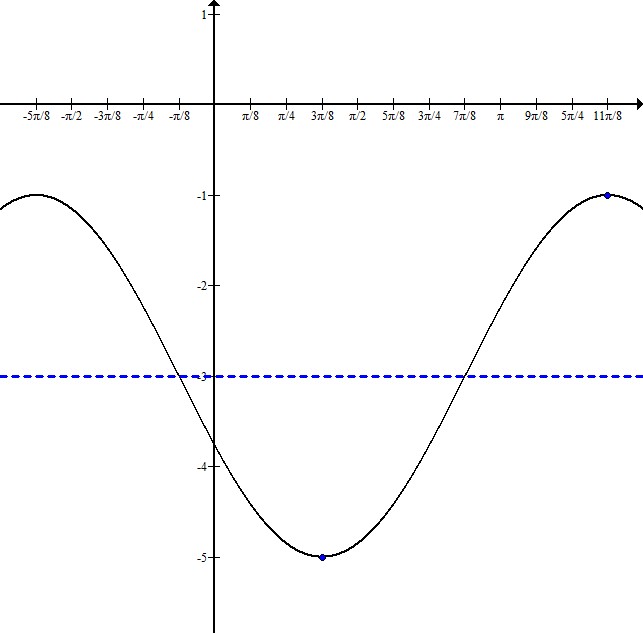
From sketching the maximum and the minimum, we can see that the graph is centered at  and has an amplitude of 2.
and has an amplitude of 2.
The distance between the maximum and the minimum is half the wavelength. Here, it is  . That means that the full wavelength is
. That means that the full wavelength is  , so the frequency is 1.
, so the frequency is 1.
The minimum occurs in the middle of the graph, so to figure out where it starts, subtract  from the minimum's x-coordinate:
from the minimum's x-coordinate:

This graph's equation is
 .
.
The equation for this graph will be in the form 
To write this equation, it is helpful to sketch a graph:

From sketching the maximum and the minimum, we can see that the graph is centered at 
The distance between the maximum and the minimum is half the wavelength. Here, it is 

The minimum occurs in the middle of the graph, so to figure out where it starts, subtract 
This graph's equation is

Give the period and frequency for the equation  .
.
Give the period and frequency for the equation 
Tap to see back →
Our equation is in the form 
where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.
We can look at the equation and see that the frequency,  , is
, is  .
.
The period is  , so in this case
, so in this case  .
.
Our equation is in the form
where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.
We can look at the equation and see that the frequency, 

The period is 

What is the period of the graph  ?
?
What is the period of the graph 
Tap to see back →
The equation for this function is in the form 
where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.
By looking at the equation, we can see that the frequency,  , is
, is  .
.
The period is  , so in this case
, so in this case  .
.
The equation for this function is in the form
where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.
By looking at the equation, we can see that the frequency, 

The period is 

Please choose the best answer from the following choices.
Find the period of the following function in radians:

Please choose the best answer from the following choices.
Find the period of the following function in radians:
Tap to see back →
If you look at a graph, you can see that the period (length of one wave) is  . Without the graph, you can divide
. Without the graph, you can divide  with the frequency, which in this case, is 1.
with the frequency, which in this case, is 1.
If you look at a graph, you can see that the period (length of one wave) is 

Given  , what is the period for the function?
, what is the period for the function?
Given 
Tap to see back →
The formula for the period of a sine/cosine function is  .
.
With the standard form being:

Since  , the formula becomes
, the formula becomes  .
.
Simplified, the period is  .
.
The formula for the period of a sine/cosine function is 
With the standard form being:
Since 

Simplified, the period is 
What could be the function for the following graph?

What could be the function for the following graph?
Tap to see back →
What could be the function for the following graph?

Begin by realizing we are dealing with a periodic function, so sine and cosine are your best bet.
Next, note that the range of the function is  and that the function goes through the point
and that the function goes through the point  .
.
From this information, we can find the amplitude:

So our function must have a  out in front.
out in front.
Also, from the point  , we can deduce that the function has a vertical translation of positive two.
, we can deduce that the function has a vertical translation of positive two.
The only remaining obstacle, is whether the function is sine or cosine. Recall that sine passes through  , while cosine passes through
, while cosine passes through  . this means that our function must be a sine function, because in order to be a cosien graph, we would need a horizontal translation as well.
. this means that our function must be a sine function, because in order to be a cosien graph, we would need a horizontal translation as well.
Thus, our answer is:

What could be the function for the following graph?
Begin by realizing we are dealing with a periodic function, so sine and cosine are your best bet.
Next, note that the range of the function is 

From this information, we can find the amplitude:
So our function must have a 
Also, from the point 
The only remaining obstacle, is whether the function is sine or cosine. Recall that sine passes through 

Thus, our answer is:
What is the period of this sine graph?

What is the period of this sine graph?

Tap to see back →
The graph has 3 waves between 0 and  , meaning that the length of each of the waves is
, meaning that the length of each of the waves is  divided by 3, or
divided by 3, or  .
.
The graph has 3 waves between 0 and 


What is the period of this graph?

What is the period of this graph?

Tap to see back →
One wave of the graph goes exactly from 0 to  before repeating itself. This means that the period is
before repeating itself. This means that the period is  .
.
One wave of the graph goes exactly from 0 to 

Please choose the best answer from the following choices.
Find the period of the following function.

Please choose the best answer from the following choices.
Find the period of the following function.
Tap to see back →
The period is defined as the length of one wave of the function. In this case, one full wave is 180 degrees or  radians. You can figure this out without looking at a graph by dividing
radians. You can figure this out without looking at a graph by dividing  with the frequency, which in this case, is 2.
with the frequency, which in this case, is 2.
The period is defined as the length of one wave of the function. In this case, one full wave is 180 degrees or 

Write the equation for a cosine graph with a minimum at  and a maximum at
and a maximum at  .
.
Write the equation for a cosine graph with a minimum at 

Tap to see back →
The equation for this graph will be in the form  where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.
where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.
To write this equation, it is helpful to sketch a graph:

From sketching the maximum and the minimum, we can see that the graph is centered at  and has an amplitude of 2.
and has an amplitude of 2.
The distance between the maximum and the minimum is half the wavelength. Here, it is  . That means that the full wavelength is
. That means that the full wavelength is  , so the frequency is 1.
, so the frequency is 1.
The minimum occurs in the middle of the graph, so to figure out where it starts, subtract  from the minimum's x-coordinate:
from the minimum's x-coordinate:

This graph's equation is
 .
.
The equation for this graph will be in the form 
To write this equation, it is helpful to sketch a graph:

From sketching the maximum and the minimum, we can see that the graph is centered at 
The distance between the maximum and the minimum is half the wavelength. Here, it is 

The minimum occurs in the middle of the graph, so to figure out where it starts, subtract 
This graph's equation is

Give the period and frequency for the equation  .
.
Give the period and frequency for the equation 
Tap to see back →
Our equation is in the form 
where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.
We can look at the equation and see that the frequency,  , is
, is  .
.
The period is  , so in this case
, so in this case  .
.
Our equation is in the form
where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.
We can look at the equation and see that the frequency, 

The period is 

What is the period of the graph  ?
?
What is the period of the graph 
Tap to see back →
The equation for this function is in the form 
where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.
By looking at the equation, we can see that the frequency,  , is
, is  .
.
The period is  , so in this case
, so in this case  .
.
The equation for this function is in the form
where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.
By looking at the equation, we can see that the frequency, 

The period is 

Given  , what is the period for the function?
, what is the period for the function?
Given 
Tap to see back →
The formula for the period of a sine/cosine function is  .
.
With the standard form being:

Since  , the formula becomes
, the formula becomes  .
.
Simplified, the period is  .
.
The formula for the period of a sine/cosine function is 
With the standard form being:
Since 

Simplified, the period is 
What could be the function for the following graph?

What could be the function for the following graph?
Tap to see back →
What could be the function for the following graph?

Begin by realizing we are dealing with a periodic function, so sine and cosine are your best bet.
Next, note that the range of the function is  and that the function goes through the point
and that the function goes through the point  .
.
From this information, we can find the amplitude:

So our function must have a  out in front.
out in front.
Also, from the point  , we can deduce that the function has a vertical translation of positive two.
, we can deduce that the function has a vertical translation of positive two.
The only remaining obstacle, is whether the function is sine or cosine. Recall that sine passes through  , while cosine passes through
, while cosine passes through  . this means that our function must be a sine function, because in order to be a cosien graph, we would need a horizontal translation as well.
. this means that our function must be a sine function, because in order to be a cosien graph, we would need a horizontal translation as well.
Thus, our answer is:

What could be the function for the following graph?
Begin by realizing we are dealing with a periodic function, so sine and cosine are your best bet.
Next, note that the range of the function is 

From this information, we can find the amplitude:
So our function must have a 
Also, from the point 
The only remaining obstacle, is whether the function is sine or cosine. Recall that sine passes through 

Thus, our answer is: