Functions - Pre-Calculus
Card 0 of 644
Add the following functions:

Add the following functions:
Tap to see back →
To add, simply combine like terms. Thus, the answer is:

To add, simply combine like terms. Thus, the answer is:
Find the inverse of the following equation:

Find the inverse of the following equation:
Tap to see back →
To find the inverse of a function, replace the x any y positions:
Original Equation: 
Inversed Equation: 
Now solve for the inversed y value.





To find the inverse of a function, replace the x any y positions:
Original Equation:
Inversed Equation:
Now solve for the inversed y value.
What is the inverse function of
 ?
?
What is the inverse function of

Tap to see back →
To find the inverse function of

we replace the  with
with  and vice versa.
and vice versa.
So

Now solve for 




To find the inverse function of
we replace the 

So
Now solve for
Evaluate: 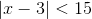
Evaluate:
Tap to see back →
Cancel the absolute value sign by separating the function  into its positive and negative counterparts.
into its positive and negative counterparts.


Evaluate the first scenario.


Evaluate the second scenario.



The correct answer is:

Cancel the absolute value sign by separating the function 
Evaluate the first scenario.
Evaluate the second scenario.
The correct answer is:
Which of the following is a point on the following function?

Which of the following is a point on the following function?
Tap to see back →
One way to approach this problem would be to plug in each answer and see what works. However, I would be a little more strategic and eliminate any options that don't make sense.
Our y value will never be negative, so eliminate any options with a negative y-value.
Try (0,0) really quick, since it's really easy

The only point that makes sense is (5,83), therefore it is the correct answer

One way to approach this problem would be to plug in each answer and see what works. However, I would be a little more strategic and eliminate any options that don't make sense.
Our y value will never be negative, so eliminate any options with a negative y-value.
Try (0,0) really quick, since it's really easy
The only point that makes sense is (5,83), therefore it is the correct answer
If  , then what is the value of
, then what is the value of  when
when 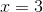 ?
?
If 

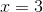
Tap to see back →
We evaluate for 



Since the absolute value of any number represents its magnitude from  and is therefore always positive, the final answer would be
and is therefore always positive, the final answer would be 
We evaluate for
Since the absolute value of any number represents its magnitude from 
If  is the greatest integer function, what is the value of
is the greatest integer function, what is the value of  ?
?
If 

Tap to see back →
The greatest integer function takes an input and produces the greatest integer less than the input. Thus, the output is always smaller than the input and is an integer itself. Since our input was  , we are looking for an integer less than this, which must be
, we are looking for an integer less than this, which must be  since any smaller integer would by definition not be "greatest".
since any smaller integer would by definition not be "greatest".
The greatest integer function takes an input and produces the greatest integer less than the input. Thus, the output is always smaller than the input and is an integer itself. Since our input was 

Which of the following expressions is not a function?
Which of the following expressions is not a function?
Tap to see back →
Recall that an expression is only a function if it passes the vertical line test. Test this by graphing each function and looking for one which fails the vertical line test. (The vertical line test consists of drawing a vertical line through the graph of an expression. If the vertical line crosses the graph of the expression more than once, the expression is not a function.)
Functions can only have one y value for every x value. The only choice that reflects this is:

Recall that an expression is only a function if it passes the vertical line test. Test this by graphing each function and looking for one which fails the vertical line test. (The vertical line test consists of drawing a vertical line through the graph of an expression. If the vertical line crosses the graph of the expression more than once, the expression is not a function.)
Functions can only have one y value for every x value. The only choice that reflects this is:
Suppose we have the relation  on the set of real numbers
on the set of real numbers  whenever
whenever  . Which of the following is true.
. Which of the following is true.
Suppose we have the relation 


Tap to see back →
The relation is not a function because  and
and  hold. If it were a function,
hold. If it were a function,  would hold only for one
would hold only for one  . But we know it holds for
. But we know it holds for  because
because  and
and  . Thus, the relation
. Thus, the relation  on the set of real numbers
on the set of real numbers  is not a function.
is not a function.
The relation is not a function because 








Consider a family consisting of a two parents, Juan and Oksana, and their daughters Adriana and Laksmi. A relation  is true whenever
is true whenever  is the child of
is the child of  . Which of the following is not true?
. Which of the following is not true?
Consider a family consisting of a two parents, Juan and Oksana, and their daughters Adriana and Laksmi. A relation 


Tap to see back →
The statement
"Even if the two parents had only one daughter, the relation would not be a function."
is not true because if they had only one daughter, say Adriana, then the only relations that would exist would be (Juan, Adriana) and (Oksana,Adriana), which defines a function.
The statement
"Even if the two parents had only one daughter, the relation would not be a function."
is not true because if they had only one daughter, say Adriana, then the only relations that would exist would be (Juan, Adriana) and (Oksana,Adriana), which defines a function.
Which of the following relations is not a function?
Which of the following relations is not a function?
Tap to see back →
The definition of a function requires that for each input (i.e. each value of  ), there is only one output (i.e. one value of
), there is only one output (i.e. one value of  ). For
). For  , each value of
, each value of  corresponds to two values of
corresponds to two values of  (for example, when
(for example, when  , both
, both  and
and  are correct solutions). Therefore, this relation cannot be a function.
are correct solutions). Therefore, this relation cannot be a function.
The definition of a function requires that for each input (i.e. each value of 







Given the set of ordered pairs, determine if the relation is a function





Given the set of ordered pairs, determine if the relation is a function
Tap to see back →
A relation is a function if no single x-value corresponds to more than one y-value.
Because the mapping from  goes to
goes to  and
and 
the relation is NOT a function.
A relation is a function if no single x-value corresponds to more than one y-value.
Because the mapping from 

the relation is NOT a function.
What equation is perpendicular to  and passes throgh
and passes throgh  ?
?
What equation is perpendicular to 

Tap to see back →
First find the reciprocal of the slope of the given function.


The perpendicular function is:

Now we must find the constant,  , by using the given point that the perpendicular crosses.
, by using the given point that the perpendicular crosses.

solve for  :
:


First find the reciprocal of the slope of the given function.
The perpendicular function is:
Now we must find the constant, 
solve for 
Is the following relation of ordered pairs a function?

Is the following relation of ordered pairs a function?
Tap to see back →
A set of ordered pairs is a function if it passes the vertical line test.
Because there are no more than one corresponding  value for any given
value for any given  value, the relation of ordered pairs IS a function.
value, the relation of ordered pairs IS a function.
A set of ordered pairs is a function if it passes the vertical line test.
Because there are no more than one corresponding 

Find the range of the following function:

Find the range of the following function:
Tap to see back →
Every element of the domain has as image 7.This means that the function is constant . Therefore,
the range of f is :{7}.
Every element of the domain has as image 7.This means that the function is constant . Therefore,
the range of f is :{7}.
What is the range of  :
:

What is the range of 
Tap to see back →
We know that  . So
. So  .
.
Therefore:
 .
.
This gives:
 .
.
Therefore the range is:
![[-1,3]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/250357/gif.latex)
We know that 

Therefore:

This gives:

Therefore the range is:
Find the range of f(x) given below:

Find the range of f(x) given below:
Tap to see back →
Note that: we can write f(x) as :
 .
.
Since,

Therefore,

So the range is 
Note that: we can write f(x) as :

Since,
Therefore,
So the range is
What is the range of  :
:

What is the range of 
Tap to see back →
We have  .
.
Adding 7 to both sides we have:
 .
.
Therefore  .
.
This means that the range of f is ![[6,8]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/250369/gif.latex)
We have 
Adding 7 to both sides we have:

Therefore 
This means that the range of f is
Find the domain of the following function:

Find the domain of the following function:
Tap to see back →
The part inside the square root must be positive. This means that we must be  . Thus
. Thus
 . Adding -121 to both sides gives
. Adding -121 to both sides gives  . Finally multiplying both sides by (-1) give:
. Finally multiplying both sides by (-1) give:
 with x reals. This gives the answer.
with x reals. This gives the answer.
Note: When we divide by a negative we need to flip our sign.
The part inside the square root must be positive. This means that we must be 



Note: When we divide by a negative we need to flip our sign.
What is the domain of the function given by:

What is the domain of the function given by:
Tap to see back →
cos(x) is definded for all reals. cos(x) is always between -1 and 1. Thus  . The value inside the square is always positive. Therefore the domain is the set of all real numbers.
. The value inside the square is always positive. Therefore the domain is the set of all real numbers.
cos(x) is definded for all reals. cos(x) is always between -1 and 1. Thus 