Special Functions - Pre-Calculus
Card 0 of 36
Evaluate: 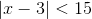
Evaluate:
Tap to see back →
Cancel the absolute value sign by separating the function  into its positive and negative counterparts.
into its positive and negative counterparts.


Evaluate the first scenario.


Evaluate the second scenario.



The correct answer is:

Cancel the absolute value sign by separating the function 
Evaluate the first scenario.
Evaluate the second scenario.
The correct answer is:
Which of the following is a point on the following function?

Which of the following is a point on the following function?
Tap to see back →
One way to approach this problem would be to plug in each answer and see what works. However, I would be a little more strategic and eliminate any options that don't make sense.
Our y value will never be negative, so eliminate any options with a negative y-value.
Try (0,0) really quick, since it's really easy

The only point that makes sense is (5,83), therefore it is the correct answer

One way to approach this problem would be to plug in each answer and see what works. However, I would be a little more strategic and eliminate any options that don't make sense.
Our y value will never be negative, so eliminate any options with a negative y-value.
Try (0,0) really quick, since it's really easy
The only point that makes sense is (5,83), therefore it is the correct answer
If  , then what is the value of
, then what is the value of  when
when 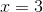 ?
?
If 

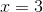
Tap to see back →
We evaluate for 



Since the absolute value of any number represents its magnitude from  and is therefore always positive, the final answer would be
and is therefore always positive, the final answer would be 
We evaluate for
Since the absolute value of any number represents its magnitude from 
If  is the greatest integer function, what is the value of
is the greatest integer function, what is the value of  ?
?
If 

Tap to see back →
The greatest integer function takes an input and produces the greatest integer less than the input. Thus, the output is always smaller than the input and is an integer itself. Since our input was  , we are looking for an integer less than this, which must be
, we are looking for an integer less than this, which must be  since any smaller integer would by definition not be "greatest".
since any smaller integer would by definition not be "greatest".
The greatest integer function takes an input and produces the greatest integer less than the input. Thus, the output is always smaller than the input and is an integer itself. Since our input was 

Evaluate: 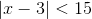
Evaluate:
Tap to see back →
Cancel the absolute value sign by separating the function  into its positive and negative counterparts.
into its positive and negative counterparts.


Evaluate the first scenario.


Evaluate the second scenario.



The correct answer is:

Cancel the absolute value sign by separating the function 
Evaluate the first scenario.
Evaluate the second scenario.
The correct answer is:
Which of the following is a point on the following function?

Which of the following is a point on the following function?
Tap to see back →
One way to approach this problem would be to plug in each answer and see what works. However, I would be a little more strategic and eliminate any options that don't make sense.
Our y value will never be negative, so eliminate any options with a negative y-value.
Try (0,0) really quick, since it's really easy

The only point that makes sense is (5,83), therefore it is the correct answer

One way to approach this problem would be to plug in each answer and see what works. However, I would be a little more strategic and eliminate any options that don't make sense.
Our y value will never be negative, so eliminate any options with a negative y-value.
Try (0,0) really quick, since it's really easy
The only point that makes sense is (5,83), therefore it is the correct answer
If  , then what is the value of
, then what is the value of  when
when 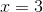 ?
?
If 

Tap to see back →
We evaluate for 



Since the absolute value of any number represents its magnitude from  and is therefore always positive, the final answer would be
and is therefore always positive, the final answer would be 
We evaluate for
Since the absolute value of any number represents its magnitude from 
If  is the greatest integer function, what is the value of
is the greatest integer function, what is the value of  ?
?
If 

Tap to see back →
The greatest integer function takes an input and produces the greatest integer less than the input. Thus, the output is always smaller than the input and is an integer itself. Since our input was  , we are looking for an integer less than this, which must be
, we are looking for an integer less than this, which must be  since any smaller integer would by definition not be "greatest".
since any smaller integer would by definition not be "greatest".
The greatest integer function takes an input and produces the greatest integer less than the input. Thus, the output is always smaller than the input and is an integer itself. Since our input was 

Which of the following is a point on the following function?

Which of the following is a point on the following function?
Tap to see back →
One way to approach this problem would be to plug in each answer and see what works. However, I would be a little more strategic and eliminate any options that don't make sense.
Our y value will never be negative, so eliminate any options with a negative y-value.
Try (0,0) really quick, since it's really easy

The only point that makes sense is (5,83), therefore it is the correct answer

One way to approach this problem would be to plug in each answer and see what works. However, I would be a little more strategic and eliminate any options that don't make sense.
Our y value will never be negative, so eliminate any options with a negative y-value.
Try (0,0) really quick, since it's really easy
The only point that makes sense is (5,83), therefore it is the correct answer
Evaluate: 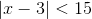
Evaluate:
Tap to see back →
Cancel the absolute value sign by separating the function  into its positive and negative counterparts.
into its positive and negative counterparts.


Evaluate the first scenario.


Evaluate the second scenario.



The correct answer is:

Cancel the absolute value sign by separating the function 
Evaluate the first scenario.
Evaluate the second scenario.
The correct answer is:
If  , then what is the value of
, then what is the value of  when
when 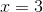 ?
?
If 

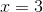
Tap to see back →
We evaluate for 



Since the absolute value of any number represents its magnitude from  and is therefore always positive, the final answer would be
and is therefore always positive, the final answer would be 
We evaluate for
Since the absolute value of any number represents its magnitude from 
If  is the greatest integer function, what is the value of
is the greatest integer function, what is the value of  ?
?
If 

Tap to see back →
The greatest integer function takes an input and produces the greatest integer less than the input. Thus, the output is always smaller than the input and is an integer itself. Since our input was  , we are looking for an integer less than this, which must be
, we are looking for an integer less than this, which must be  since any smaller integer would by definition not be "greatest".
since any smaller integer would by definition not be "greatest".
The greatest integer function takes an input and produces the greatest integer less than the input. Thus, the output is always smaller than the input and is an integer itself. Since our input was 

Which of the following is a point on the following function?

Which of the following is a point on the following function?
Tap to see back →
One way to approach this problem would be to plug in each answer and see what works. However, I would be a little more strategic and eliminate any options that don't make sense.
Our y value will never be negative, so eliminate any options with a negative y-value.
Try (0,0) really quick, since it's really easy

The only point that makes sense is (5,83), therefore it is the correct answer

One way to approach this problem would be to plug in each answer and see what works. However, I would be a little more strategic and eliminate any options that don't make sense.
Our y value will never be negative, so eliminate any options with a negative y-value.
Try (0,0) really quick, since it's really easy
The only point that makes sense is (5,83), therefore it is the correct answer
Evaluate: 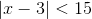
Evaluate:
Tap to see back →
Cancel the absolute value sign by separating the function  into its positive and negative counterparts.
into its positive and negative counterparts.


Evaluate the first scenario.


Evaluate the second scenario.



The correct answer is:

Cancel the absolute value sign by separating the function 
Evaluate the first scenario.
Evaluate the second scenario.
The correct answer is:
If  , then what is the value of
, then what is the value of  when
when 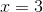 ?
?
If 

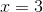
Tap to see back →
We evaluate for 



Since the absolute value of any number represents its magnitude from  and is therefore always positive, the final answer would be
and is therefore always positive, the final answer would be 
We evaluate for
Since the absolute value of any number represents its magnitude from 
If  is the greatest integer function, what is the value of
is the greatest integer function, what is the value of  ?
?
If 

Tap to see back →
The greatest integer function takes an input and produces the greatest integer less than the input. Thus, the output is always smaller than the input and is an integer itself. Since our input was  , we are looking for an integer less than this, which must be
, we are looking for an integer less than this, which must be  since any smaller integer would by definition not be "greatest".
since any smaller integer would by definition not be "greatest".
The greatest integer function takes an input and produces the greatest integer less than the input. Thus, the output is always smaller than the input and is an integer itself. Since our input was 

For the function  defined below, what is the value of
defined below, what is the value of  when
when  ?
?

For the function 


Tap to see back →
Evaluate the function for  . Based on the domains of the three given expressions, you would use
. Based on the domains of the three given expressions, you would use  , since
, since  is greater than or equal to
is greater than or equal to  .
.

Evaluate the function for 



For the function  defined below, what is the value of
defined below, what is the value of  when
when  ?
?

For the function 


Tap to see back →
Evaluate the function for  . Based on the domains of the three given expressions, you would use
. Based on the domains of the three given expressions, you would use  , since
, since  is greater than or equal to
is greater than or equal to  .
.

Evaluate the function for 



Let

What does  equal when
equal when  ?
?
Let
What does 

Tap to see back →
Because 3>0 we plug the x value into the bottom equation.



Because 3>0 we plug the x value into the bottom equation.
Let

What does  equal when
equal when  ?
?
Let
What does 

Tap to see back →
Because 3>0 we plug the x value into the bottom equation.



Because 3>0 we plug the x value into the bottom equation.

