Set Up an Equation That Models Harmonic Motion - Pre-Calculus
Card 0 of 4
Create an equation modelling temperature  , with highest temperature at
, with highest temperature at  , which is
, which is 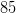 degrees and lowest temperature of
degrees and lowest temperature of  degrees which occurs at
degrees which occurs at  . Assume that this model is sinusoidal and use a cosine model.
. Assume that this model is sinusoidal and use a cosine model.
Create an equation modelling temperature 



Tap to see back →
This can be written in the general form of:
 .
.
Since the maximum occurs at  , we can arbitrarily choose
, we can arbitrarily choose  since cosine would be maximum when the inner term is equal to
since cosine would be maximum when the inner term is equal to  .
.
To determine  , let's determine the period first.
, let's determine the period first.
The period is equal to twice the length between adjacent crest and trough.
For us that is:
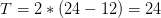
To determine  , we do
, we do

To determine 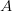 ,
,

To determine  ,
,

The entire regression can therefore be written as:

The only thing that can be changed to keep the regression the same is the phase shift  , and sign of the amplitude
, and sign of the amplitude  . The other two terms must be kept as they are.
. The other two terms must be kept as they are.
This can be written in the general form of:

Since the maximum occurs at 


To determine 
The period is equal to twice the length between adjacent crest and trough.
For us that is:
To determine 
To determine 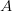
To determine 
The entire regression can therefore be written as:
The only thing that can be changed to keep the regression the same is the phase shift 

Create an equation modelling temperature  , with highest temperature at
, with highest temperature at  , which is
, which is 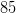 degrees and lowest temperature of
degrees and lowest temperature of  degrees which occurs at
degrees which occurs at  . Assume that this model is sinusoidal and use a cosine model.
. Assume that this model is sinusoidal and use a cosine model.
Create an equation modelling temperature 

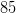


Tap to see back →
This can be written in the general form of:
 .
.
Since the maximum occurs at  , we can arbitrarily choose
, we can arbitrarily choose  since cosine would be maximum when the inner term is equal to
since cosine would be maximum when the inner term is equal to  .
.
To determine  , let's determine the period first.
, let's determine the period first.
The period is equal to twice the length between adjacent crest and trough.
For us that is:
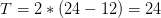
To determine  , we do
, we do

To determine 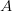 ,
,

To determine  ,
,

The entire regression can therefore be written as:

The only thing that can be changed to keep the regression the same is the phase shift  , and sign of the amplitude
, and sign of the amplitude  . The other two terms must be kept as they are.
. The other two terms must be kept as they are.
This can be written in the general form of:

Since the maximum occurs at 


To determine 
The period is equal to twice the length between adjacent crest and trough.
For us that is:
To determine 
To determine 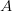
To determine 
The entire regression can therefore be written as:
The only thing that can be changed to keep the regression the same is the phase shift 

Create an equation modelling temperature  , with highest temperature at
, with highest temperature at  , which is
, which is 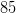 degrees and lowest temperature of
degrees and lowest temperature of  degrees which occurs at
degrees which occurs at  . Assume that this model is sinusoidal and use a cosine model.
. Assume that this model is sinusoidal and use a cosine model.
Create an equation modelling temperature 

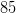


Tap to see back →
This can be written in the general form of:
 .
.
Since the maximum occurs at  , we can arbitrarily choose
, we can arbitrarily choose  since cosine would be maximum when the inner term is equal to
since cosine would be maximum when the inner term is equal to  .
.
To determine  , let's determine the period first.
, let's determine the period first.
The period is equal to twice the length between adjacent crest and trough.
For us that is:
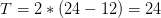
To determine  , we do
, we do

To determine 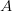 ,
,

To determine  ,
,

The entire regression can therefore be written as:

The only thing that can be changed to keep the regression the same is the phase shift  , and sign of the amplitude
, and sign of the amplitude  . The other two terms must be kept as they are.
. The other two terms must be kept as they are.
This can be written in the general form of:

Since the maximum occurs at 


To determine 
The period is equal to twice the length between adjacent crest and trough.
For us that is:
To determine 
To determine 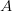
To determine 
The entire regression can therefore be written as:
The only thing that can be changed to keep the regression the same is the phase shift 

Create an equation modelling temperature  , with highest temperature at
, with highest temperature at  , which is
, which is 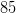 degrees and lowest temperature of
degrees and lowest temperature of  degrees which occurs at
degrees which occurs at  . Assume that this model is sinusoidal and use a cosine model.
. Assume that this model is sinusoidal and use a cosine model.
Create an equation modelling temperature 

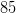


Tap to see back →
This can be written in the general form of:
 .
.
Since the maximum occurs at  , we can arbitrarily choose
, we can arbitrarily choose  since cosine would be maximum when the inner term is equal to
since cosine would be maximum when the inner term is equal to  .
.
To determine  , let's determine the period first.
, let's determine the period first.
The period is equal to twice the length between adjacent crest and trough.
For us that is:
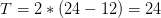
To determine  , we do
, we do

To determine 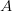 ,
,

To determine  ,
,

The entire regression can therefore be written as:

The only thing that can be changed to keep the regression the same is the phase shift  , and sign of the amplitude
, and sign of the amplitude  . The other two terms must be kept as they are.
. The other two terms must be kept as they are.
This can be written in the general form of:

Since the maximum occurs at 


To determine 
The period is equal to twice the length between adjacent crest and trough.
For us that is:
To determine 
To determine 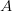
To determine 
The entire regression can therefore be written as:
The only thing that can be changed to keep the regression the same is the phase shift 
