Write the Equation of a Polynomial Function Based on Its Graph - Pre-Calculus
Card 0 of 28
Which could be the equation for this graph?

Which could be the equation for this graph?
Tap to see back →
This graph has zeros at 3, -2, and -4.5. This means that  ,
,  , and
, and  . That last root is easier to work with if we consider it as
. That last root is easier to work with if we consider it as  and simplify it to
and simplify it to  . Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.
. Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.
Our equation results from multiplying  , which results in
, which results in  .
.
This graph has zeros at 3, -2, and -4.5. This means that 




Our equation results from multiplying 

Write the quadratic function for the graph:

Write the quadratic function for the graph:

Tap to see back →
Method 1:
The x-intercepts are  . These values would be obtained if the original quadratic were factored, or reverse-FOILed and the factors were set equal to zero.
. These values would be obtained if the original quadratic were factored, or reverse-FOILed and the factors were set equal to zero.
For  ,
,  . For
. For  ,
,  . These equations determine the resulting factors and the resulting function;
. These equations determine the resulting factors and the resulting function;  .
.
Multiplying the factors and simplifying,
 .
.
Answer:  .
.
Method 2:
Use the form  , where
, where  is the vertex.
is the vertex.
 is
is  , so
, so  ,
,  .
.
![(x - $[-4])^{2}$ + (-4) = (x + $4)^{2}$ - 4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/478227/gif.latex)
Answer: 



Method 1:
The x-intercepts are 
For 




Multiplying the factors and simplifying,

Answer: 
Method 2:
Use the form 





Answer:
Write the quadratic function for the graph:

Write the quadratic function for the graph:

Tap to see back →
Because there are no x-intercepts, use the form  , where vertex
, where vertex  is
is  , so
, so  ,
,  , which gives
, which gives





Because there are no x-intercepts, use the form 




Write the equation for the polynomial in this graph:
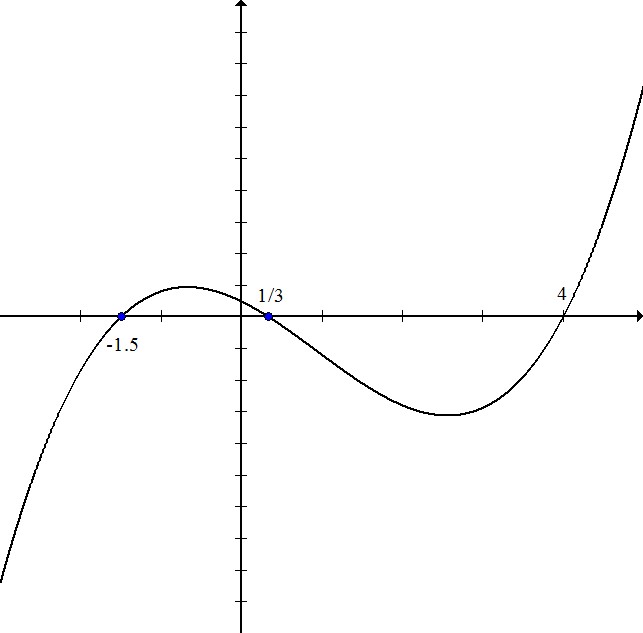
Write the equation for the polynomial in this graph:

Tap to see back →
The zeros for this polynomial are  .
.
This means that the factors are equal to zero when these values are plugged in for x.
 multiply both sides by 2
multiply both sides by 2
 so one factor is
so one factor is 
 multiply both sides by 3
multiply both sides by 3
 so one factor is
so one factor is 
 so one factor is
so one factor is 
Multiply these three factors:



The zeros for this polynomial are 
This means that the factors are equal to zero when these values are plugged in for x.





Multiply these three factors:
Write the equation for the polynomial shown in this graph:

Write the equation for the polynomial shown in this graph:

Tap to see back →
The zeros of this polynomial are  . This means that the factors equal zero when these values are plugged in.
. This means that the factors equal zero when these values are plugged in.
One factor is 
One factor is 
The third factor is equivalent to  . Set equal to 0 and multiply by 2:
. Set equal to 0 and multiply by 2:


Multiply these three factors:


The graph is negative since it goes down then up then down, so we have to switch all of the signs:

The zeros of this polynomial are 
One factor is
One factor is
The third factor is equivalent to 
Multiply these three factors:
The graph is negative since it goes down then up then down, so we have to switch all of the signs:
Write the equation for the polynomial in this graph:

Write the equation for the polynomial in this graph:

Tap to see back →
The zeros for this polynomial are  . That means that the factors are equal to zero when these values are plugged in.
. That means that the factors are equal to zero when these values are plugged in.
 or equivalently
or equivalently  multiply both sides by 4
multiply both sides by 4
 the first factor is
the first factor is 
 multiply both sides by 3
multiply both sides by 3
 the second factor is
the second factor is 
 the third factor is
the third factor is 
Multiply the three factors:



The zeros for this polynomial are 






Multiply the three factors:
Write the equation for the polynomial in the graph:
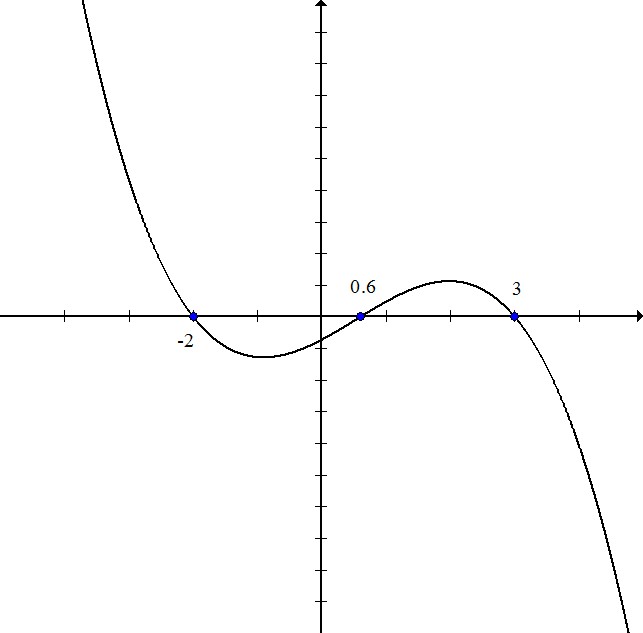
Write the equation for the polynomial in the graph:

Tap to see back →
The zeros of the polynomial are  . That means that the factors equal zero when these values are plugged in.
. That means that the factors equal zero when these values are plugged in.
The first factor is  or equivalently
or equivalently  multiply both sides by 5:
multiply both sides by 5:

The second and third factors are  and
and 
Multiply:



Because the graph goes down-up-down instead of the standard up-down-up, the graph is negative, so change all of the signs:

The zeros of the polynomial are 
The first factor is 

The second and third factors are 
Multiply:
Because the graph goes down-up-down instead of the standard up-down-up, the graph is negative, so change all of the signs:
Which could be the equation for this graph?

Which could be the equation for this graph?
Tap to see back →
This graph has zeros at 3, -2, and -4.5. This means that  ,
,  , and
, and  . That last root is easier to work with if we consider it as
. That last root is easier to work with if we consider it as  and simplify it to
and simplify it to  . Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.
. Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.
Our equation results from multiplying  , which results in
, which results in  .
.
This graph has zeros at 3, -2, and -4.5. This means that 




Our equation results from multiplying 

Write the quadratic function for the graph:

Write the quadratic function for the graph:

Tap to see back →
Method 1:
The x-intercepts are  . These values would be obtained if the original quadratic were factored, or reverse-FOILed and the factors were set equal to zero.
. These values would be obtained if the original quadratic were factored, or reverse-FOILed and the factors were set equal to zero.
For  ,
,  . For
. For  ,
,  . These equations determine the resulting factors and the resulting function;
. These equations determine the resulting factors and the resulting function;  .
.
Multiplying the factors and simplifying,
 .
.
Answer:  .
.
Method 2:
Use the form  , where
, where  is the vertex.
is the vertex.
 is
is  , so
, so  ,
,  .
.
![(x - $[-4])^{2}$ + (-4) = (x + $4)^{2}$ - 4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/478227/gif.latex)
Answer: 



Method 1:
The x-intercepts are 
For 




Multiplying the factors and simplifying,

Answer: 
Method 2:
Use the form 





Answer:
Write the quadratic function for the graph:

Write the quadratic function for the graph:

Tap to see back →
Because there are no x-intercepts, use the form  , where vertex
, where vertex  is
is  , so
, so  ,
,  , which gives
, which gives





Because there are no x-intercepts, use the form 




Write the equation for the polynomial in this graph:

Write the equation for the polynomial in this graph:

Tap to see back →
The zeros for this polynomial are  .
.
This means that the factors are equal to zero when these values are plugged in for x.
 multiply both sides by 2
multiply both sides by 2
 so one factor is
so one factor is 
 multiply both sides by 3
multiply both sides by 3
 so one factor is
so one factor is 
 so one factor is
so one factor is 
Multiply these three factors:



The zeros for this polynomial are 
This means that the factors are equal to zero when these values are plugged in for x.





Multiply these three factors:
Write the equation for the polynomial shown in this graph:

Write the equation for the polynomial shown in this graph:

Tap to see back →
The zeros of this polynomial are  . This means that the factors equal zero when these values are plugged in.
. This means that the factors equal zero when these values are plugged in.
One factor is 
One factor is 
The third factor is equivalent to  . Set equal to 0 and multiply by 2:
. Set equal to 0 and multiply by 2:


Multiply these three factors:


The graph is negative since it goes down then up then down, so we have to switch all of the signs:

The zeros of this polynomial are 
One factor is
One factor is
The third factor is equivalent to 
Multiply these three factors:
The graph is negative since it goes down then up then down, so we have to switch all of the signs:
Write the equation for the polynomial in this graph:

Write the equation for the polynomial in this graph:

Tap to see back →
The zeros for this polynomial are  . That means that the factors are equal to zero when these values are plugged in.
. That means that the factors are equal to zero when these values are plugged in.
 or equivalently
or equivalently  multiply both sides by 4
multiply both sides by 4
 the first factor is
the first factor is 
 multiply both sides by 3
multiply both sides by 3
 the second factor is
the second factor is 
 the third factor is
the third factor is 
Multiply the three factors:



The zeros for this polynomial are 






Multiply the three factors:
Write the equation for the polynomial in the graph:

Write the equation for the polynomial in the graph:

Tap to see back →
The zeros of the polynomial are  . That means that the factors equal zero when these values are plugged in.
. That means that the factors equal zero when these values are plugged in.
The first factor is  or equivalently
or equivalently  multiply both sides by 5:
multiply both sides by 5:

The second and third factors are  and
and 
Multiply:



Because the graph goes down-up-down instead of the standard up-down-up, the graph is negative, so change all of the signs:

The zeros of the polynomial are 
The first factor is 

The second and third factors are 
Multiply:
Because the graph goes down-up-down instead of the standard up-down-up, the graph is negative, so change all of the signs:
Write the quadratic function for the graph:

Write the quadratic function for the graph:

Tap to see back →
Method 1:
The x-intercepts are  . These values would be obtained if the original quadratic were factored, or reverse-FOILed and the factors were set equal to zero.
. These values would be obtained if the original quadratic were factored, or reverse-FOILed and the factors were set equal to zero.
For  ,
,  . For
. For  ,
,  . These equations determine the resulting factors and the resulting function;
. These equations determine the resulting factors and the resulting function;  .
.
Multiplying the factors and simplifying,
 .
.
Answer:  .
.
Method 2:
Use the form  , where
, where  is the vertex.
is the vertex.
 is
is  , so
, so  ,
,  .
.
![(x - $[-4])^{2}$ + (-4) = (x + $4)^{2}$ - 4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/478227/gif.latex)
Answer: 



Method 1:
The x-intercepts are 
For 




Multiplying the factors and simplifying,

Answer: 
Method 2:
Use the form 





Answer:
Write the quadratic function for the graph:

Write the quadratic function for the graph:

Tap to see back →
Because there are no x-intercepts, use the form  , where vertex
, where vertex  is
is  , so
, so  ,
,  , which gives
, which gives





Because there are no x-intercepts, use the form 




Which could be the equation for this graph?

Which could be the equation for this graph?
Tap to see back →
This graph has zeros at 3, -2, and -4.5. This means that  ,
,  , and
, and  . That last root is easier to work with if we consider it as
. That last root is easier to work with if we consider it as  and simplify it to
and simplify it to  . Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.
. Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.
Our equation results from multiplying  , which results in
, which results in  .
.
This graph has zeros at 3, -2, and -4.5. This means that 




Our equation results from multiplying 

Write the equation for the polynomial in this graph:

Write the equation for the polynomial in this graph:

Tap to see back →
The zeros for this polynomial are  .
.
This means that the factors are equal to zero when these values are plugged in for x.
 multiply both sides by 2
multiply both sides by 2
 so one factor is
so one factor is 
 multiply both sides by 3
multiply both sides by 3
 so one factor is
so one factor is 
 so one factor is
so one factor is 
Multiply these three factors:



The zeros for this polynomial are 
This means that the factors are equal to zero when these values are plugged in for x.





Multiply these three factors:
Write the equation for the polynomial shown in this graph:

Write the equation for the polynomial shown in this graph:

Tap to see back →
The zeros of this polynomial are  . This means that the factors equal zero when these values are plugged in.
. This means that the factors equal zero when these values are plugged in.
One factor is 
One factor is 
The third factor is equivalent to  . Set equal to 0 and multiply by 2:
. Set equal to 0 and multiply by 2:


Multiply these three factors:


The graph is negative since it goes down then up then down, so we have to switch all of the signs:

The zeros of this polynomial are 
One factor is
One factor is
The third factor is equivalent to 
Multiply these three factors:
The graph is negative since it goes down then up then down, so we have to switch all of the signs:
Write the equation for the polynomial in this graph:

Write the equation for the polynomial in this graph:

Tap to see back →
The zeros for this polynomial are  . That means that the factors are equal to zero when these values are plugged in.
. That means that the factors are equal to zero when these values are plugged in.
 or equivalently
or equivalently  multiply both sides by 4
multiply both sides by 4
 the first factor is
the first factor is 
 multiply both sides by 3
multiply both sides by 3
 the second factor is
the second factor is 
 the third factor is
the third factor is 
Multiply the three factors:



The zeros for this polynomial are 






Multiply the three factors: