Integers - PSAT Math
Card 0 of 1267
A baker has four different types of frosting, three different kinds of sprinkles, and 8 different cookie cutters. How many different cookie combinations can the baker create if each cookie has one type of frosting and one type of sprinkle?
A baker has four different types of frosting, three different kinds of sprinkles, and 8 different cookie cutters. How many different cookie combinations can the baker create if each cookie has one type of frosting and one type of sprinkle?
Tap to see back →
Since this a combination problem and we want to know how many different ways the cookies can be created we can solve this using the Fundamental counting principle. 4 x 3 x 8 = 96
Multiplying each of the possible choices together.
Since this a combination problem and we want to know how many different ways the cookies can be created we can solve this using the Fundamental counting principle. 4 x 3 x 8 = 96
Multiplying each of the possible choices together.
If x and y are integers and at least one of them is even, which of the following MUST be true?
If x and y are integers and at least one of them is even, which of the following MUST be true?
Tap to see back →
Since we are only told that "at least" one of the numbers is even, we could have one even and one odd integer OR we could have two even integers.
Even plus odd is odd, but even plus even is even, so x + y could be either even or odd.
Even times odd is even, and even times even is even, so xy must be even.
Since we are only told that "at least" one of the numbers is even, we could have one even and one odd integer OR we could have two even integers.
Even plus odd is odd, but even plus even is even, so x + y could be either even or odd.
Even times odd is even, and even times even is even, so xy must be even.
If xy = 100 and x and y are distinct positive integers, what is the smallest possible value of x + y?
If xy = 100 and x and y are distinct positive integers, what is the smallest possible value of x + y?
Tap to see back →
Consider the possible values for (x, y):
(1, 100)
(2, 50)
(4, 25)
(5, 20)
Note that (10, 10) is not possible since the two variables are to be distinct. The sums of the above pairs, respectively, are:
1 + 100 = 101
2 + 50 = 52
4 + 25 = 29
5 + 20 = 25, the smallest possible value.
Consider the possible values for (x, y):
(1, 100)
(2, 50)
(4, 25)
(5, 20)
Note that (10, 10) is not possible since the two variables are to be distinct. The sums of the above pairs, respectively, are:
1 + 100 = 101
2 + 50 = 52
4 + 25 = 29
5 + 20 = 25, the smallest possible value.
Which of the following is not a rational number?
Which of the following is not a rational number?
Tap to see back →
A rational number is a number that can be written in the form of a/b, where a and b are integers, aka a real number that can be written as a simple fraction or ratio. 4 of the 5 answer choices can be written as fractions and are thus rational.
5 = 5/1, 1.75 = 7/4, .001 = 1/1000, 0.111... = 1/9
√2 cannot be written as a fraction because it is irrational. The two most famous irrational numbers are √2 and pi.
A rational number is a number that can be written in the form of a/b, where a and b are integers, aka a real number that can be written as a simple fraction or ratio. 4 of the 5 answer choices can be written as fractions and are thus rational.
5 = 5/1, 1.75 = 7/4, .001 = 1/1000, 0.111... = 1/9
√2 cannot be written as a fraction because it is irrational. The two most famous irrational numbers are √2 and pi.
Four consecutive integers have a mean of 9.5. What is the largest of these integers?
Four consecutive integers have a mean of 9.5. What is the largest of these integers?
Tap to see back →
Four consecutive integers could be represented as n, n+1, n+2, n+3
Therefore, by saying that they have a mean of 9.5, we mean to say:
(n + n+1 + n+2 + n+ 3)/4 = 9.5
(4n + 6)/4 = 9.5 → 4n + 6 = 38 → 4n = 32 → n = 8
Therefore, the largest value is n + 3, or 11.
Four consecutive integers could be represented as n, n+1, n+2, n+3
Therefore, by saying that they have a mean of 9.5, we mean to say:
(n + n+1 + n+2 + n+ 3)/4 = 9.5
(4n + 6)/4 = 9.5 → 4n + 6 = 38 → 4n = 32 → n = 8
Therefore, the largest value is n + 3, or 11.
-27, -24, -21, -18…
In the sequence above, each term after the first is 3 greater than the preceding term. Which of the following could not be a value in the sequence?
-27, -24, -21, -18…
In the sequence above, each term after the first is 3 greater than the preceding term. Which of the following could not be a value in the sequence?
Tap to see back →
All of the values in the sequence must be a multiple of 3. All answers are multiples of 3 except 461 so 461 cannot be part of the sequence.
All of the values in the sequence must be a multiple of 3. All answers are multiples of 3 except 461 so 461 cannot be part of the sequence.
What property of arithmetic is demonstrated here?
If  and
and  , then
, then  .
.
What property of arithmetic is demonstrated here?
If 


Tap to see back →
The symbols express the idea that if a number is less than a second number, which is less than a third, then the first number is less than the third. This is the transitive property of inequality.
The symbols express the idea that if a number is less than a second number, which is less than a third, then the first number is less than the third. This is the transitive property of inequality.
Suppose you know the values of the variables in the expression

and you wish to evaluate it.
Which operation do you execute last?
Suppose you know the values of the variables in the expression
and you wish to evaluate it.
Which operation do you execute last?
Tap to see back →
In the absence of grouping symbols, the first operations that should be carried out are exponentiations, followed by multiplications and divisions, followed by additions and subtractions.
The additions and subtractions are carried out from left to right. Since the addition is the one to the right, it is performed last.
In the absence of grouping symbols, the first operations that should be carried out are exponentiations, followed by multiplications and divisions, followed by additions and subtractions.
The additions and subtractions are carried out from left to right. Since the addition is the one to the right, it is performed last.
The annual number of cellular phones purchased from a company is illustrated in the following graph. How many more phones were sold in 2009 than 2011?
![]()
The annual number of cellular phones purchased from a company is illustrated in the following graph. How many more phones were sold in 2009 than 2011?
Tap to see back →
In 2009, 32,000 phones were sold (according the the label on the y-axis, each number is equal to 1,000 phones). In 2011, 26,000 phones were sold.
32,000-26,000=6,000
In 2009, 32,000 phones were sold (according the the label on the y-axis, each number is equal to 1,000 phones). In 2011, 26,000 phones were sold.
32,000-26,000=6,000
If  , what is the value of
, what is the value of  ?
?
If 

Tap to see back →
Substitute – 4 in for x. Remember that when a negative number is raised to the third power, it is negative. - = – 64. – 64 – 36 = – 100. Since you are asked to take the absolute value of – 100 the final value of f(-4) = 100. The absolute value of any number is positive.
Substitute – 4 in for x. Remember that when a negative number is raised to the third power, it is negative. - = – 64. – 64 – 36 = – 100. Since you are asked to take the absolute value of – 100 the final value of f(-4) = 100. The absolute value of any number is positive.
Let  and
and  both be negative numbers such that
both be negative numbers such that  and
and  . What is
. What is  ?
?
Let 




Tap to see back →
We need to solve the two equations |2a – 3| = 5 and |3 – 4b| = 11, in order to determine the possible values of a and b. When solving equations involving absolute values, we must remember to consider both the positive and negative cases. For example, if |x| = 4, then x can be either 4 or –4.
Let's look at |2a – 3| = 5. The two equations we need to solve are 2a – 3 = 5 and 2a – 3 = –5.
2a – 3 = 5 or 2a – 3 = –5
Add 3 to both sides.
2a = 8 or 2a = –2
Divide by 2.
a = 4 or a = –1
Therefore, the two possible values for a are 4 and –1. However, the problem states that both a and b are negative. Thus, a must equal –1.
Let's now find the values of b.
3 – 4b = 11 or 3 – 4b = –11
Subtract 3 from both sides.
–4b = 8 or –4b = –14
Divide by –4.
b = –2 or b = 7/2
Since b must also be negative, b must equal –2.
We have determined that a is –1 and b is –2. The original question asks us to find |b – a|.
|b – a| = |–2 – (–1)| = | –2 + 1 | = |–1| = 1.
The answer is 1.
We need to solve the two equations |2a – 3| = 5 and |3 – 4b| = 11, in order to determine the possible values of a and b. When solving equations involving absolute values, we must remember to consider both the positive and negative cases. For example, if |x| = 4, then x can be either 4 or –4.
Let's look at |2a – 3| = 5. The two equations we need to solve are 2a – 3 = 5 and 2a – 3 = –5.
2a – 3 = 5 or 2a – 3 = –5
Add 3 to both sides.
2a = 8 or 2a = –2
Divide by 2.
a = 4 or a = –1
Therefore, the two possible values for a are 4 and –1. However, the problem states that both a and b are negative. Thus, a must equal –1.
Let's now find the values of b.
3 – 4b = 11 or 3 – 4b = –11
Subtract 3 from both sides.
–4b = 8 or –4b = –14
Divide by –4.
b = –2 or b = 7/2
Since b must also be negative, b must equal –2.
We have determined that a is –1 and b is –2. The original question asks us to find |b – a|.
|b – a| = |–2 – (–1)| = | –2 + 1 | = |–1| = 1.
The answer is 1.
For which of the following functions below does f(x) = |f(x)| for every value of x within its domain?
For which of the following functions below does f(x) = |f(x)| for every value of x within its domain?
Tap to see back →
When we take the absolute value of a function, any negative values get changed into positive values. Essentially, |f(x)| will take all of the negative values of f(x) and reflect them across the x-axis. However, any values of f(x) that are positive or equal to zero will not be changed, because the absolute value of a positive number (or zero) is still the same number.
If we can show that f(x) has negative values, then |f(x)| will be different from f(x) at some points, because its negative values will be changed to positive values. In other words, our answer will consist of the function that never has negative values.
Let's look at f(x) = 2_x_ + 3. Obviously, this equation of a line will have negative values. For example, where x = –4, f(–4) = 2(–4) + 3 = –5, which is negative. Thus, f(x) has negative values, and if we were to graph |f(x)|, the result would be different from f(x). Therefore, f(x) = 2_x_ + 3 isn't the correct answer.
Next, let's look at f(x) = _x_2 – 9. If we let x = 1, then f(1) = 1 – 9 = –8, which is negative. Thus |f(x)| will not be the same as f(x), and we can eliminate this choice as well.
Now, let's examine f(x) = x_2 – 2_x. We know that _x_2 by itself can never be negative. However, if x_2 is really small, then adding –2_x could make it negative. Therefore, let's evaluate f(x) when x is a fractional value such as 1/2. f(1/2) = 1/4 – 1 = –3/4, which is negative. Thus, there are some values on f(x) that are negative, so we can eliminate this function.
Next, let's examine f(x) = _x_4 + x. In general, any number taken to an even-numbered power must always be non-negative. Therefore, _x_4 cannot be negative, because if we multiplied a negative number by itself four times, the result would be positive. However, the x term could be negative. If we let x be a small negative fraction, then _x_4 would be close to zero, and we would be left with x, which is negative. For example, let's find f(x) when x = –1/2. f(–1/2) = (–1/2)4 + (–1/2) = (1/16) – (1/2) = –7/16, which is negative. Thus, |f(x)| is not always the same as f(x).
By process of elimination, the answer is f(x) = _x_4 + (1 – x)2 . This makes sense because _x_4 can't be negative, and because (1 – x)2 can't be negative. No matter what we subtract from one, when we square the final result, we can't get a negative number. And if we add _x_4 and (1 – x)2, the result will also be non-negative, because adding two non-negative numbers always produces a non-negative result. Therefore, f(x) = _x_4 + (1 – x)2 will not have any negative values, and |f(x)| will be the same as f(x) for all values of x.
The answer is f(x) = _x_4 + (1 – x)2 .
When we take the absolute value of a function, any negative values get changed into positive values. Essentially, |f(x)| will take all of the negative values of f(x) and reflect them across the x-axis. However, any values of f(x) that are positive or equal to zero will not be changed, because the absolute value of a positive number (or zero) is still the same number.
If we can show that f(x) has negative values, then |f(x)| will be different from f(x) at some points, because its negative values will be changed to positive values. In other words, our answer will consist of the function that never has negative values.
Let's look at f(x) = 2_x_ + 3. Obviously, this equation of a line will have negative values. For example, where x = –4, f(–4) = 2(–4) + 3 = –5, which is negative. Thus, f(x) has negative values, and if we were to graph |f(x)|, the result would be different from f(x). Therefore, f(x) = 2_x_ + 3 isn't the correct answer.
Next, let's look at f(x) = _x_2 – 9. If we let x = 1, then f(1) = 1 – 9 = –8, which is negative. Thus |f(x)| will not be the same as f(x), and we can eliminate this choice as well.
Now, let's examine f(x) = x_2 – 2_x. We know that _x_2 by itself can never be negative. However, if x_2 is really small, then adding –2_x could make it negative. Therefore, let's evaluate f(x) when x is a fractional value such as 1/2. f(1/2) = 1/4 – 1 = –3/4, which is negative. Thus, there are some values on f(x) that are negative, so we can eliminate this function.
Next, let's examine f(x) = _x_4 + x. In general, any number taken to an even-numbered power must always be non-negative. Therefore, _x_4 cannot be negative, because if we multiplied a negative number by itself four times, the result would be positive. However, the x term could be negative. If we let x be a small negative fraction, then _x_4 would be close to zero, and we would be left with x, which is negative. For example, let's find f(x) when x = –1/2. f(–1/2) = (–1/2)4 + (–1/2) = (1/16) – (1/2) = –7/16, which is negative. Thus, |f(x)| is not always the same as f(x).
By process of elimination, the answer is f(x) = _x_4 + (1 – x)2 . This makes sense because _x_4 can't be negative, and because (1 – x)2 can't be negative. No matter what we subtract from one, when we square the final result, we can't get a negative number. And if we add _x_4 and (1 – x)2, the result will also be non-negative, because adding two non-negative numbers always produces a non-negative result. Therefore, f(x) = _x_4 + (1 – x)2 will not have any negative values, and |f(x)| will be the same as f(x) for all values of x.
The answer is f(x) = _x_4 + (1 – x)2 .
Tap to see back →
Evaluate  if
if  .
.
Evaluate 

Tap to see back →
Remember that the absolute value of a number is the positive value of that number. It is important to know what absolute value represents: the distance of any given number from the number 0. For that reason, absolute value cannot be negative, and we can eliminate  and
and  from our answer choices
from our answer choices
To solve, substitute  into the equation, taking extra care to correctly calculate the negative numbers:
into the equation, taking extra care to correctly calculate the negative numbers:






The answer is 12.
Remember that the absolute value of a number is the positive value of that number. It is important to know what absolute value represents: the distance of any given number from the number 0. For that reason, absolute value cannot be negative, and we can eliminate 

To solve, substitute 
The answer is 12.
Which of the following could represent the sum of 3 consecutive odd integers, given that d is one of the three?
Which of the following could represent the sum of 3 consecutive odd integers, given that d is one of the three?
Tap to see back →
If the largest of the three consecutive odd integers is d, then the three numbers are (in descending order):
d, d – 2, d – 4
This is true because consecutive odd integers always differ by two. Adding the three expressions together, we see that the sum is 3_d_ – 6.
If the largest of the three consecutive odd integers is d, then the three numbers are (in descending order):
d, d – 2, d – 4
This is true because consecutive odd integers always differ by two. Adding the three expressions together, we see that the sum is 3_d_ – 6.
How many of these statements are correct?
I) 
II) 
III) 
IV) 
How many of these statements are correct?
I)
II)
III)
IV)
Tap to see back →
The absolute value of a nonnegative number is the number itself; the absolute value of a negative number can be obtained by removing the negative symbol. Therefore,
 .
.
The four statements can be rewritten as:
Both I and III)  - This is true.
- This is true.
Both II and IV)  - This is false.
- This is false.
The correct response is two.
The absolute value of a nonnegative number is the number itself; the absolute value of a negative number can be obtained by removing the negative symbol. Therefore,

The four statements can be rewritten as:
Both I and III) 
Both II and IV) 
The correct response is two.

If the tick marks are equally spaced on the number line above, what is the average (arithmetic mean) of x, y, and z?
If the tick marks are equally spaced on the number line above, what is the average (arithmetic mean) of x, y, and z?
Tap to see back →
First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.
Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.
Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).
Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.
First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.
Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.
Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).
Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.
How many numbers 1 to 250 inclusive are cubes of integers?
How many numbers 1 to 250 inclusive are cubes of integers?
Tap to see back →
The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.
The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.

Refer to the above number line. Which of the points is most likely the location of the number  ?
?

Refer to the above number line. Which of the points is most likely the location of the number 
Tap to see back →
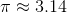 , so
, so 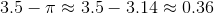
Therefore,

On the number line,  appears between 0.3 and 0.4 and is the correct choice.
appears between 0.3 and 0.4 and is the correct choice.
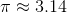
Therefore,
On the number line, 
If 0 < n < 1, then which of the following is the smallest?
If 0 < n < 1, then which of the following is the smallest?
Tap to see back →
First, it will help us to determine which of the answer choices are positive and which are negative.
Because n is positive, we know that n2 is positive, because any number squared is positive. Similarly, 1/n2 is also positive.
Let's look at the answer choice –1/n. This must be negative, because a negative number divided by a positive one will give us a negative number. Similarly, –1/n3 will also be negative.
The last choice is n3 – 1. We are told that 0 < n < 1. Because n is a positive value less than one, we know that 0 < n3 < n2 < n < 1. In other words, n3 will be a small positive value, but it will still be less than one. Thus, because n3 < 1, if we subtract 1 from both sides, we see that n3 – 1 < 0. Therefore, n3 - 1 is a negative value.
All negative numbers are less than positive numbers. Thus, we can eliminate n2 and 1/n2, which are both positive. We are left with –1/n, –1/n3, and n3 – 1.
Let us compare –1/n and –1/n3. First, let us assume that –1/n < –1/n3.
–1/n < –1/n3
Multiply both sides by n3. We don't need to switch the signs because n3 is positive.
–n2 < –1
Multiply both sides by –1.
n2 > 1.
We know that n2 will only be bigger than 1 when n > 1 or if n < –1. But we know that 0 < n < 1, so –1/n is not less than –1/n3. Therefore, –1/n3 must be smaller.
Finally, let's compare –1/n3 and n3 – 1. Let us assume that –1/n3 < n3 – 1.
–1/n3 < n3 – 1
Multiply both sides by n3.
–1 < n6 – n3
Add one to both sides.
n6 – n3 + 1 > 0. If this inequality is true, then it will be true that –1/n3 is the smallest number.
Here it will be helpful to try some values for n. Let's pick n = 1/2 and see what happens. It will help to use our calculator.
(1/2)6 – (1/2)3 + 1 = 0.891 > 0.
Therefore, we suspect that because n6 – n3 + 1 > 0, –1/n3 is indeed the smallest number. We can verify this by trying more values of n.
The answer is –1/n3.
First, it will help us to determine which of the answer choices are positive and which are negative.
Because n is positive, we know that n2 is positive, because any number squared is positive. Similarly, 1/n2 is also positive.
Let's look at the answer choice –1/n. This must be negative, because a negative number divided by a positive one will give us a negative number. Similarly, –1/n3 will also be negative.
The last choice is n3 – 1. We are told that 0 < n < 1. Because n is a positive value less than one, we know that 0 < n3 < n2 < n < 1. In other words, n3 will be a small positive value, but it will still be less than one. Thus, because n3 < 1, if we subtract 1 from both sides, we see that n3 – 1 < 0. Therefore, n3 - 1 is a negative value.
All negative numbers are less than positive numbers. Thus, we can eliminate n2 and 1/n2, which are both positive. We are left with –1/n, –1/n3, and n3 – 1.
Let us compare –1/n and –1/n3. First, let us assume that –1/n < –1/n3.
–1/n < –1/n3
Multiply both sides by n3. We don't need to switch the signs because n3 is positive.
–n2 < –1
Multiply both sides by –1.
n2 > 1.
We know that n2 will only be bigger than 1 when n > 1 or if n < –1. But we know that 0 < n < 1, so –1/n is not less than –1/n3. Therefore, –1/n3 must be smaller.
Finally, let's compare –1/n3 and n3 – 1. Let us assume that –1/n3 < n3 – 1.
–1/n3 < n3 – 1
Multiply both sides by n3.
–1 < n6 – n3
Add one to both sides.
n6 – n3 + 1 > 0. If this inequality is true, then it will be true that –1/n3 is the smallest number.
Here it will be helpful to try some values for n. Let's pick n = 1/2 and see what happens. It will help to use our calculator.
(1/2)6 – (1/2)3 + 1 = 0.891 > 0.
Therefore, we suspect that because n6 – n3 + 1 > 0, –1/n3 is indeed the smallest number. We can verify this by trying more values of n.
The answer is –1/n3.




