Whole and Part - PSAT Math
Card 0 of 112
Mr. Owens spent $7.50 for a dinner buffet. The amount he paid accounted for 3/4 of the money in his wallet. How much money is left in his wallet for other expenses?
Mr. Owens spent $7.50 for a dinner buffet. The amount he paid accounted for 3/4 of the money in his wallet. How much money is left in his wallet for other expenses?
Tap to see back →
If $7.50 is 3/4 of the total, 7.50/3 gives us what 1/4 of his total money would be. This equals $2.50, the remaining unspent quarter.
If $7.50 is 3/4 of the total, 7.50/3 gives us what 1/4 of his total money would be. This equals $2.50, the remaining unspent quarter.
A certain ball that is dropped will bounce back to 3/5 of the height it was initially dropped from. If after the 2nd bounce the ball reaches 39.96 ft, what was the initial height the ball was dropped from?
A certain ball that is dropped will bounce back to 3/5 of the height it was initially dropped from. If after the 2nd bounce the ball reaches 39.96 ft, what was the initial height the ball was dropped from?
Tap to see back →
We know the height of the initial bounce, so work backwards to find the initial height. 39.96/0.6 = 66.6 = height of ball after first bounce
66.6/0.6 = 111 ft
We know the height of the initial bounce, so work backwards to find the initial height. 39.96/0.6 = 66.6 = height of ball after first bounce
66.6/0.6 = 111 ft
If a TV show is 45 minutes long, what fraction of the show is completed 5 minutes after it begins?
If a TV show is 45 minutes long, what fraction of the show is completed 5 minutes after it begins?
Tap to see back →
5 minutes out of 45 have been completed. We can represent this as a fraction: 5/45. When simplified, this yields 1/9.
5 minutes out of 45 have been completed. We can represent this as a fraction: 5/45. When simplified, this yields 1/9.
A birthday cake is cut into 8 pieces. On the first night three pieces are eaten. On the second night, 20% of the remaining cake was eaten. On the third night, half of the remaining cake was eaten. How many slices were left to eat on the fourth night?
A birthday cake is cut into 8 pieces. On the first night three pieces are eaten. On the second night, 20% of the remaining cake was eaten. On the third night, half of the remaining cake was eaten. How many slices were left to eat on the fourth night?
Tap to see back →
First night: 8 – 3 = 5 remaining.
Second night: 20% of 5 remaining = .2 * 5 = 1 slice Therefore 4 remaining.
Third night: ½ of the 4 remaining = ½*4 = 2 slices remaining
First night: 8 – 3 = 5 remaining.
Second night: 20% of 5 remaining = .2 * 5 = 1 slice Therefore 4 remaining.
Third night: ½ of the 4 remaining = ½*4 = 2 slices remaining
There was a malfunction at a candy factory and the machines only put red, purple, and green candy into the bags. If 1/4 of the candies were red and 3/8 were green, how many purple candies were in the bag, if each bag can hold 16 pieces?
There was a malfunction at a candy factory and the machines only put red, purple, and green candy into the bags. If 1/4 of the candies were red and 3/8 were green, how many purple candies were in the bag, if each bag can hold 16 pieces?
Tap to see back →
Since 1/4 of the 16 are red: 16 * 1/4 = 4 red candies. With 3/8 being green:
16 X 3/8 = 6 green candies. 16 – 4 – 6 = 6 candies remain, which must be purple.
Since 1/4 of the 16 are red: 16 * 1/4 = 4 red candies. With 3/8 being green:
16 X 3/8 = 6 green candies. 16 – 4 – 6 = 6 candies remain, which must be purple.
In the 30-day month of January, for every three days it snowed, there were seven days it did not snow. The number of days in January on which it did not snow was how much greater than the number of days in January on which it snowed?
In the 30-day month of January, for every three days it snowed, there were seven days it did not snow. The number of days in January on which it did not snow was how much greater than the number of days in January on which it snowed?
Tap to see back →
The question tells us that for every ten-day period in January (a three-day period plus a seven-day period), it snowed on 3 of those days and did not snow on 7 of those days. Since January has 30 days, it has 3 ten-day periods, so we multiply the numbers given for the 10-day period by 3 to find the number of days with and without snow during the 30-day period. Doing this, we see that it snowed 3 * 3 = 9 days and did not snow 7 * 3 = 21 days during the 30-day period. Since the question asks how much greater the number of days on which it did not snow is than the number of days on which it snowed, we subtract as follows: number of days it did not snow - number of days it snowed = 21 – 9 = 12.
The question tells us that for every ten-day period in January (a three-day period plus a seven-day period), it snowed on 3 of those days and did not snow on 7 of those days. Since January has 30 days, it has 3 ten-day periods, so we multiply the numbers given for the 10-day period by 3 to find the number of days with and without snow during the 30-day period. Doing this, we see that it snowed 3 * 3 = 9 days and did not snow 7 * 3 = 21 days during the 30-day period. Since the question asks how much greater the number of days on which it did not snow is than the number of days on which it snowed, we subtract as follows: number of days it did not snow - number of days it snowed = 21 – 9 = 12.
Mikey has one full box of cereal. On Saturday, he eats 1/3 of the the box. On Sunday he eats 2/3 of what is left. How much of the box is still left?
Mikey has one full box of cereal. On Saturday, he eats 1/3 of the the box. On Sunday he eats 2/3 of what is left. How much of the box is still left?
Tap to see back →
If Mikey eats 1/3 of the box, he is left with 1 – 1/3 = 2/3.
When he eats 2/3 of what remains, he is eating 2/3 of 2/3, or 4/9 of the box.
2/3 – 4/9 = 2/9
If Mikey eats 1/3 of the box, he is left with 1 – 1/3 = 2/3.
When he eats 2/3 of what remains, he is eating 2/3 of 2/3, or 4/9 of the box.
2/3 – 4/9 = 2/9
What is the remainder when 27 is divided by 6?
What is the remainder when 27 is divided by 6?
Tap to see back →
Long division is the fastest way: 6 goes into 27 four times. 6 times four is 24. 27 – 24 = 3.
Long division is the fastest way: 6 goes into 27 four times. 6 times four is 24. 27 – 24 = 3.
A pitcher is currently $\frac{4}{5}$ of the way full of water. If 3 ounces are poured out, then the pitcher would be 
of the way full. How many ounces of water are in the pitcher before the 3 ounces are poured out?
A pitcher is currently $\frac{4}{5}$ of the way full of water. If 3 ounces are poured out, then the pitcher would be
Tap to see back →
Let p represent the total capacity of the pitcher. The current volume in the pitcher is $\frac{4}{5}$p. If this volume is depleted by 3 ounces, it becomes $\frac{3}{4}$p. In other words:
$\frac{4}{5}$p - 3 = $\frac{3}{4}$p
Solve this equation for p and get:
$\frac{4}{5}$p-$\frac{3}{4}$p=3
$\frac{16}{20}$p-$\frac{15}{20}$p=3
$\frac{1}{20}$p=3
p=60
Remember, p represents the total capacity of the pitcher, or 60 ounces. The question asks how many ounces are in the pitcher at the beginning of the problem, so evaluate$\frac{4}{5}$p=\frac{4}{5}$times 60=48.
Let p represent the total capacity of the pitcher. The current volume in the pitcher is $\frac{4}{5}$p. If this volume is depleted by 3 ounces, it becomes $\frac{3}{4}$p. In other words:
$\frac{4}{5}$p - 3 = $\frac{3}{4}$p
Solve this equation for p and get:
$\frac{4}{5}$p-$\frac{3}{4}$p=3
$\frac{16}{20}$p-$\frac{15}{20}$p=3
$\frac{1}{20}$p=3
p=60
Remember, p represents the total capacity of the pitcher, or 60 ounces. The question asks how many ounces are in the pitcher at the beginning of the problem, so evaluate$\frac{4}{5}$p=\frac{4}{5}$times 60=48.
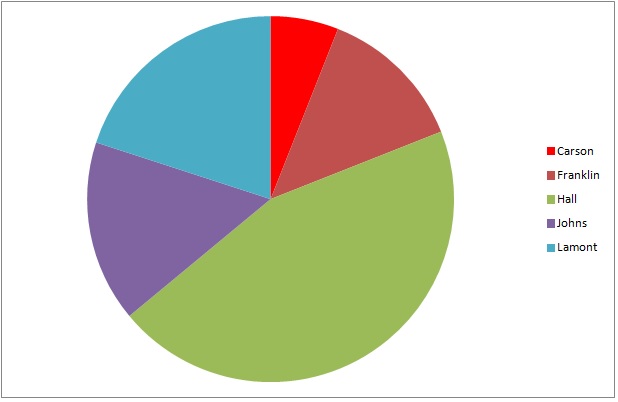
The above graph represents the results of a general election for mayor of Kingston.
If 6,239 people voted in the election, which is closest to the number of people who voted for Johns?
The above graph represents the results of a general election for mayor of Kingston.
If 6,239 people voted in the election, which is closest to the number of people who voted for Johns?
Tap to see back →
The dark purple wedge, which represents Johns, is about one-sixth of the circle, so roughly one-sixth of the voters chose him. This is about
so 1,000 is the best choice among the ones given.
The dark purple wedge, which represents Johns, is about one-sixth of the circle, so roughly one-sixth of the voters chose him. This is about
so 1,000 is the best choice among the ones given.
Kim weighs two-thirds as much as Jim. Jim weighs 50 pounds more than Tim. Together, Kim, Jim and Tim weight 430 pounds. How much do Jim and Kim weigh together?
Kim weighs two-thirds as much as Jim. Jim weighs 50 pounds more than Tim. Together, Kim, Jim and Tim weight 430 pounds. How much do Jim and Kim weigh together?
Tap to see back →
Create an equation to represent the combined weights, in pounds, of Kim, Jim and Tim.
Now, taking the other information we are given, put the weights of Kim and Tim in terms of Jim:
Kim weighs two-thirds of Jim:
Jim weighs 50 pounds more than Tim is the same as saying that Tim weighs 50 pounds less than Jim:
Replace the variables of Kim and Jim in the equation with their substitutions:
Solve for Jim's weight. To combine the fractions, put all variables in terms of thirds and combine like variables:
Jim weighs 180 pounds. Kim weighs two-thirds of 180:
The combined weight of Jim and Kim is equal to:
Create an equation to represent the combined weights, in pounds, of Kim, Jim and Tim.
Now, taking the other information we are given, put the weights of Kim and Tim in terms of Jim:
Kim weighs two-thirds of Jim:
Jim weighs 50 pounds more than Tim is the same as saying that Tim weighs 50 pounds less than Jim:
Replace the variables of Kim and Jim in the equation with their substitutions:
Solve for Jim's weight. To combine the fractions, put all variables in terms of thirds and combine like variables:
Jim weighs 180 pounds. Kim weighs two-thirds of 180:
The combined weight of Jim and Kim is equal to:
There are 60 ties on a rack in the department store. One-third are blue, two-fifths are green, and the remainder are red. How many red ties are on the rack in the department store?
There are 60 ties on a rack in the department store. One-third are blue, two-fifths are green, and the remainder are red. How many red ties are on the rack in the department store?
Tap to see back →
Begin by finding how many blue and green ties there are in the department store. If one-third of 60 ties are blue, then there are 20 blue ties:
Addtionally, if two-fifths of the ties are green, then there are 24 green ties:
To find the number of red ties, subtract the green and blue ties from the total number:
There are 16 red ties in the department store.
Begin by finding how many blue and green ties there are in the department store. If one-third of 60 ties are blue, then there are 20 blue ties:
Addtionally, if two-fifths of the ties are green, then there are 24 green ties:
To find the number of red ties, subtract the green and blue ties from the total number:
There are 16 red ties in the department store.
If Mr. Jones’ math class has 8 boys and two-thirds of the class are girls, how many total students are in the class?
If Mr. Jones’ math class has 8 boys and two-thirds of the class are girls, how many total students are in the class?
Tap to see back →
If two-thirds of the class are girls, then one-third must be boys. Set up an equation comparing the number of boys to how much they represent in the entire class:
8 = (1/3) x, where x is the number in the entire class.
When we solve for x in the equation we get x = 24.
If two-thirds of the class are girls, then one-third must be boys. Set up an equation comparing the number of boys to how much they represent in the entire class:
8 = (1/3) x, where x is the number in the entire class.
When we solve for x in the equation we get x = 24.
A pitcher of water is filled $\frac{2}{5}$ of full. An additional 27 ounces of water is added. Now the pitcher of water is completely full. How much water does the pitcher hold?
A pitcher of water is filled $\frac{2}{5}$ of full. An additional 27 ounces of water is added. Now the pitcher of water is completely full. How much water does the pitcher hold?
Tap to see back →
If 27 ounces fills the pitcher, then it must equal the volume of $\frac{3}{5}$ of the pitcher. If $\frac{3}{5}$ of a pitcher equals 27 ounces, then $\frac{1}{5}$ of a pitcher equals 27div 3=9ounces. Since there are 5 fifths in the pitcher, it must hold 9times 5=45 ounces total.
If 27 ounces fills the pitcher, then it must equal the volume of $\frac{3}{5}$ of the pitcher. If $\frac{3}{5}$ of a pitcher equals 27 ounces, then $\frac{1}{5}$ of a pitcher equals 27div 3=9ounces. Since there are 5 fifths in the pitcher, it must hold 9times 5=45 ounces total.
A certain bakery makes chocolate, vanilla, red velvet, and carrot cupcakes in a ratio of 2:3:5:1. If that bakery makes 63 vanilla cupcakes in one day, what is the total number of cupcakes that the bakery made that day?
A certain bakery makes chocolate, vanilla, red velvet, and carrot cupcakes in a ratio of 2:3:5:1. If that bakery makes 63 vanilla cupcakes in one day, what is the total number of cupcakes that the bakery made that day?
Tap to see back →
Because the bakery makes 63 vanilla cupcakes in one day, start by dividing the 63 by the vanilla part of the ratio, which is 3. 
. That means that the bakery made 21 times the basic set of 2 chocolate, 3 vanilla, 5 red velvet, and 1 carrot cupcakes.
Now add up the parts of your ratio: 
. If the bakery only made 3 vanilla cupcakes, then it would have made 11 cupcakes that day. But, because the bakery made 21 times that number of vanilla cupcakes, it made 21 times the total number of cupcakes over the course of the day. To find the total number of cupcakes the bakery made that day, you multiply 
to get 
.
Because the bakery makes 63 vanilla cupcakes in one day, start by dividing the 63 by the vanilla part of the ratio, which is 3.
Now add up the parts of your ratio:
A circle is divided into various sized slices. One slice has an interior angle of 
and an area of 
. What is the circumference of the circle?
A circle is divided into various sized slices. One slice has an interior angle of
Tap to see back →
In order to find the circumference of the cirlce, we will need to find the radius of the circle. We know that a slice with a 40-degree angle has an area of 
. There are 360 degrees in a circle. Therefore, the slice of the circle with an angle of 40 dgrees is one-ninth of the entire circle.
Multiply 
by 9 to find the area of the circle
The area of the circle is 
. Now use the formula for area to find the radius
The radius of the circle is 9. Use the formula for circumference to find the circumference of the circle:
The circumference of the circle is 
.
In order to find the circumference of the cirlce, we will need to find the radius of the circle. We know that a slice with a 40-degree angle has an area of
Multiply
The area of the circle is
The radius of the circle is 9. Use the formula for circumference to find the circumference of the circle:
The circumference of the circle is
If a TV show is 45 minutes long, what fraction of the show is completed 5 minutes after it begins?
If a TV show is 45 minutes long, what fraction of the show is completed 5 minutes after it begins?
Tap to see back →
5 minutes out of 45 have been completed. We can represent this as a fraction: 5/45. When simplified, this yields 1/9.
5 minutes out of 45 have been completed. We can represent this as a fraction: 5/45. When simplified, this yields 1/9.
A birthday cake is cut into 8 pieces. On the first night three pieces are eaten. On the second night, 20% of the remaining cake was eaten. On the third night, half of the remaining cake was eaten. How many slices were left to eat on the fourth night?
A birthday cake is cut into 8 pieces. On the first night three pieces are eaten. On the second night, 20% of the remaining cake was eaten. On the third night, half of the remaining cake was eaten. How many slices were left to eat on the fourth night?
Tap to see back →
First night: 8 – 3 = 5 remaining.
Second night: 20% of 5 remaining = .2 * 5 = 1 slice Therefore 4 remaining.
Third night: ½ of the 4 remaining = ½*4 = 2 slices remaining
First night: 8 – 3 = 5 remaining.
Second night: 20% of 5 remaining = .2 * 5 = 1 slice Therefore 4 remaining.
Third night: ½ of the 4 remaining = ½*4 = 2 slices remaining
There was a malfunction at a candy factory and the machines only put red, purple, and green candy into the bags. If 1/4 of the candies were red and 3/8 were green, how many purple candies were in the bag, if each bag can hold 16 pieces?
There was a malfunction at a candy factory and the machines only put red, purple, and green candy into the bags. If 1/4 of the candies were red and 3/8 were green, how many purple candies were in the bag, if each bag can hold 16 pieces?
Tap to see back →
Since 1/4 of the 16 are red: 16 * 1/4 = 4 red candies. With 3/8 being green:
16 X 3/8 = 6 green candies. 16 – 4 – 6 = 6 candies remain, which must be purple.
Since 1/4 of the 16 are red: 16 * 1/4 = 4 red candies. With 3/8 being green:
16 X 3/8 = 6 green candies. 16 – 4 – 6 = 6 candies remain, which must be purple.
In the 30-day month of January, for every three days it snowed, there were seven days it did not snow. The number of days in January on which it did not snow was how much greater than the number of days in January on which it snowed?
In the 30-day month of January, for every three days it snowed, there were seven days it did not snow. The number of days in January on which it did not snow was how much greater than the number of days in January on which it snowed?
Tap to see back →
The question tells us that for every ten-day period in January (a three-day period plus a seven-day period), it snowed on 3 of those days and did not snow on 7 of those days. Since January has 30 days, it has 3 ten-day periods, so we multiply the numbers given for the 10-day period by 3 to find the number of days with and without snow during the 30-day period. Doing this, we see that it snowed 3 * 3 = 9 days and did not snow 7 * 3 = 21 days during the 30-day period. Since the question asks how much greater the number of days on which it did not snow is than the number of days on which it snowed, we subtract as follows: number of days it did not snow - number of days it snowed = 21 – 9 = 12.
The question tells us that for every ten-day period in January (a three-day period plus a seven-day period), it snowed on 3 of those days and did not snow on 7 of those days. Since January has 30 days, it has 3 ten-day periods, so we multiply the numbers given for the 10-day period by 3 to find the number of days with and without snow during the 30-day period. Doing this, we see that it snowed 3 * 3 = 9 days and did not snow 7 * 3 = 21 days during the 30-day period. Since the question asks how much greater the number of days on which it did not snow is than the number of days on which it snowed, we subtract as follows: number of days it did not snow - number of days it snowed = 21 – 9 = 12.