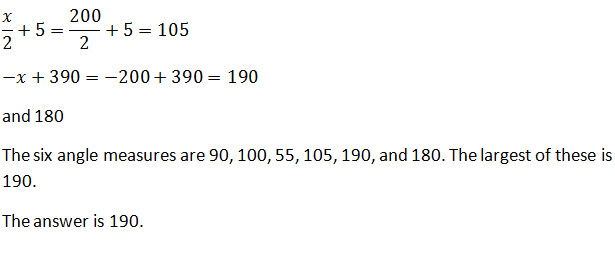How to find an angle in a hexagon - PSAT Math
Card 0 of 49
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
Tap to see back →
The sum of the interior angles of a polygon is given by  where
where  = number of sides of the polygon. An octagon has 8 sides, so the formula becomes
= number of sides of the polygon. An octagon has 8 sides, so the formula becomes 
The sum of the interior angles of a polygon is given by 

In a rectangular hexagon, what is the meaure of each interior angle?
In a rectangular hexagon, what is the meaure of each interior angle?
Tap to see back →
The sum of the interior angles of a hexagon must equal 720 degrees. Because the hexagon is regular, all of the interior angles will have the same measure. A hexagon has six sides and six interior angles. Therefore, each angle measures .
.
The sum of the interior angles of a hexagon must equal 720 degrees. Because the hexagon is regular, all of the interior angles will have the same measure. A hexagon has six sides and six interior angles. Therefore, each angle measures

Note:Figure NOT drawn to scale.
Refer to the above figure. Evaluate  .
.

Note:Figure NOT drawn to scale.
Refer to the above figure. Evaluate 
Tap to see back →
The sum of the degree measures of the angles of a (six-sided) hexagon, is

We can solve for  in the equation
in the equation



The sum of the degree measures of the angles of a (six-sided) hexagon, is
We can solve for 

Note: Figure NOT drawn to scale.
Refer to the above figure. Evaluate  .
.

Note: Figure NOT drawn to scale.
Refer to the above figure. Evaluate 
Tap to see back →
The sum of the degree measures of the angles of a (six-sided) hexagon, is

We can solve for  in the equation
in the equation




The sum of the degree measures of the angles of a (six-sided) hexagon, is
We can solve for 
Three angles of a hexagon measure  . The other three angles are congruent to one another. What is the measure of each of the latter three angles?
. The other three angles are congruent to one another. What is the measure of each of the latter three angles?
Three angles of a hexagon measure 
Tap to see back →
The sum of the degree measures of the angles of a (six-sided) hexagon, is

Let  be the common measure of the three congruent angles in question. We can solve for
be the common measure of the three congruent angles in question. We can solve for  in the equation
in the equation




The sum of the degree measures of the angles of a (six-sided) hexagon, is
Let 

What is the measurement of one of the interior angles of a regular hexagon?
What is the measurement of one of the interior angles of a regular hexagon?
Tap to see back →
To find the sum of the interior angles of any regular polygon, use the formula  , where
, where  represents the number of sides of the regular polygon.
represents the number of sides of the regular polygon.



The sum of the interior angles of a regular hexagon is 720 degrees. To find the measurement of one angle, divide by the number of interior angles (or sides):


The measurement of one angle in a regular hexagon is 120 degrees.
To find the sum of the interior angles of any regular polygon, use the formula 

The sum of the interior angles of a regular hexagon is 720 degrees. To find the measurement of one angle, divide by the number of interior angles (or sides):
The measurement of one angle in a regular hexagon is 120 degrees.
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
Tap to see back →
The sum of the interior angles of a polygon is given by  where
where  = number of sides of the polygon. An octagon has 8 sides, so the formula becomes
= number of sides of the polygon. An octagon has 8 sides, so the formula becomes 
The sum of the interior angles of a polygon is given by 

In a rectangular hexagon, what is the meaure of each interior angle?
In a rectangular hexagon, what is the meaure of each interior angle?
Tap to see back →
The sum of the interior angles of a hexagon must equal 720 degrees. Because the hexagon is regular, all of the interior angles will have the same measure. A hexagon has six sides and six interior angles. Therefore, each angle measures .
.
The sum of the interior angles of a hexagon must equal 720 degrees. Because the hexagon is regular, all of the interior angles will have the same measure. A hexagon has six sides and six interior angles. Therefore, each angle measures

Note:Figure NOT drawn to scale.
Refer to the above figure. Evaluate  .
.

Note:Figure NOT drawn to scale.
Refer to the above figure. Evaluate 
Tap to see back →
The sum of the degree measures of the angles of a (six-sided) hexagon, is

We can solve for  in the equation
in the equation



The sum of the degree measures of the angles of a (six-sided) hexagon, is
We can solve for 

Note: Figure NOT drawn to scale.
Refer to the above figure. Evaluate  .
.

Note: Figure NOT drawn to scale.
Refer to the above figure. Evaluate 
Tap to see back →
The sum of the degree measures of the angles of a (six-sided) hexagon, is

We can solve for  in the equation
in the equation




The sum of the degree measures of the angles of a (six-sided) hexagon, is
We can solve for 
Three angles of a hexagon measure  . The other three angles are congruent to one another. What is the measure of each of the latter three angles?
. The other three angles are congruent to one another. What is the measure of each of the latter three angles?
Three angles of a hexagon measure 
Tap to see back →
The sum of the degree measures of the angles of a (six-sided) hexagon, is

Let  be the common measure of the three congruent angles in question. We can solve for
be the common measure of the three congruent angles in question. We can solve for  in the equation
in the equation




The sum of the degree measures of the angles of a (six-sided) hexagon, is
Let 

What is the measurement of one of the interior angles of a regular hexagon?
What is the measurement of one of the interior angles of a regular hexagon?
Tap to see back →
To find the sum of the interior angles of any regular polygon, use the formula  , where
, where  represents the number of sides of the regular polygon.
represents the number of sides of the regular polygon.



The sum of the interior angles of a regular hexagon is 720 degrees. To find the measurement of one angle, divide by the number of interior angles (or sides):


The measurement of one angle in a regular hexagon is 120 degrees.
To find the sum of the interior angles of any regular polygon, use the formula 

The sum of the interior angles of a regular hexagon is 720 degrees. To find the measurement of one angle, divide by the number of interior angles (or sides):
The measurement of one angle in a regular hexagon is 120 degrees.
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
Tap to see back →
The sum of the interior angles of a polygon is given by  where
where  = number of sides of the polygon. An octagon has 8 sides, so the formula becomes
= number of sides of the polygon. An octagon has 8 sides, so the formula becomes 
The sum of the interior angles of a polygon is given by 

In a rectangular hexagon, what is the meaure of each interior angle?
In a rectangular hexagon, what is the meaure of each interior angle?
Tap to see back →
The sum of the interior angles of a hexagon must equal 720 degrees. Because the hexagon is regular, all of the interior angles will have the same measure. A hexagon has six sides and six interior angles. Therefore, each angle measures .
.
The sum of the interior angles of a hexagon must equal 720 degrees. Because the hexagon is regular, all of the interior angles will have the same measure. A hexagon has six sides and six interior angles. Therefore, each angle measures

Note:Figure NOT drawn to scale.
Refer to the above figure. Evaluate  .
.

Note:Figure NOT drawn to scale.
Refer to the above figure. Evaluate 
Tap to see back →
The sum of the degree measures of the angles of a (six-sided) hexagon, is

We can solve for  in the equation
in the equation



The sum of the degree measures of the angles of a (six-sided) hexagon, is
We can solve for 

Note: Figure NOT drawn to scale.
Refer to the above figure. Evaluate  .
.

Note: Figure NOT drawn to scale.
Refer to the above figure. Evaluate 
Tap to see back →
The sum of the degree measures of the angles of a (six-sided) hexagon, is

We can solve for  in the equation
in the equation




The sum of the degree measures of the angles of a (six-sided) hexagon, is
We can solve for 
Three angles of a hexagon measure  . The other three angles are congruent to one another. What is the measure of each of the latter three angles?
. The other three angles are congruent to one another. What is the measure of each of the latter three angles?
Three angles of a hexagon measure 
Tap to see back →
The sum of the degree measures of the angles of a (six-sided) hexagon, is

Let  be the common measure of the three congruent angles in question. We can solve for
be the common measure of the three congruent angles in question. We can solve for  in the equation
in the equation




The sum of the degree measures of the angles of a (six-sided) hexagon, is
Let