How to find the length of the side of a right triangle - PSAT Math
Card 0 of 77
Bob the Helicopter is at 30,000 ft. above sea level, and as viewed on a map his airport is 40,000 ft. away. If Bob travels in a straight line to his airport at 250 feet per second, how many minutes will it take him to arrive?
Bob the Helicopter is at 30,000 ft. above sea level, and as viewed on a map his airport is 40,000 ft. away. If Bob travels in a straight line to his airport at 250 feet per second, how many minutes will it take him to arrive?
Tap to see back →
Draw a right triangle with a height of 30,000 ft. and a base of 40,000 ft. The hypotenuse, or distance travelled, is then 50,000ft using the Pythagorean Theorem. Then dividing distance by speed will give us time, which is 200 seconds, or 3 minutes and 20 seconds.
Draw a right triangle with a height of 30,000 ft. and a base of 40,000 ft. The hypotenuse, or distance travelled, is then 50,000ft using the Pythagorean Theorem. Then dividing distance by speed will give us time, which is 200 seconds, or 3 minutes and 20 seconds.
A right triangle has two sides, 9 and x, and a hypotenuse of 15. What is x?
A right triangle has two sides, 9 and x, and a hypotenuse of 15. What is x?
Tap to see back →
We can use the Pythagorean Theorem to solve for x.
92 + _x_2 = 152
81 + _x_2 = 225
_x_2 = 144
x = 12
We can use the Pythagorean Theorem to solve for x.
92 + _x_2 = 152
81 + _x_2 = 225
_x_2 = 144
x = 12
Which set of sides could make a right triangle?
Which set of sides could make a right triangle?
Tap to see back →
By virtue of the Pythagorean Theorem, in a right triangle the sum of the squares of the smaller two sides equals the square of the largest side. Only 9, 12, and 15 fit this rule.
By virtue of the Pythagorean Theorem, in a right triangle the sum of the squares of the smaller two sides equals the square of the largest side. Only 9, 12, and 15 fit this rule.
A right triangle with a base of 12 and hypotenuse of 15 is shown below. Find x.

A right triangle with a base of 12 and hypotenuse of 15 is shown below. Find x.

Tap to see back →
Using the Pythagorean Theorem, the height of the right triangle is found to be = √(〖15〗2 –〖12〗2) = 9, so x=9 – 5=4
Using the Pythagorean Theorem, the height of the right triangle is found to be = √(〖15〗2 –〖12〗2) = 9, so x=9 – 5=4
A right triangle has sides of 36 and 39(hypotenuse). Find the length of the third side
A right triangle has sides of 36 and 39(hypotenuse). Find the length of the third side
Tap to see back →
use the pythagorean theorem:
a2 + b2 = c2 ; a and b are sides, c is the hypotenuse
a2 + 1296 = 1521
a2 = 225
a = 15
use the pythagorean theorem:
a2 + b2 = c2 ; a and b are sides, c is the hypotenuse
a2 + 1296 = 1521
a2 = 225
a = 15
A right triangle has one side equal to 5 and its hypotenuse equal to 14. Its third side is equal to:
A right triangle has one side equal to 5 and its hypotenuse equal to 14. Its third side is equal to:
Tap to see back →
The Pythagorean Theorem gives us _a_2 + _b_2 = _c_2 for a right triangle, where c is the hypotenuse and a and b are the smaller sides. Here a is equal to 5 and c is equal to 14, so _b_2 = 142 – 52 = 171. Therefore b is equal to the square root of 171 or approximately 13.07.
The Pythagorean Theorem gives us _a_2 + _b_2 = _c_2 for a right triangle, where c is the hypotenuse and a and b are the smaller sides. Here a is equal to 5 and c is equal to 14, so _b_2 = 142 – 52 = 171. Therefore b is equal to the square root of 171 or approximately 13.07.
Which of the following could NOT be the lengths of the sides of a right triangle?
Which of the following could NOT be the lengths of the sides of a right triangle?
Tap to see back →
We use the Pythagorean Theorem and we calculate that 25 + 49 is not equal to 100.
All of the other answer choices observe the theorem _a_2 + _b_2 = _c_2
We use the Pythagorean Theorem and we calculate that 25 + 49 is not equal to 100.
All of the other answer choices observe the theorem _a_2 + _b_2 = _c_2
The area of a right traingle is 42. One of the legs has a length of 12. What is the length of the other leg?
The area of a right traingle is 42. One of the legs has a length of 12. What is the length of the other leg?
Tap to see back →
Area= $\frac{1}{2}$times basetimes height
42=\frac{1}{2}$times basetimes 12
42=6times base
base=7
Area= $\frac{1}{2}$times basetimes height
42=\frac{1}{2}$times basetimes 12
42=6times base
base=7


If  and
and  , what is the length of
, what is the length of  ?
?

If 


Tap to see back →
AB is the leg adjacent to Angle A and BC is the leg opposite Angle A.
Since we have a  triangle, the opposites sides of those angles will be in the ratio
triangle, the opposites sides of those angles will be in the ratio  .
.
Here, we know the side opposite the sixty degree angle. Thus, we can set that value equal to  .
.




which also means

AB is the leg adjacent to Angle A and BC is the leg opposite Angle A.
Since we have a 

Here, we know the side opposite the sixty degree angle. Thus, we can set that value equal to 
which also means
![]()
Solve for x.
Solve for x.
Tap to see back →
Use the Pythagorean Theorem. Let a = 8 and c = 10 (because it is the hypotenuse)
$a^2$$+x^2$$=c^2$
$8^2$$+x^2$$=10^2$
$64+x^2$=100
$x^2$=100-64=36
x=6
Use the Pythagorean Theorem. Let a = 8 and c = 10 (because it is the hypotenuse)
$a^2$$+x^2$$=c^2$
$8^2$$+x^2$$=10^2$
$64+x^2$=100
$x^2$=100-64=36
x=6

Note: Figure NOT drawn to scale.
Refer to the above diagram. Evaluate 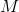 .
.

Note: Figure NOT drawn to scale.
Refer to the above diagram. Evaluate 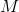
Tap to see back →
The altitude perpendicular to the hypotenuse of a right triangle divides that triangle into two smaller triangles similar to each other and the large triangle. Therefore, the sides are in proportion. The hypotenuse of the triangle is equal to

Therefore, we can set up, and solve for 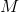 in, a proportion statement involving the shorter side and hypotenuse of the large triangle and the larger of the two smaller triangles:
in, a proportion statement involving the shorter side and hypotenuse of the large triangle and the larger of the two smaller triangles:



The altitude perpendicular to the hypotenuse of a right triangle divides that triangle into two smaller triangles similar to each other and the large triangle. Therefore, the sides are in proportion. The hypotenuse of the triangle is equal to
Therefore, we can set up, and solve for 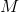
Bob the Helicopter is at 30,000 ft. above sea level, and as viewed on a map his airport is 40,000 ft. away. If Bob travels in a straight line to his airport at 250 feet per second, how many minutes will it take him to arrive?
Bob the Helicopter is at 30,000 ft. above sea level, and as viewed on a map his airport is 40,000 ft. away. If Bob travels in a straight line to his airport at 250 feet per second, how many minutes will it take him to arrive?
Tap to see back →
Draw a right triangle with a height of 30,000 ft. and a base of 40,000 ft. The hypotenuse, or distance travelled, is then 50,000ft using the Pythagorean Theorem. Then dividing distance by speed will give us time, which is 200 seconds, or 3 minutes and 20 seconds.
Draw a right triangle with a height of 30,000 ft. and a base of 40,000 ft. The hypotenuse, or distance travelled, is then 50,000ft using the Pythagorean Theorem. Then dividing distance by speed will give us time, which is 200 seconds, or 3 minutes and 20 seconds.
A right triangle has two sides, 9 and x, and a hypotenuse of 15. What is x?
A right triangle has two sides, 9 and x, and a hypotenuse of 15. What is x?
Tap to see back →
We can use the Pythagorean Theorem to solve for x.
92 + _x_2 = 152
81 + _x_2 = 225
_x_2 = 144
x = 12
We can use the Pythagorean Theorem to solve for x.
92 + _x_2 = 152
81 + _x_2 = 225
_x_2 = 144
x = 12
Which set of sides could make a right triangle?
Which set of sides could make a right triangle?
Tap to see back →
By virtue of the Pythagorean Theorem, in a right triangle the sum of the squares of the smaller two sides equals the square of the largest side. Only 9, 12, and 15 fit this rule.
By virtue of the Pythagorean Theorem, in a right triangle the sum of the squares of the smaller two sides equals the square of the largest side. Only 9, 12, and 15 fit this rule.
A right triangle with a base of 12 and hypotenuse of 15 is shown below. Find x.

A right triangle with a base of 12 and hypotenuse of 15 is shown below. Find x.

Tap to see back →
Using the Pythagorean Theorem, the height of the right triangle is found to be = √(〖15〗2 –〖12〗2) = 9, so x=9 – 5=4
Using the Pythagorean Theorem, the height of the right triangle is found to be = √(〖15〗2 –〖12〗2) = 9, so x=9 – 5=4
A right triangle has sides of 36 and 39(hypotenuse). Find the length of the third side
A right triangle has sides of 36 and 39(hypotenuse). Find the length of the third side
Tap to see back →
use the pythagorean theorem:
a2 + b2 = c2 ; a and b are sides, c is the hypotenuse
a2 + 1296 = 1521
a2 = 225
a = 15
use the pythagorean theorem:
a2 + b2 = c2 ; a and b are sides, c is the hypotenuse
a2 + 1296 = 1521
a2 = 225
a = 15
A right triangle has one side equal to 5 and its hypotenuse equal to 14. Its third side is equal to:
A right triangle has one side equal to 5 and its hypotenuse equal to 14. Its third side is equal to:
Tap to see back →
The Pythagorean Theorem gives us _a_2 + _b_2 = _c_2 for a right triangle, where c is the hypotenuse and a and b are the smaller sides. Here a is equal to 5 and c is equal to 14, so _b_2 = 142 – 52 = 171. Therefore b is equal to the square root of 171 or approximately 13.07.
The Pythagorean Theorem gives us _a_2 + _b_2 = _c_2 for a right triangle, where c is the hypotenuse and a and b are the smaller sides. Here a is equal to 5 and c is equal to 14, so _b_2 = 142 – 52 = 171. Therefore b is equal to the square root of 171 or approximately 13.07.
Which of the following could NOT be the lengths of the sides of a right triangle?
Which of the following could NOT be the lengths of the sides of a right triangle?
Tap to see back →
We use the Pythagorean Theorem and we calculate that 25 + 49 is not equal to 100.
All of the other answer choices observe the theorem _a_2 + _b_2 = _c_2
We use the Pythagorean Theorem and we calculate that 25 + 49 is not equal to 100.
All of the other answer choices observe the theorem _a_2 + _b_2 = _c_2
The area of a right traingle is 42. One of the legs has a length of 12. What is the length of the other leg?
The area of a right traingle is 42. One of the legs has a length of 12. What is the length of the other leg?
Tap to see back →
Area= $\frac{1}{2}$times basetimes height
42=\frac{1}{2}$times basetimes 12
42=6times base
base=7
Area= $\frac{1}{2}$times basetimes height
42=\frac{1}{2}$times basetimes 12
42=6times base
base=7


If  and
and  , what is the length of
, what is the length of  ?
?

If 


Tap to see back →
AB is the leg adjacent to Angle A and BC is the leg opposite Angle A.
Since we have a  triangle, the opposites sides of those angles will be in the ratio
triangle, the opposites sides of those angles will be in the ratio  .
.
Here, we know the side opposite the sixty degree angle. Thus, we can set that value equal to  .
.




which also means

AB is the leg adjacent to Angle A and BC is the leg opposite Angle A.
Since we have a 

Here, we know the side opposite the sixty degree angle. Thus, we can set that value equal to 
which also means