How to find value with a number line - PSAT Math
Card 0 of 21

If the tick marks are equally spaced on the number line above, what is the average (arithmetic mean) of x, y, and z?
If the tick marks are equally spaced on the number line above, what is the average (arithmetic mean) of x, y, and z?
Tap to see back →
First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.
Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.
Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).
Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.
First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.
Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.
Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).
Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.
How many numbers 1 to 250 inclusive are cubes of integers?
How many numbers 1 to 250 inclusive are cubes of integers?
Tap to see back →
The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.
The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.

Refer to the above number line. Which of the points is most likely the location of the number  ?
?

Refer to the above number line. Which of the points is most likely the location of the number 
Tap to see back →
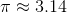 , so
, so 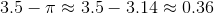
Therefore,

On the number line,  appears between 0.3 and 0.4 and is the correct choice.
appears between 0.3 and 0.4 and is the correct choice.
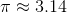
Therefore,
On the number line, 

If the tick marks are equally spaced on the number line above, what is the average (arithmetic mean) of x, y, and z?
If the tick marks are equally spaced on the number line above, what is the average (arithmetic mean) of x, y, and z?
Tap to see back →
First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.
Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.
Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).
Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.
First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.
Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.
Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).
Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.
How many numbers 1 to 250 inclusive are cubes of integers?
How many numbers 1 to 250 inclusive are cubes of integers?
Tap to see back →
The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.
The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.

Refer to the above number line. Which of the points is most likely the location of the number  ?
?

Refer to the above number line. Which of the points is most likely the location of the number 
Tap to see back →
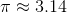 , so
, so 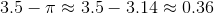
Therefore,

On the number line,  appears between 0.3 and 0.4 and is the correct choice.
appears between 0.3 and 0.4 and is the correct choice.
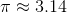
Therefore,
On the number line, 

If the tick marks are equally spaced on the number line above, what is the average (arithmetic mean) of x, y, and z?
If the tick marks are equally spaced on the number line above, what is the average (arithmetic mean) of x, y, and z?
Tap to see back →
First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.
Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.
Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).
Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.
First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.
Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.
Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).
Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.
How many numbers 1 to 250 inclusive are cubes of integers?
How many numbers 1 to 250 inclusive are cubes of integers?
Tap to see back →
The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.
The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.

Refer to the above number line. Which of the points is most likely the location of the number  ?
?

Refer to the above number line. Which of the points is most likely the location of the number 
Tap to see back →
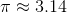 , so
, so 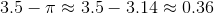
Therefore,

On the number line,  appears between 0.3 and 0.4 and is the correct choice.
appears between 0.3 and 0.4 and is the correct choice.
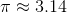
Therefore,
On the number line, 

If the tick marks are equally spaced on the number line above, what is the average (arithmetic mean) of x, y, and z?
If the tick marks are equally spaced on the number line above, what is the average (arithmetic mean) of x, y, and z?
Tap to see back →
First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.
Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.
Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).
Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.
First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.
Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.
Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).
Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.
How many numbers 1 to 250 inclusive are cubes of integers?
How many numbers 1 to 250 inclusive are cubes of integers?
Tap to see back →
The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.
The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.

Refer to the above number line. Which of the points is most likely the location of the number  ?
?

Refer to the above number line. Which of the points is most likely the location of the number 
Tap to see back →
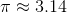 , so
, so 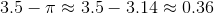
Therefore,

On the number line,  appears between 0.3 and 0.4 and is the correct choice.
appears between 0.3 and 0.4 and is the correct choice.
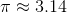
Therefore,
On the number line, 

If the tick marks are equally spaced on the number line above, what is the average (arithmetic mean) of x, y, and z?
If the tick marks are equally spaced on the number line above, what is the average (arithmetic mean) of x, y, and z?
Tap to see back →
First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.
Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.
Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).
Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.
First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.
Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.
Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).
Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.
How many numbers 1 to 250 inclusive are cubes of integers?
How many numbers 1 to 250 inclusive are cubes of integers?
Tap to see back →
The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.
The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.

Refer to the above number line. Which of the points is most likely the location of the number  ?
?

Refer to the above number line. Which of the points is most likely the location of the number 
Tap to see back →
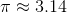 , so
, so 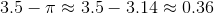
Therefore,

On the number line,  appears between 0.3 and 0.4 and is the correct choice.
appears between 0.3 and 0.4 and is the correct choice.
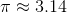
Therefore,
On the number line, 

If the tick marks are equally spaced on the number line above, what is the average (arithmetic mean) of x, y, and z?
If the tick marks are equally spaced on the number line above, what is the average (arithmetic mean) of x, y, and z?
Tap to see back →
First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.
Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.
Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).
Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.
First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.
Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.
Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).
Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.
How many numbers 1 to 250 inclusive are cubes of integers?
How many numbers 1 to 250 inclusive are cubes of integers?
Tap to see back →
The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.
The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.

Refer to the above number line. Which of the points is most likely the location of the number  ?
?

Refer to the above number line. Which of the points is most likely the location of the number 
Tap to see back →
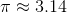 , so
, so 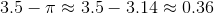
Therefore,

On the number line,  appears between 0.3 and 0.4 and is the correct choice.
appears between 0.3 and 0.4 and is the correct choice.
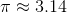
Therefore,
On the number line, 

If the tick marks are equally spaced on the number line above, what is the average (arithmetic mean) of x, y, and z?
If the tick marks are equally spaced on the number line above, what is the average (arithmetic mean) of x, y, and z?
Tap to see back →
First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.
Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.
Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).
Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.
First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.
Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.
Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).
Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.
How many numbers 1 to 250 inclusive are cubes of integers?
How many numbers 1 to 250 inclusive are cubes of integers?
Tap to see back →
The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.
The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.