How to multiply complex numbers - PSAT Math
Card 0 of 77
Which of the following is equal to 
?
Which of the following is equal to
Tap to see back →
, so 56 is a multiple of 4. 
raised to the power of any multiple of 4 is equal to 1, so
.
Multiply:
Multiply:
Tap to see back →
This is the product of a complex number and its complex conjugate. They can be multiplied using the pattern
with 
This is the product of a complex number and its complex conjugate. They can be multiplied using the pattern
with
Which of the following is equal to 
?
Which of the following is equal to
Tap to see back →
By the power of a product property,
By the power of a product property,
Which of the following is equal to 
?
Which of the following is equal to
Tap to see back →
The first step to solving this problem is distributing the exponent:
Next, we need simplify the complex portion.
Thus, our final answer is 
.
The first step to solving this problem is distributing the exponent:
Next, we need simplify the complex portion.
Thus, our final answer is
Simplify:
Simplify:
Tap to see back →
Use the FOIL method that states to multiply the Firsts, Outter, Inner, Lasts. Also remember that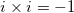 
:
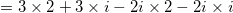
Use the FOIL method that states to multiply the Firsts, Outter, Inner, Lasts. Also remember that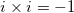
What is the eighth power of 
?
What is the eighth power of
Tap to see back →
First, square 
using the square of a binomial pattern as follows:
Raising this number to the fourth power yields the correct response:
First, square
Raising this number to the fourth power yields the correct response:
What is the eighth power of 
?
What is the eighth power of
Tap to see back →
raised to the power of any multiple of 4 is equal to 1, so the above expresion is equal to
This is not among the given choices.
This is not among the given choices.
What is the third power of 
?
What is the third power of
Tap to see back →
You are being asked to evaluate
You can use the cube of a binomial pattern with 
:
You are being asked to evaluate
You can use the cube of a binomial pattern with
What is the fourth power of 
?
What is the fourth power of
Tap to see back →
can be calculated by squaring 
, then squaring the result, using the square of a binomial pattern as follows:
Multiply 
by its complex conjugate. What is the product?
Multiply
Tap to see back →
The product of any complex number 
and its complex conjugate 
is the real number 
, so all that is needed here is to evaluate the expression:
The product of any complex number
What is the ninth power of 
?
What is the ninth power of
Tap to see back →
To raise a negative number to an odd power, take the absolute value of the base to that power and give its opposite:
To raise 
to a power, divide the power by 4 and raise 
to the remainder. Since
,
Therefore,
To raise a negative number to an odd power, take the absolute value of the base to that power and give its opposite:
To raise
Therefore,
Which of the following is equal to ?
Which of the following is equal to
Tap to see back →
, so 56 is a multiple of 4. raised to the power of any multiple of 4 is equal to 1, so
.
Multiply:
Multiply:
Tap to see back →
This is the product of a complex number and its complex conjugate. They can be multiplied using the pattern
with
This is the product of a complex number and its complex conjugate. They can be multiplied using the pattern
with
Which of the following is equal to ?
Which of the following is equal to
Tap to see back →
By the power of a product property,
By the power of a product property,
Which of the following is equal to ?
Which of the following is equal to
Tap to see back →
The first step to solving this problem is distributing the exponent:
Next, we need simplify the complex portion.
Thus, our final answer is .
The first step to solving this problem is distributing the exponent:
Next, we need simplify the complex portion.
Thus, our final answer is
Simplify:
Simplify:
Tap to see back →
Use the FOIL method that states to multiply the Firsts, Outter, Inner, Lasts. Also remember that :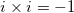
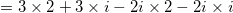
Use the FOIL method that states to multiply the Firsts, Outter, Inner, Lasts. Also remember that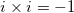
What is the eighth power of ?
What is the eighth power of
Tap to see back →
raised to the power of any multiple of 4 is equal to 1, so the above expresion is equal to
This is not among the given choices.
This is not among the given choices.
What is the third power of ?
What is the third power of
Tap to see back →
You are being asked to evaluate
You can use the cube of a binomial pattern with :
You are being asked to evaluate
You can use the cube of a binomial pattern with
What is the fourth power of ?
What is the fourth power of
Tap to see back →
can be calculated by squaring , then squaring the result, using the square of a binomial pattern as follows:
Multiply by its complex conjugate. What is the product?
Multiply
Tap to see back →
The product of any complex number and its complex conjugate is the real number , so all that is needed here is to evaluate the expression:
The product of any complex number