Triangles - PSAT Math
Card 0 of 1001
The ratio for the side lengths of a right triangle is 3:4:5. If the perimeter is 48, what is the area of the triangle?
The ratio for the side lengths of a right triangle is 3:4:5. If the perimeter is 48, what is the area of the triangle?
Tap to see back →
We can model the side lengths of the triangle as 3x, 4x, and 5x. We know that perimeter is 3x+4x+5x=48, which implies that x=4. This tells us that the legs of the right triangle are 3x=12 and 4x=16, therefore the area is A=1/2 bh=(1/2)(12)(16)=96.
We can model the side lengths of the triangle as 3x, 4x, and 5x. We know that perimeter is 3x+4x+5x=48, which implies that x=4. This tells us that the legs of the right triangle are 3x=12 and 4x=16, therefore the area is A=1/2 bh=(1/2)(12)(16)=96.
Jim leaves his home and walks 10 minutes due west and 5 minutes due south. If Jim could walk a straight line from his current position back to his house, how far, in minutes, is Jim from home?
Jim leaves his home and walks 10 minutes due west and 5 minutes due south. If Jim could walk a straight line from his current position back to his house, how far, in minutes, is Jim from home?
Tap to see back →
By using Pythagorean Theorem, we can solve for the distance “as the crow flies” from Jim to his home:
102 + 52 = _x_2
100 + 25 = _x_2
√125 = x, but we still need to factor the square root
√125 = √25*5, and since the √25 = 5, we can move that outside of the radical, so
5√5= x
By using Pythagorean Theorem, we can solve for the distance “as the crow flies” from Jim to his home:
102 + 52 = _x_2
100 + 25 = _x_2
√125 = x, but we still need to factor the square root
√125 = √25*5, and since the √25 = 5, we can move that outside of the radical, so
5√5= x
If one of the short sides of a 45-45-90 triangle equals 5, how long is the hypotenuse?
If one of the short sides of a 45-45-90 triangle equals 5, how long is the hypotenuse?
Tap to see back →
Using the Pythagorean theorem, _x_2 + _y_2 = _h_2. And since it is a 45-45-90 triangle the two short sides are equal. Therefore 52 + 52 = _h_2 . Multiplied out 25 + 25 = _h_2.
Therefore _h_2 = 50, so h = √50 = √2 * √25 or 5√2.
Using the Pythagorean theorem, _x_2 + _y_2 = _h_2. And since it is a 45-45-90 triangle the two short sides are equal. Therefore 52 + 52 = _h_2 . Multiplied out 25 + 25 = _h_2.
Therefore _h_2 = 50, so h = √50 = √2 * √25 or 5√2.
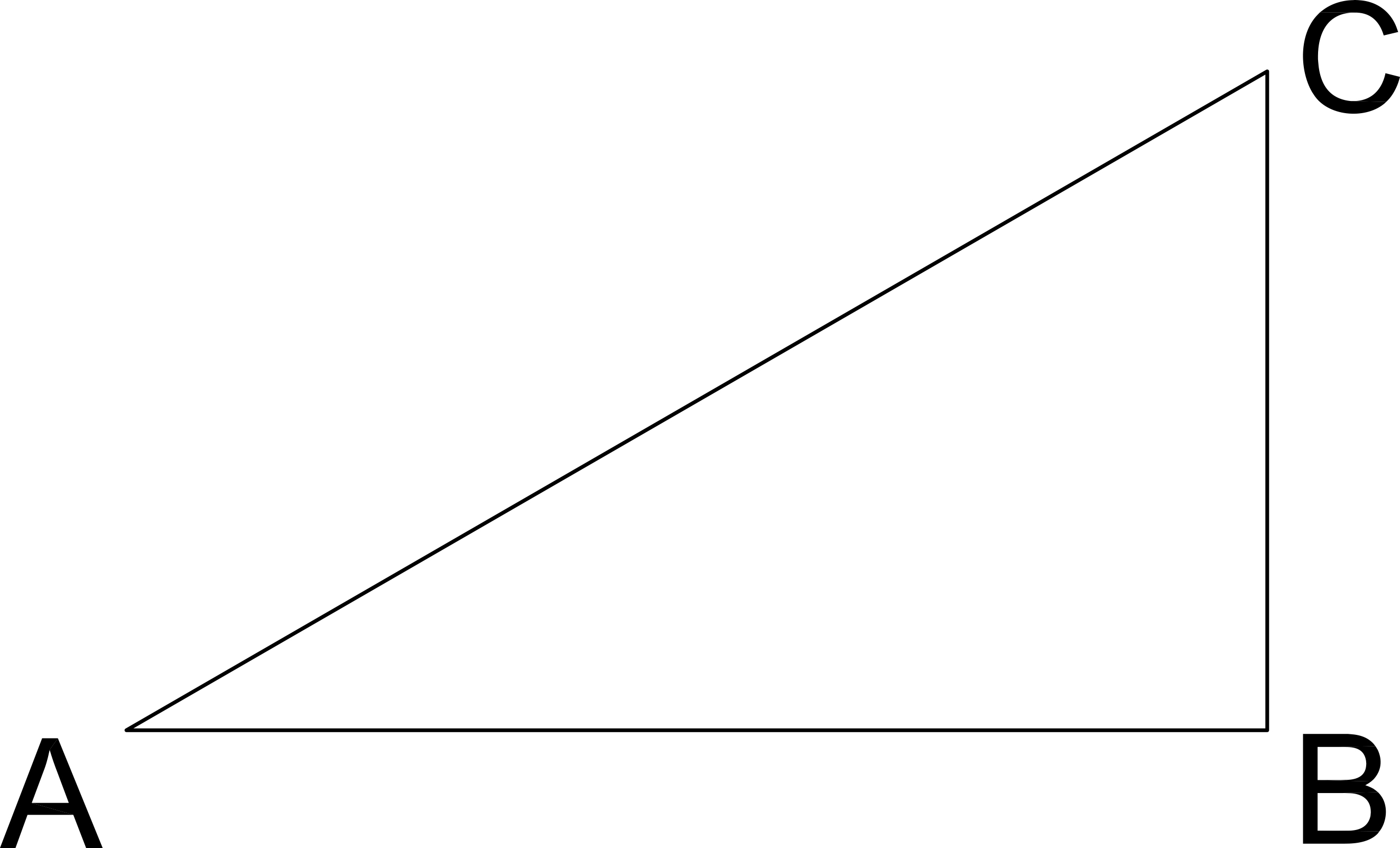
If the length of CB is 6 and the angle C measures 45º, what is the length of AC in the given right triangle?

If the length of CB is 6 and the angle C measures 45º, what is the length of AC in the given right triangle?
Tap to see back →
Pythagorean Theorum
AB2 + BC2 = AC2
If C is 45º then A is 45º, therefore AB = BC
AB2 + BC2 = AC2
62 + 62 = AC2
2*62 = AC2
AC = √(2*62) = 6√2
Pythagorean Theorum
AB2 + BC2 = AC2
If C is 45º then A is 45º, therefore AB = BC
AB2 + BC2 = AC2
62 + 62 = AC2
2*62 = AC2
AC = √(2*62) = 6√2
Bob the Helicopter is at 30,000 ft. above sea level, and as viewed on a map his airport is 40,000 ft. away. If Bob travels in a straight line to his airport at 250 feet per second, how many minutes will it take him to arrive?
Bob the Helicopter is at 30,000 ft. above sea level, and as viewed on a map his airport is 40,000 ft. away. If Bob travels in a straight line to his airport at 250 feet per second, how many minutes will it take him to arrive?
Tap to see back →
Draw a right triangle with a height of 30,000 ft. and a base of 40,000 ft. The hypotenuse, or distance travelled, is then 50,000ft using the Pythagorean Theorem. Then dividing distance by speed will give us time, which is 200 seconds, or 3 minutes and 20 seconds.
Draw a right triangle with a height of 30,000 ft. and a base of 40,000 ft. The hypotenuse, or distance travelled, is then 50,000ft using the Pythagorean Theorem. Then dividing distance by speed will give us time, which is 200 seconds, or 3 minutes and 20 seconds.
A right triangle has two sides, 9 and x, and a hypotenuse of 15. What is x?
A right triangle has two sides, 9 and x, and a hypotenuse of 15. What is x?
Tap to see back →
We can use the Pythagorean Theorem to solve for x.
92 + _x_2 = 152
81 + _x_2 = 225
_x_2 = 144
x = 12
We can use the Pythagorean Theorem to solve for x.
92 + _x_2 = 152
81 + _x_2 = 225
_x_2 = 144
x = 12
A triangle has sides of length 5, 7, and x. Which of the following can NOT be a value of x?
A triangle has sides of length 5, 7, and x. Which of the following can NOT be a value of x?
Tap to see back →
The sum of the lengths of any two sides of a triangle must exceed the length of the third side; therefore, 5+7 > x, which cannot happen if x = 13.
The sum of the lengths of any two sides of a triangle must exceed the length of the third side; therefore, 5+7 > x, which cannot happen if x = 13.
Two sides of a triangle have lengths 4 and 7. Which of the following represents the set of all possible lengths of the third side, x?
Two sides of a triangle have lengths 4 and 7. Which of the following represents the set of all possible lengths of the third side, x?
Tap to see back →
The set of possible lengths is: 7-4 < x < 7+4, or 3 < X < 11.
The set of possible lengths is: 7-4 < x < 7+4, or 3 < X < 11.
If two sides of a triangle have lengths 8 and 10, what could the length of the third side NOT be?
If two sides of a triangle have lengths 8 and 10, what could the length of the third side NOT be?
Tap to see back →
According to the Triangle Inequality Theorem, the sums of the lengths of any two sides of a triangle must be greater than the length of the third side. Since 10 + 8 is 18, the only length out of the answer choices that is not possible is 19.
According to the Triangle Inequality Theorem, the sums of the lengths of any two sides of a triangle must be greater than the length of the third side. Since 10 + 8 is 18, the only length out of the answer choices that is not possible is 19.
A square enclosure has a total area of 3,600 square feet. What is the length, in feet, of a diagonal across the field rounded to the nearest whole number?
A square enclosure has a total area of 3,600 square feet. What is the length, in feet, of a diagonal across the field rounded to the nearest whole number?
Tap to see back →
In order to find the length of the diagonal accross a square, we must first find the lengths of the individual sides.
The area of a square is found by multiply the lengths of 2 sides of a square by itself.
So, the square root of 3,600 comes out to 60 ft.
The diagonal of a square can be found by treating it like a right triangle, and so, we can use the pythagorean theorem for a right triangle.
602 + 602 = C2
the square root of 7,200 is 84.8, which can be rounded to 85
In order to find the length of the diagonal accross a square, we must first find the lengths of the individual sides.
The area of a square is found by multiply the lengths of 2 sides of a square by itself.
So, the square root of 3,600 comes out to 60 ft.
The diagonal of a square can be found by treating it like a right triangle, and so, we can use the pythagorean theorem for a right triangle.
602 + 602 = C2
the square root of 7,200 is 84.8, which can be rounded to 85
Dan drives 5 miles north and then 8 miles west to get to school. If he walks, he can take a direct path from his house to the school, cutting down the distance. How long is the path from Dan's house to his school?
Dan drives 5 miles north and then 8 miles west to get to school. If he walks, he can take a direct path from his house to the school, cutting down the distance. How long is the path from Dan's house to his school?
Tap to see back →
We are really looking for the hypotenuse of a triangle that has legs of 5 miles and 8 miles.
Apply the Pythagorean Theorem:
a2 + b2 = c2
25 + 64 = c2
89 = c2
c = 9.43 miles
We are really looking for the hypotenuse of a triangle that has legs of 5 miles and 8 miles.
Apply the Pythagorean Theorem:
a2 + b2 = c2
25 + 64 = c2
89 = c2
c = 9.43 miles
To get from his house to the hardware store, Bob must drive 3 miles to the east and then 4 miles to the north. If Bob was able to drive along a straight line directly connecting his house to the store, how far would he have to travel then?
To get from his house to the hardware store, Bob must drive 3 miles to the east and then 4 miles to the north. If Bob was able to drive along a straight line directly connecting his house to the store, how far would he have to travel then?
Tap to see back →
Since east and north directions are perpendicular, the possible routes Bob can take can be represented by a right triangle with sides a and b of length 3 miles and 5 miles, respectively. The hypotenuse c represents the straight line connecting his house to the store, and its length can be found using the Pythagorean theorem: _c_2 = 32+ 42 = 25. Since the square root of 25 is 5, the length of the hypotenuse is 5 miles.
Since east and north directions are perpendicular, the possible routes Bob can take can be represented by a right triangle with sides a and b of length 3 miles and 5 miles, respectively. The hypotenuse c represents the straight line connecting his house to the store, and its length can be found using the Pythagorean theorem: _c_2 = 32+ 42 = 25. Since the square root of 25 is 5, the length of the hypotenuse is 5 miles.
A right triangle has legs of 15m and 20m. What is the length of the hypotenuse?
A right triangle has legs of 15m and 20m. What is the length of the hypotenuse?
Tap to see back →
The Pythagorean theorem is a2 + b2 = c2, where a and b are legs of the right triangle, and c is the hypotenuse.
(15)2 + (20)2 = c2 so c2 = 625. Take the square root to get c = 25m
The Pythagorean theorem is a2 + b2 = c2, where a and b are legs of the right triangle, and c is the hypotenuse.
(15)2 + (20)2 = c2 so c2 = 625. Take the square root to get c = 25m
Acute angles x and y are inside a right triangle. If x is four less than one third of 21, what is y?
Acute angles x and y are inside a right triangle. If x is four less than one third of 21, what is y?
Tap to see back →
We know that the sum of all the angles must be 180 and we already know one angle is 90, leaving the sum of x and y to be 90.
Solve for x to find y.
One third of 21 is 7. Four less than 7 is 3. So if angle x is 3 then that leaves 87 for angle y.
We know that the sum of all the angles must be 180 and we already know one angle is 90, leaving the sum of x and y to be 90.
Solve for x to find y.
One third of 21 is 7. Four less than 7 is 3. So if angle x is 3 then that leaves 87 for angle y.
If the average (arithmetic mean) of two noncongruent angles of an isosceles triangle is  , which of the following is the measure of one of the angles of the triangle?
, which of the following is the measure of one of the angles of the triangle?
If the average (arithmetic mean) of two noncongruent angles of an isosceles triangle is 
Tap to see back →
Since the triangle is isosceles, we know that 2 of the angles (that sum up to 180) must be equal. The question states that the noncongruent angles average 55°, thus providing us with a system of two equations:


Solving for x and y by substitution, we get x = 70° and y = 40° (which average out to 55°).
70 + 70 + 40 equals 180 also checks out.
Since 70° is not an answer choice for us, we know that the 40° must be one of the angles.
Since the triangle is isosceles, we know that 2 of the angles (that sum up to 180) must be equal. The question states that the noncongruent angles average 55°, thus providing us with a system of two equations:
Solving for x and y by substitution, we get x = 70° and y = 40° (which average out to 55°).
70 + 70 + 40 equals 180 also checks out.
Since 70° is not an answer choice for us, we know that the 40° must be one of the angles.
Triangle ABC has angle measures as follows:
mangle ABC=4x+3
mangle ACB=2x+6
mangle BAC=3x
What is mangle BAC?
Triangle ABC has angle measures as follows:
mangle ABC=4x+3
mangle ACB=2x+6
mangle BAC=3x
What is mangle BAC?
Tap to see back →
The sum of the measures of the angles of a triangle is 180.
Thus we set up the equation 4x+3+2x+6+3x=180
After combining like terms and cancelling, we have 9x=171rightarrow x=19
Thus mangle BAC=3x=57
The sum of the measures of the angles of a triangle is 180.
Thus we set up the equation 4x+3+2x+6+3x=180
After combining like terms and cancelling, we have 9x=171rightarrow x=19
Thus mangle BAC=3x=57
The base angle of an isosceles triangle is $27^{circ}$. What is the vertex angle?
The base angle of an isosceles triangle is $27^{circ}$. What is the vertex angle?
Tap to see back →
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Solve the equation 27+27+x=180 for x to find the measure of the vertex angle.
x = 180 - 27 - 27
x = 126
Therefore the measure of the vertex angle is $126^{circ}$.
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Solve the equation 27+27+x=180 for x to find the measure of the vertex angle.
x = 180 - 27 - 27
x = 126
Therefore the measure of the vertex angle is $126^{circ}$.
The base angle of an isosceles triangle is five more than twice the vertex angle. What is the base angle?
The base angle of an isosceles triangle is five more than twice the vertex angle. What is the base angle?
Tap to see back →
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let x = the vertex angle and 2x+5 = the base angle
So the equation to solve becomes x+(2x+5)+(2x+5)=180
Thus the vertex angle is 34 and the base angles are 73.
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let x = the vertex angle and 2x+5 = the base angle
So the equation to solve becomes x+(2x+5)+(2x+5)=180
Thus the vertex angle is 34 and the base angles are 73.
If a right triangle has one leg with a length of 4 and a hypotenuse with a length of 8, what is the measure of the angle between the hypotenuse and its other leg?
If a right triangle has one leg with a length of 4 and a hypotenuse with a length of 8, what is the measure of the angle between the hypotenuse and its other leg?
Tap to see back →
The first thing to notice is that this is a 30o:60o:90o triangle. If you draw a diagram, it is easier to see that the angle that is asked for corresponds to the side with a length of 4. This will be the smallest angle. The correct answer is 30.
The first thing to notice is that this is a 30o:60o:90o triangle. If you draw a diagram, it is easier to see that the angle that is asked for corresponds to the side with a length of 4. This will be the smallest angle. The correct answer is 30.
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
Tap to see back →
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let  = vertex angle and
= vertex angle and  = base angle
= base angle
So the equation to solve becomes  .
.
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes 