Binomials - PSAT Math
Card 0 of 84
Solve for  .
.

Solve for 
Tap to see back →

Factor the expression
numerator: find two numbers that add to 2 and multiply to -8 \[use 4,-2\]
denominator: find two numbers that add to 5 and multiply to -14 \[use 7,-2\]
new expression:
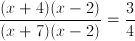
Cancel the 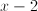 and cross multiply.
and cross multiply.



Factor the expression
numerator: find two numbers that add to 2 and multiply to -8 \[use 4,-2\]
denominator: find two numbers that add to 5 and multiply to -14 \[use 7,-2\]
new expression:
Cancel the 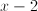
Multiply the binomial.
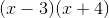
Multiply the binomial.
Tap to see back →
By multiplying with the foil method, we multiply our first values giving  , our outside values giving
, our outside values giving  . our inside values which gives
. our inside values which gives  , and out last values giving
, and out last values giving 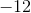 .
.
By multiplying with the foil method, we multiply our first values giving 


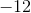
Give the coefficient of  in the binomial expansion of
in the binomial expansion of  .
.
Give the coefficient of 

Tap to see back →
If the expression  is expanded, then by the binomial theorem, the
is expanded, then by the binomial theorem, the  term is
term is


or, equivalently, the coefficient of  is
is

Therefore, the  coefficient can be determined by setting
coefficient can be determined by setting





If the expression 

or, equivalently, the coefficient of 
Therefore, the 
Give the coefficient of  in the binomial expansion of
in the binomial expansion of  .
.
Give the coefficient of 

Tap to see back →
If the expression  is expanded, then by the binomial theorem, the
is expanded, then by the binomial theorem, the  term is
term is


or, equivalently, the coefficient of  is
is

Therefore, the  coefficient can be determined by setting
coefficient can be determined by setting
 :
:




If the expression 

or, equivalently, the coefficient of 
Therefore, the 

Give the coefficient of  in the product
in the product
 .
.
Give the coefficient of 

Tap to see back →
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two  terms and one constant are multiplied; find the three products and add them, as follows:
terms and one constant are multiplied; find the three products and add them, as follows:






Add:  .
.
The correct response is  .
.
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two 
Add: 
The correct response is 
Give the coefficient of  in the product
in the product
 .
.
Give the coefficient of 

Tap to see back →
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two  terms and one constant are multiplied; find the three products and add them, as follows:
terms and one constant are multiplied; find the three products and add them, as follows:






Add: 
The correct response is -122.
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two 
Add:
The correct response is -122.
Give the coefficient of  in the product
in the product

Give the coefficient of 
Tap to see back →
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two  terms and one constant are multiplied; find the three products and add them, as follows:
terms and one constant are multiplied; find the three products and add them, as follows:






Add: 
The correct response is  .
.
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two 
Add:
The correct response is 
Give the coefficient of  in the binomial expansion of
in the binomial expansion of  .
.
Give the coefficient of 

Tap to see back →
If the expression  is expanded, then by the binomial theorem, the
is expanded, then by the binomial theorem, the  term is
term is


or, equivalently, the coefficient of  is
is

Therefore, the  coefficient can be determined by setting
coefficient can be determined by setting
 :
:




If the expression 

or, equivalently, the coefficient of 
Therefore, the 

Decrease  by 40%. Which of the following will this be equal to?
by 40%. Which of the following will this be equal to?
Decrease 
Tap to see back →
A number decreased by 40% is equivalent to 100% of the number minus 40% of the number. This is taking 60% of the number, or, equivalently, multiplying it by 0.6.
Therefore,  decreased by 40% is 0.6 times this, or
decreased by 40% is 0.6 times this, or

A number decreased by 40% is equivalent to 100% of the number minus 40% of the number. This is taking 60% of the number, or, equivalently, multiplying it by 0.6.
Therefore, 
Find the product:

Find the product:
Tap to see back →
Find the product:

Use the distributive property:


Write the resulting expression in standard form:

Find the product:
Use the distributive property:
Write the resulting expression in standard form:
If 〖(x+y)〗2 = 144 and 〖(x-y)〗2 = 64, what is the value of xy?
If 〖(x+y)〗2 = 144 and 〖(x-y)〗2 = 64, what is the value of xy?
Tap to see back →
We first expand each binomial to get x2 + 2xy + y2 = 144 and x2 - 2xy + y2 = 64. We then subtract the second equation from the first to find 4xy = 80. Finally, we divide each side by 4 to find xy = 20.
We first expand each binomial to get x2 + 2xy + y2 = 144 and x2 - 2xy + y2 = 64. We then subtract the second equation from the first to find 4xy = 80. Finally, we divide each side by 4 to find xy = 20.
Which of these expressions can be simplified further by collecting like terms?
Which of these expressions can be simplified further by collecting like terms?
Tap to see back →
A binomial can be simplified further if and only if the two terms have the same combination of variables and the same exponents for each like variable. This is not the case in any of the four binomials given, so none of the expressions can be simplified further.
A binomial can be simplified further if and only if the two terms have the same combination of variables and the same exponents for each like variable. This is not the case in any of the four binomials given, so none of the expressions can be simplified further.
Solve for  .
.

Solve for 
Tap to see back →

Factor the expression
numerator: find two numbers that add to 2 and multiply to -8 \[use 4,-2\]
denominator: find two numbers that add to 5 and multiply to -14 \[use 7,-2\]
new expression:
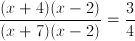
Cancel the 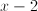 and cross multiply.
and cross multiply.



Factor the expression
numerator: find two numbers that add to 2 and multiply to -8 \[use 4,-2\]
denominator: find two numbers that add to 5 and multiply to -14 \[use 7,-2\]
new expression:
Cancel the 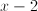
Multiply the binomial.
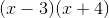
Multiply the binomial.
Tap to see back →
By multiplying with the foil method, we multiply our first values giving  , our outside values giving
, our outside values giving  . our inside values which gives
. our inside values which gives  , and out last values giving
, and out last values giving 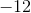 .
.
By multiplying with the foil method, we multiply our first values giving 


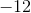
Give the coefficient of  in the binomial expansion of
in the binomial expansion of  .
.
Give the coefficient of 

Tap to see back →
If the expression  is expanded, then by the binomial theorem, the
is expanded, then by the binomial theorem, the  term is
term is


or, equivalently, the coefficient of  is
is

Therefore, the  coefficient can be determined by setting
coefficient can be determined by setting





If the expression 

or, equivalently, the coefficient of 
Therefore, the 
Give the coefficient of  in the binomial expansion of
in the binomial expansion of  .
.
Give the coefficient of 

Tap to see back →
If the expression  is expanded, then by the binomial theorem, the
is expanded, then by the binomial theorem, the  term is
term is


or, equivalently, the coefficient of  is
is

Therefore, the  coefficient can be determined by setting
coefficient can be determined by setting
 :
:




If the expression 

or, equivalently, the coefficient of 
Therefore, the 

Give the coefficient of  in the product
in the product
 .
.
Give the coefficient of 

Tap to see back →
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two  terms and one constant are multiplied; find the three products and add them, as follows:
terms and one constant are multiplied; find the three products and add them, as follows:






Add:  .
.
The correct response is  .
.
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two 
Add: 
The correct response is 
Give the coefficient of  in the product
in the product
 .
.
Give the coefficient of 

Tap to see back →
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two  terms and one constant are multiplied; find the three products and add them, as follows:
terms and one constant are multiplied; find the three products and add them, as follows:






Add: 
The correct response is -122.
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two 
Add:
The correct response is -122.
Give the coefficient of  in the product
in the product

Give the coefficient of 
Tap to see back →
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two  terms and one constant are multiplied; find the three products and add them, as follows:
terms and one constant are multiplied; find the three products and add them, as follows:






Add: 
The correct response is  .
.
While this problem can be answered by multiplying the three binomials, it is not necessary. There are three ways to multiply one term from each binomial such that two 
Add:
The correct response is 
Give the coefficient of  in the binomial expansion of
in the binomial expansion of  .
.
Give the coefficient of 

Tap to see back →
If the expression  is expanded, then by the binomial theorem, the
is expanded, then by the binomial theorem, the  term is
term is


or, equivalently, the coefficient of  is
is

Therefore, the  coefficient can be determined by setting
coefficient can be determined by setting
 :
:




If the expression 

or, equivalently, the coefficient of 
Therefore, the 
